Tables and Shares – Complete Guide For Class 4 Math Chapter 11

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Tables and Shares in Mathematics for Class 4th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

Students are introduced to multiplication and division concepts and their practical applications in everyday circumstances in the chapter “Tables and Shares.” It focuses on viewing division as the act of equitably dividing or grouping and multiplication as the action of repeated addition. By examining tables and identifying patterns in numbers, the chapter helps students improve their fundamental arithmetic abilities.

Students gain efficient problem-solving skills by using multiplication tables through interesting examples and word problems. Additionally, they investigate the idea of distributing things evenly among groups, which promotes an awareness of differences. By requiring students to solve problems involving the equitable division of amounts or the sharing of objects, the chapter “Tables And Shares” promotes critical thinking skills.

“Tables and Shares” aims to build a strong foundation for further mathematical learning, enhancing problem-solving abilities and reinforcing the importance of arithmetic operations in everyday life. The chapter also integrates hands-on activities, allowing students to practice and visualize mathematical operations, making the learning experience more interactive and engaging.

Key Concepts

There are various key concepts discussed in the chapter “Tables and Shares”. These include

1. Multiplication as Repeated Addition Multiplication is the repeated addition of the same number. For Example, multiplying 4 by 3 means adding 4 three times:
   4 + 4 + 4 = 12
   This gives us the same result as:
   4 × 3 = 12
   
   Example:
   Suppose we have 5 baskets, and each basket contains 6 apples. To find the total number of apples, we can use repeated addition:
   6 + 6 + 6 + 6 + 6 = 30
   Or, we can use multiplication:
   5 × 6 = 30
   So, there are 30 apples in total.
   
2. Understanding Division as Equal Sharing: Division is the process of sharing or grouping numbers into equal parts. It is the inverse of multiplication. For example, if you have 12 apples and you want to divide them equally among 4 friends, you are performing a division operation:
   12 ÷ 4 = 3
   Each friend will get 3 apples.
   
   Example:
   Suppose there are 20 candies, and they need to be shared equally among 5 children. We divide the total number of candies by the number of children:
   20 ÷ 5 = 4
   Each child will receive 4 candies.
   
3. Relationship Between Multiplication and Division: Division and multiplication have a close relationship. Understanding the connection facilitates students’ smooth transition from one task to another. For example, if you know that:
   5 × 4 = 20
   Then you also know that:
   20 ÷ 4 = 5 and 20 ÷ 5 = 4
   
4. Using Multiplication Tables A useful resource for solving division and multiplication problems is a table of multiplication. This chapter’s key component is teaching students tables up to 10, which will enable them to answer problems more quickly. For example, if a student knows the table of 7, they can quickly find the result of:
   7 × 6 = 42
   Multiplication tables also assist in division problems. If a student knows that:
   6 × 4 = 24
   Then they can easily deduce that:
   24 ÷ 6 = 4 and 24 ÷ 4 = 6
   
5. Practical Examples and Word Problems: This chapter “Tables And Shares” encourages students to apply the concepts of multiplication and division in real-life situations through word problems.
   
   Example 1:
   A farmer has 24 eggs, and he wants to pack them into cartons with 6 eggs in each carton. How many cartons can he fill?
   Solution: We divide the total number of eggs by the number of eggs per carton:
   24 ÷ 6 = 4
   So, the farmer can fill 4 cartons.
   
   Example 2:
   A teacher has 32 pencils, and she wants to give 8 pencils to each student. How many students will receive pencils?
   Solution: We divide the total number of pencils by the number of pencils per student:
   32 ÷ 8 = 4
   So, 4 students will receive pencils.
   
6. Understanding Grouping: Division can also be understood as grouping. Instead of sharing, students can group objects to form sets of equal sizes.
   
   Example:
   Suppose there are 15 marbles, and you want to make groups of 5 marbles each. How many groups can you form?
   You divide the total number of marbles by the number of marbles in each group:
   15 ÷ 5 = 3
   So, you can make 3 groups of 5 marbles each.

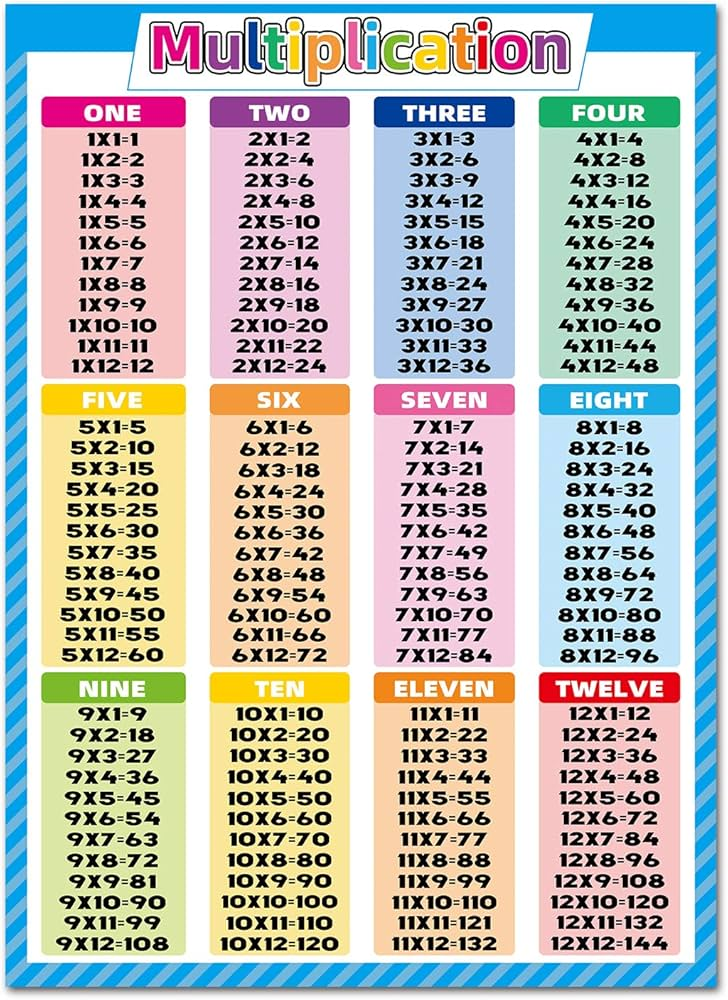
When adding the same number more than once, multiplication is a fundamental mathematical process that makes it easier for us to rapidly determine the total. It’s a more direct method of expressing “repeated addition.”

Types Of Multiplication

Let’s explore the two types of multiplication mentioned in the chapter “Tables and Shares”:

1. Multiplying a one-digit number by a one-digit number
2. Multiplying a two-digit number by a one-digit number

We will explain each with practical, easy-to-understand examples.

1. Multiplication of a One-Digit Number by a One-Digit Number

Multiplication of smaller numbers, like 3 times 4 or 5 times 2, is essentially adding the same number multiple times.

Example:
Let’s say you have 4 baskets, and each basket has 3 oranges. How many oranges do you have in total?

Instead of adding 3 + 3 + 3 + 3, we can multiply:

4 × 3 = 12

So, there are 12 oranges in total.

Multiplication makes this process faster by telling you that if you have 4 groups of 3, the total is 12. This is called repeated addition.

Another Example:

Imagine you have 5 plates, and each plate has 2 cookies. How many cookies do you have?

Instead of adding 2 + 2 + 2 + 2 + 2, you can multiply:

5 × 2 = 10

So, there are 10 cookies in total.

2. Multiplication of a Two-Digit Number by a One-Digit Number

Now, let’s move to slightly bigger numbers. Here, we multiply a number like 12 or 24 by a smaller number like 3 or 5.

Example:
You have 12 pencils in each box, and there are 3 boxes. How many pencils do you have in total?

We multiply the number of pencils per box by the number of boxes:

12 × 3 = 36

So, there are 36 pencils in total.

Another Example:

You have 24 apples in each basket, and there are 2 baskets. How many apples are there altogether?

We multiply the number of apples per basket by the number of baskets:

24 × 2 = 48

So, there are 48 apples in total.

Step-by-Step Process for Multiplying Two-Digit Numbers by One-Digit Numbers:

1. Multiply the digits:
   Take the digits one at a time and multiply them by the one-digit number. For example, in 12 × 3, first multiply the one’s place digit (2 × 3 = 6), and then multiply the tens place digit (1 × 3 = 3).
2. Combine the results:
   The result is 36. So, 12 × 3 = 36.

Visualizing Multiplication

As per the chapter Tables and Shares, To help understand multiplication, students can use objects like marbles, pencils, or toys. Let’s take the example of 3 plates with 4 candies on each plate.

• Draw 3 plates on the board or use real objects.
• Place 4 candies on each plate.
• Now count how many candies there are in total. You’ll see there are 12 candies.

This is 3 × 4 = 12, showing how multiplication works in a visual way.

Practical Applications of Multiplication

Multiplication is useful in everyday life. Here are some situations where you might use multiplication:

• Counting items: If you have 5 bags with 6 apples in each, multiplying helps you find the total number of apples.
• Shopping: If each pen costs ₹10, and you buy 4 pens, you can multiply to find the total cost: 4 × 10 = ₹40.

Activity: “Sharing Apples”

This activity will help students practice both multiplication and division through a fun, hands-on approach.

Materials:

• A set of 24 paper apples (or use real apples if possible)
• 6 small baskets
• A marker and paper to write numbers

Instructions:

1. Introduction: Inform students that they are going to help a farmer distribute apples to his workers. The farmer wishes to distribute his twenty-four apples equally among his six employees.
2. Step 1 – Division as Sharing:
   Start by explaining that division implies equitable sharing of resources. When the 24 apples are divided among 6 workers, ask students how many apples each worker will receive. After giving it an attempt at solving it, explain:

24 ÷ 6 = 4
So, each worker will get 4 apples.

3. Step 2 – Hands-on Division:
   Give the students the paper apples and instruct them to put four apples in each basket until all the apples have been distributed. After they’re finished, have them determine how many apples are in each basket. Repeat the idea that sharing is equal in division.
4. Step 3 – Multiplication to Check:
   Now, let’s check if the division is correct by using multiplication. Ask the students to multiply the number of apples in one basket by the total number of baskets:
   4 × 6 = 24
   This confirms that the division was done correctly.
5. Step 4 – Explore Grouping:
   Next, ask the students to group the apples in sets of 4 and figure out how many groups they can make. Explain that this is another way of understanding division, by grouping instead of sharing. They should come up with the same result:
   24 ÷ 4 = 6
   So, they can make 6 groups of 4 apples each.

Division is one of the four basic mathematical operations, and it’s all about sharing or grouping things equally. When we divide, we are essentially splitting a number into smaller, equal parts.

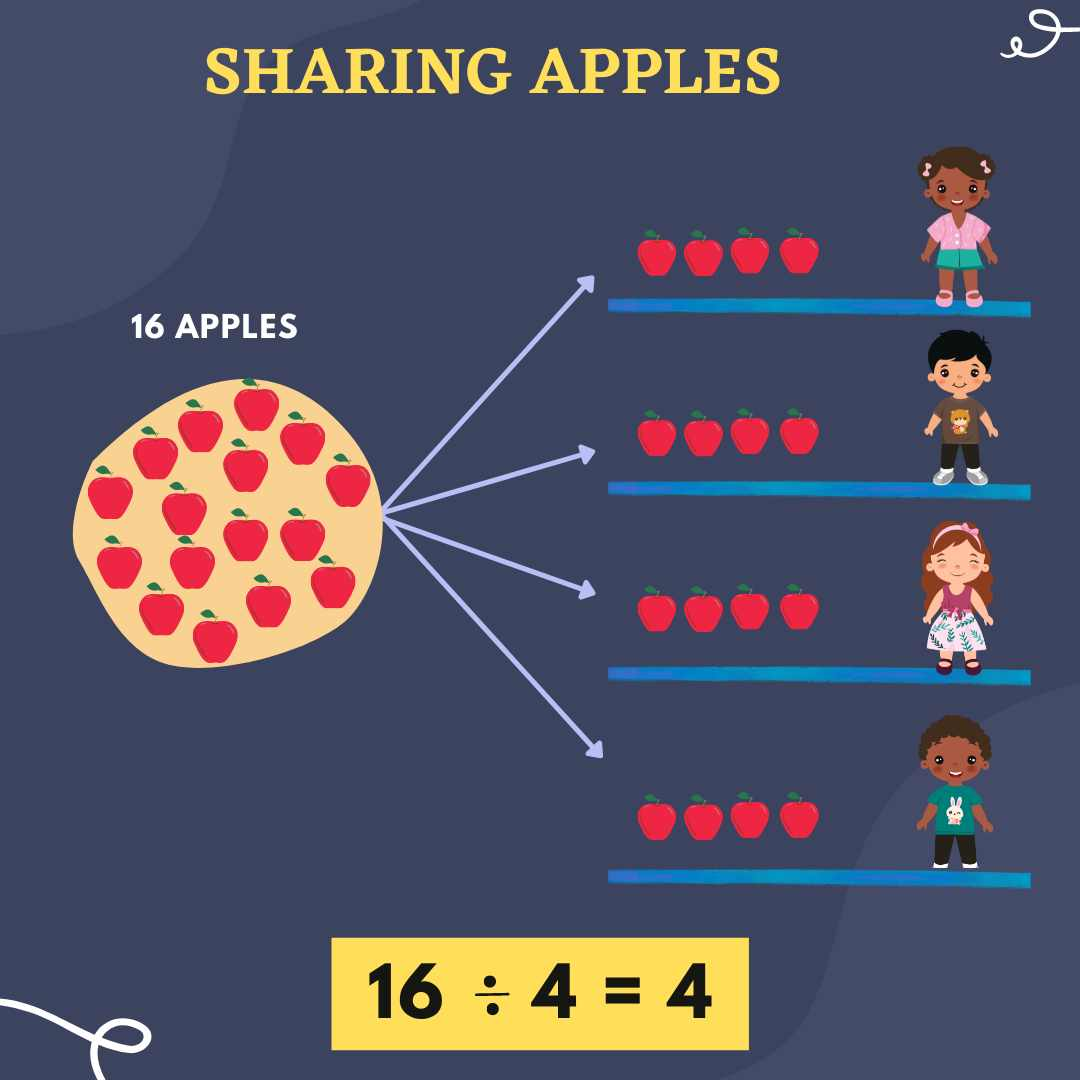
Types Of Division

Let’s explore two types of division that Class 4 students will learn:

1. Dividing a one-digit number by a one-digit number
2. Dividing a two-digit number by a one-digit number

We’ll explain each type with simple, practical examples that are easy to understand.

1. Division of a One-Digit Number by a One-Digit Number

This is when we divide a small number (like 8 or 6) by another small number (like 2 or 3). Think of this as sharing a few objects equally among a few people.

Example:
Let’s say you have 6 chocolates, and you want to share them equally among 2 friends. How many chocolates will each friend get?

To solve this, we divide 6 by 2:

6 ÷ 2 = 3

This means each friend will get 3 chocolates. So, division is like sharing chocolates equally among your friends.

Another Example:

Suppose you have 8 pencils, and you want to give them to 4 classmates equally. How many pencils will each classmate get?

We divide 8 by 4:

8 ÷ 4 = 2

So, each classmate will get 2 pencils.

2. Division of a Two-Digit Number by a One-Digit Number

Now, let’s move on to bigger numbers. This is when we divide a larger number (like 24 or 36) by a smaller number (like 3 or 6). The process is the same, but it takes a bit more time.

Example:
Imagine you have 24 apples, and you want to pack them into bags, with 6 apples in each bag. How many bags will you need?

We divide 24 by 6:

24 ÷ 6 = 4

This means you will need 4 bags to pack all the apples.

Another Example:

You have 36 marbles, and you want to share them equally among 4 friends. How many marbles will each friend get?

We divide 36 by 4:

36 ÷ 4 = 9

So, each friend will get 9 marbles.

Step-by-Step Process for Division of Two-Digit Numbers:

1. Look at the first digit:
   Take the first digit of the two-digit number and see if you can divide it by the divisor. For example, in 24 ÷ 6, we look at the whole number 24 because it’s less than 10.
2. Divide it:
   Divide the number by the divisor. In this case, 24 ÷ 6 equals 4.
3. Write the answer:
   The answer (or quotient) is how many groups we can make or how many each person will get. So, for 24 ÷ 6, the answer is 4.

Visualizing Division

To make division easier to understand, you can use objects like pencils, marbles, or even pieces of paper. Let’s take the example of 24 apples being divided into groups of 6 apples.

• Draw 24 apples on the board or use 24 small objects.
• Now, group them into sets of 6.
• Count how many groups you made. You’ll see there are 4 groups.

This visual method helps students understand the concept of grouping in division.

Conclusion

In conclusion, CBSE Class 4th Math, Chapter 11 – Tables and Shares equips students with essential arithmetic skills through engaging methods and practical applications. The chapter “Tables And Shares” not only simplifies the concepts of multiplication and division but also emphasizes their real-life relevance, making learning both effective and enjoyable.

By mastering the techniques of multiplication as repeated addition and understanding division as equal sharing, students develop a strong foundation that is crucial for their mathematical journey. The hands-on activities, relatable examples, and the exploration of types of multiplication and division further enrich their learning experience, fostering critical thinking and problem-solving skills.

As students progress through CBSE Class 4th Math, Chapter 11 – Tables and Shares, they not only learn to perform calculations but also appreciate the beauty and utility of mathematics in everyday situations. With the right resources and a clear understanding of these concepts, they are well-prepared to tackle more complex mathematical challenges in the future. Let’s continue to explore and enjoy the fascinating world of mathematics together!