Perimeter and Area – Complete Guide For Class 6th Math Chapter 6
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Perimeter and Area in Mathematics for Class 6th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.
The chapter Perimeter and Area introduces students to the fundamental concepts of measuring the boundaries and enclosed spaces of various shapes. The perimeter is defined as the total length around a figure, such as a rectangle, square, or any polygon, calculated by summing the lengths of all its sides. The area, on the other hand, measures the space within a closed figure and is typically expressed in square units. Through practical examples and activities, students develop a solid understanding of how to apply these concepts to solve real-world problems, laying the groundwork for more advanced geometric studies.
Perimeter and Area
Perimeter
The perimeter of any closed plane figure is the total distance covered along its boundary when you trace around it once.
For polygons, which are closed plane figures made up of straight line segments, the perimeter is simply the sum of the lengths of all its sides.
Perimeter Formulas for Common Shapes
Perimeter of Rectangle
As stated in the chapter perimeter and area, the perimeter of a rectangle is calculated by adding together the lengths of all four sides. A simpler formula is to double the sum of the rectangle’s length and breadth:
Perimeter of a rectangle = 2 × (length + breadth)
For example, if a rectangle has a length of 12 cm and a breadth of 8 cm, its perimeter would be 40 cm.
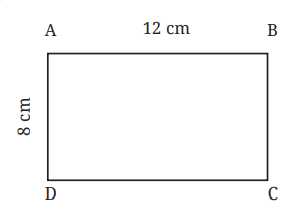
Perimeter of rectangle = Sum of the lengths of its four sides
= AB + BC + CD + DA
= AB + BC + AB + BC
= 2 × AB + 2 × BC
= 2 × (AB + BC)
= 2 × (12 cm + 8 cm)
= 2 × (20 cm) = 40 cm.
From this example, we see that the perimeter of a rectangle = length + breadth + length + breadth.
The perimeter of a rectangle = 2 × (length + breadth).
The perimeter of a rectangle is twice the sum of its length and breadth.
Perimeter of Square
As mentioned in the chapter perimeter and area, Since all four sides of a square are equal, the perimeter is four times the length of one side:
The perimeter of a square = 4 × length of a side
For instance, a square with a side length of 1 meter would have a perimeter of 4 meters.
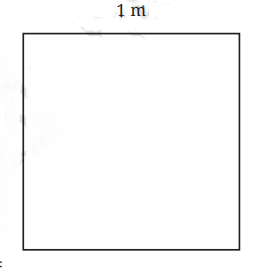
The perimeter of the square = sum of the lengths of all four sides of the square
= 1 m + 1 m + 1 m + 1 m = 4 m.
Now, we know that all four sides of a square are equal in length.
Therefore, in place of adding the lengths of each side, we can simply multiply the length of one side by 4.
Thus, the length of the tape required = 4 × 1 m = 4 m.
From this example, we see that the Perimeter of a square = 4 × length of a side.
The perimeter of a square is quadruple the length of its side.
The Perimeter of a Triangle
The chapter perimeter and area also cover The perimeter of a triangle, which is the sum of the lengths of its three sides.
For example, Consider a triangle having three given sides of lengths 4 cm, 5 cm and 7 cm. Find its perimeter.
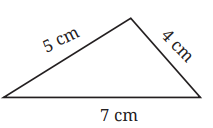
The perimeter of the triangle = 4 cm + 5 cm + 7 cm = 16 cm.
The perimeter of a triangle is = sum of the lengths of its three sides
Practical Examples of Common Shapes
Example 1: Akshi wants to put lace around a rectangular tablecloth that is 3 meters long and 2 meters wide.
Solution: Length of the rectangular table cover = 3 m.
The breadth of the rectangular table cover = 2 m.
Akshi wants to put lace all around the tablecloth.
Therefore, the length of the lace required will be the perimeter of the rectangular tablecloth.
Now, the perimeter of the rectangular tablecloth = 2 × (length + breadth) = 2 × (3 m + 2 m) = 2 × 5 m = 10 m.
Hence, the length of the lace required is 10 m.
Example 2: Usha takes three rounds of a square park with each side measuring 75 meters.
Solution:
Perimeter of the square park = 4 × length of a side = 4 × 75 m = 300 m. Distance covered by Usha in one round = 300 m.
Therefore, the total distance traveled by Usha in three rounds = 3 × 300 m = 900 m.
Deep Dive Activity
Understanding Perimeters through Real-Life Applications
In races, tracks often share a common finish line.
Imagine two square tracks: the inner track has sides of 100 meters, while the outer track has sides of 150 meters.
If the race is 350 meters long, where should the starting positions be to ensure both runners finish at the same point? This type of problem helps students apply perimeter concepts to real-world situations.
Explore and Verify
To better understand perimeter, try this activity:
Take a piece of paper, cut it into different shapes, and estimate the perimeter. Then, measure the actual perimeter with a scale or tape measure to see how close your estimation was.
Perimeter of Regular Polygons
Regular polygons are closed figures with all sides and angles equal, like equilateral triangles or regular pentagons.
The perimeter of a regular polygon is the length of one side multiplied by the number of sides.
Perimeter of Equilateral Triangle
We know that for any triangle its perimeter is sum of all three sides.
Using this understanding, we can find the perimeter of an equilateral triangle.

Perimeter of an equilateral triangle = AB + BC + AC
= AB + AB + AB (all sides are equal)
= 3 times length of one side.
Perimeter of an equilateral triangle = 3 × length of a side
Understanding Area
The chapter perimeter and area covers a deep understanding of the concept of Area. This involves-
Area
The area of a closed figure is the amount of region enclosed within its boundaries. This concept was introduced in earlier grades using square grid paper.
Area of a Rectangle
Area = length × width
Area of a Square
Area = side length × side length
Example 1: A floor is 5 m long and 4 m wide. A square carpet of sides 3 m is laid on the floor. Find the area of the floor that is not carpeted.
Solution
Length of the floor = 5 m.
Width of the floor = 4 m.
Area of the floor = length × width = 5 m × 4 m = 20 sq m.
Length of the square carpet = 3 m.
Area of the carpet = length × length = 3 m × 3 m = 9 sq m.
Hence, the area of the floor laid with carpet is 9 sq m.
Area of the floor that is not carpeted is = area of the floor – the area of the floor laid with carpet
= 20 sq m – 9 sq m
= 11 sq m.
Example 2: Four square flower beds each of side 4 m are in four corners on a piece of land 12 m long and 10 m wide. Find the area of the remaining part of the land.
Solution:
Length of the land (l) = 12 m.
Width of land (w) = 10 m.
Area of the whole land = l × w = 12 m × 10 m = 120 sq m.
The sidelength of each of the four square flower beds is (s) = 4 m.
Area of one flower bed = s × s = 4 m × 4 m = 16 sq m.
Hence, the area of the four flower beds = 4 × 16 sq m = 64 sq m.
Area of the remaining part of the land = area of the complete land – the area of all four flower beds
= 120 sq m – 64 sq m
= 56 sq m.
Estimating Area Using Graph Paper
The chapter perimeter and area also covers estimating area using graph paper. You can estimate the area of any simple closed shape using graph paper by counting the full squares and appropriately accounting for partial squares.
Look at the figures below and guess which one of them has a larger area.
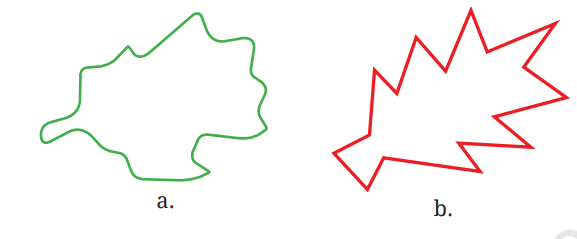
We can estimate the area of any simple closed shape by using a sheet of squared paper or graph paper where every square measures 1 unit × 1 unit or 1 square unit.
To estimate the area, we can trace the shape onto a piece of transparent paper and place the same on a piece of squared or graph paper and then follow the below conventions—
1. The area of one full small square of the squared or graph paper is taken as 1 sq unit.
2. Ignore portions of the area that are less than half a square.
3. If more than half of a square is in a region, just count it as 1 sq unit.
Area of a Triangle
The chapter Perimeter and area covers the area of a triangle. It includes-
Understanding Triangle Area
Activity: Cut a rectangle along its diagonal to form two triangles.
Notice that these triangles have the same area, indicating that the area of each triangle is half the area of the rectangle.
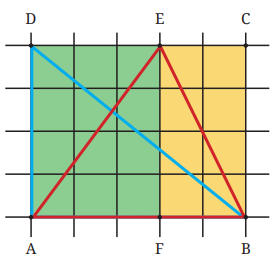
Formula: Area of a Triangle: For any triangle formed by drawing a diagonal in a rectangle, the area of the triangle is half the area of the rectangle.
Find the Area of triangle ABE?
Solution:
The area of triangle BAD is half of the area of the rectangle ABCD.
Area of triangle ABE = Area of triangle AEF + Area of triangle BEF.
Here, the area of triangle AEF = half of the area of rectangle AFED.
Similarly, the area of triangle BEF = half of the area of rectangle BFEC.
Thus, the area of triangle ABE = half of the area of rectangle AFED +half of the area of rectangle BFEC.
= half of the sum of the areas of the rectangles AFED and BFEC
= half of the area of the rectangle ABCD.
Perimeter and Area Relationship
Perimeter: The sum of all the sides of a polygon.
Area: The measure of the enclosed space.
Key Insight: Two shapes can have the same area but different perimeters, or the same perimeter but different areas.
Let’s Conclude
In summary, CBSE Class 6th Math, Chapter 6 – Perimeter and Area equips students with essential skills to measure and understand both the boundaries and the spaces within various shapes. The chapter on Perimeter and Area provides clear explanations of how to calculate the perimeter of rectangles, squares, and triangles, alongside real-life applications and practical examples. Similarly, the section on Area delves into methods for finding the area of rectangles, squares, and triangles, enhancing students’ ability to apply these concepts in everyday situations.
Through engaging activities, such as estimating perimeter and areas with graph paper and practical problems like measuring lace around a tablecloth or calculating distances in a park, students gain a comprehensive grasp of the concepts. The relationship between perimeter and area further reinforces the understanding that while two shapes can share the same area, their perimeters might differ, and vice versa. By mastering these principles, students are well-prepared for more advanced mathematical concepts and applications.
The chapter Perimeter and Area is a foundational element of geometry that helps bridge the gap between basic and more complex geometric studies. Remember, the chapter Perimeter and Area not only builds mathematical skills but also encourages students to appreciate the practical uses of geometry in the real world.
Practice questions on Chapter 6 - Perimeter And Area
Get your free Chapter 6 - Perimeter And Area practice quiz of 20+ questions & detailed solutions
Practice Now