Mechanical Properties of Solids – Complete Guide for Class 11 Physics Chapter 9
Welcome to iPrep, your Learning Super App. Our learning resources for Chapter 9, “Mechanical Properties of Solids,” in Class 11 Physics are meticulously designed to ensure students gain a comprehensive understanding of this essential topic. These resources include detailed notes on the principles of elasticity, stress, and strain, as well as the behavior of materials under different forces. Key concepts such as Young’s modulus, bulk modulus, and shear modulus are explained with clarity, along with practical examples to illustrate their real-world applications. Additionally, stress-strain curves are thoroughly analyzed to help students grasp the elastic and plastic behavior of materials. These resources also include problem-solving exercises and diagrams to reinforce understanding and prepare students for exams effectively.
What Are the Mechanical Properties Of Solids?
The concept of “Mechanical Properties of Solids” in Class 11 Physics delves into the foundational principles of science by exploring the methods and standards used to quantify and describe physical phenomena. This chapter introduces students to the behavior of materials under different forces, explaining concepts like elasticity, plasticity, and various types of stress and strain. It covers fundamental laws such as Hooke’s Law and the modulus of elasticity, helping students understand how solids respond to tension, compression, and shear forces. Additionally, the chapter explains the significance of stress-strain curves in determining material strength and applications in construction and engineering. Through these principles, students gain a comprehensive understanding of the mechanical behavior of solids in everyday life and industrial applications.
Elasticity
Elasticity is the property of a body that allows it to regain its original shape and size when an external force is removed. Substances that exhibit this behavior are called elastic substances.
- Examples of Elastic Substances are– catapults, rubber bands, and steel rings.

| Elasticity Example | Action | Behavior |
| Unstretched spring | Force applied | Spring stretches |
| Stretching due to force | Force removed | Spring regains original shape |
Plasticity
Substances that do not regain their original shape and size after the removal of force are called plastic substances, and their behavior is termed plasticity.
- Examples: Mud and putty, which get permanently deformed when an external force is applied.
Elastic Behavior of Solids
In solids, atoms or molecules are held together by intermolecular forces. When a solid is deformed, these particles are displaced from their equilibrium positions. Upon removal of the deforming force, these forces bring the particles back to their original positions, thus restoring the solid’s shape.
This behavior can be illustrated using the ball-spring model. The balls represent atoms, and the springs represent intermolecular forces. When a force is applied to the ball, the spring stretches, and upon removal, the ball returns to its original position.
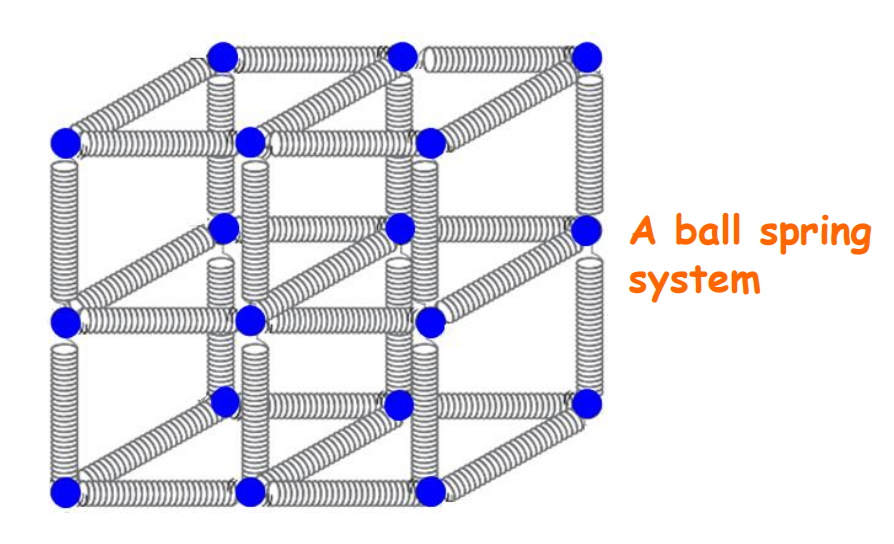
Elasticity Terminology
Deforming Force
A deforming force is any force that changes the shape, size, or volume of an object.
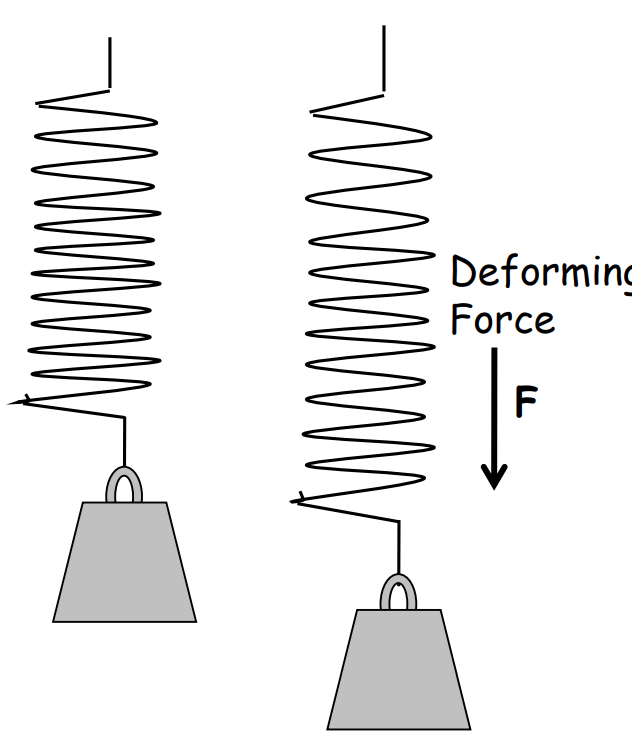
Perfectly Plastic Body
A perfectly plastic body does not regain its original shape or size after the removal of a deforming force. While no real substance is perfectly plastic, paraffin wax is a near-perfect example.
Stress
Stress is defined as the internal restoring force per unit area acting in a direction opposite to the deforming force.
Stress=Restoring Force/Area
The SI unit of stress is N/m² (Pascal), and its dimensional formula is [ML⁻¹T⁻²].
Types of Stress
| Type of Stress | Description |
| Normal Stress | Developed when force is perpendicular to the surface |
| Tensile Stress | Stress that increases length or extension |
| Compressive Stress | Stress that decreases length |
| Hydraulic Stress | Stress causing a change in volume without altering shape |
| Tangential Stress | Stress causing a change in shape, also known as shearing stress |
Tensile Stress Compressive Stress Hydraulic Stress Tangential Stress
Strain
Strain is the ratio of the change in configuration to the original configuration. It has no unit and is dimensionless. Depending on the stress type, strain can be:
- Longitudinal Strain – Change in length. It is also called the tensile strain. Let the length of a cylinder be L and let its length change by L by the action of deforming force, then,
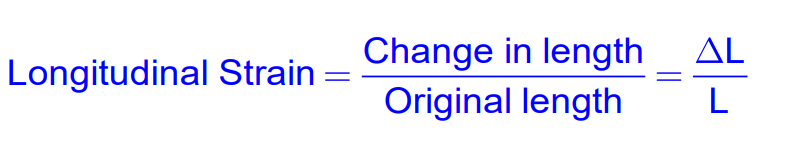
- Volume Strain – Change in volume. It is the ratio of displacement of a surface under a tangential force to the perpendicular distance of the displaced surface from the fixed surface.

- Shearing Strain – Change in shape. Within the limit, the object can retain its property of elasticity and regain its original shape and size completely; when the deforming force is removed, it is called the elastic limit. Beyond a certain limit, a body loses the property of elasticity and gets permanently deformed.
Hooke’s Law
Hooke’s Law states that within the elastic limit, the stress developed in a body is directly proportional to the strain produced. Mathematically:
Stress∝Strain or Stress=kxStrain
Here, k is the modulus of elasticity.
Stress-Strain Curve
The relationship between stress and strain can be plotted on a graph. Initially, the graph is a straight line, confirming Hooke’s law, but beyond a certain point (yield point), stress increases rapidly with strain, leading to permanent deformation.
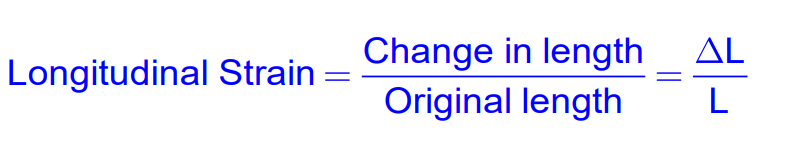
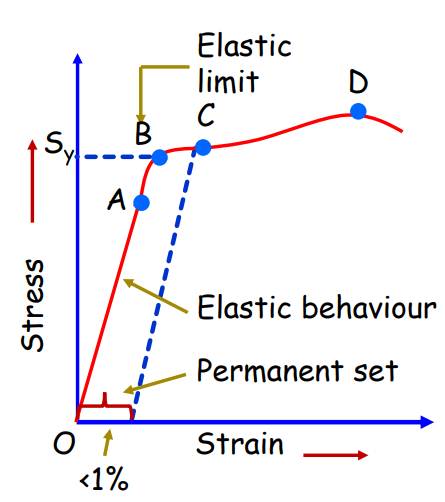
Points on Stress-Strain Curve Description O to A Hooke’s law applies, stress is proportional to strain B Yield point, elastic limit C Ultimate tensile strength E Fracture point, material breaks
Ductile vs Brittle Materials
- Ductile Materials: Points D and E on the stress-strain curve are far apart.
- Brittle Materials: Points D and E are closer together.

Elastomers
Substances like rubber and aorta tissue can be stretched to large strains and are called elastomers. These materials do not obey Hooke’s law.
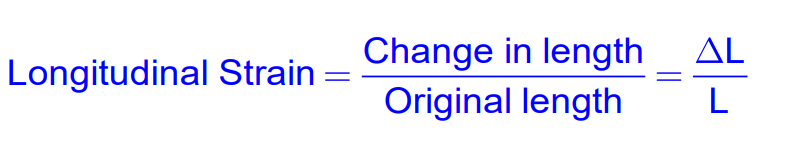
Elastic Moduli
The modulus of elasticity is the ratio of stress to strain and depends on the material and type of deformation. Types of moduli include:
- Young’s Modulus: Ratio of normal stress to longitudinal strain.
- Shear Modulus (Modulus of Rigidity): Ratio of tangential stress to shearing strain.
- Bulk Modulus: Ratio of normal stress to volumetric strain.
Young’s Modulus
- The ratio of normal stress to longitudinal strain is termed as Young’s modulus.
- Young’s modulus is denoted by letter Y.
- Unit of Young’s modulus is N/m2.
- Young’s modulus is found to be a characteristic property of a material.
- Its value is larger for metals.
- It is represented as:

Where:
- F = Force applied
- A = Area
- L = Original length
- ΔL = Change in length
Experimental Set-up for Determining Young’s Modulus Modulus
- A and B are two long, straight wires of nearly equal length, same cross sectional area and A B same material.
- The wires are suspended from a fixed support.
- Wire A, the reference wire, has a pan attached to its free end to place the load.
- A vernier scale is fixed at the bottom of the experimental wire and the main scale is fixed to the reference wire.
- The weights placed in the experimental wire exert a downward force and stretch the wire.
- The increase in length of the wire is measured by the vernier arrangement. Vernier scale The reference wire compensates the change in length due to the factors other than the weight.
- Let r and L be the initial radius and length of the experimental wire and let M be the mass that produced the elongation ΔL in the wire. The Young’s modulus of the material of the wire is given by:
Shear Modulus
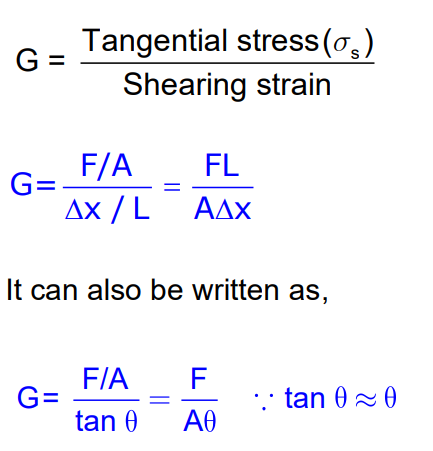
Where:
- F= Tangential force
- A= Area
- Δx = Displacement
- L = Length
Bulk Modulus
B=Normal Stress/Volumetric Strain
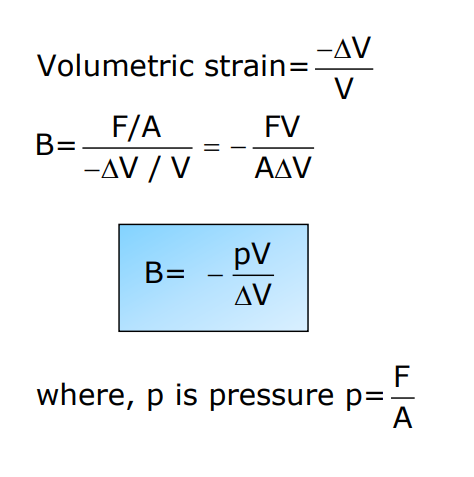
Where p is pressure, and V is volume.
- The unit of bulk modulus is N/m2.
- Negative sign signifies that with increase in pressure, volume decreases.
- The reciprocal of bulk modulus is called compressibility.
- Compressibility is denoted by the letter K. Hence, Compressibility (K)= 1/B
Applications of Elastic Behavior
Elastic behavior is crucial in daily life, especially in construction and material design:
- The elastic limit of materials used in machinery ensures they don’t undergo permanent deformation.
- The thickness of ropes in cranes is determined based on the material’s elasticity.
Beam Design
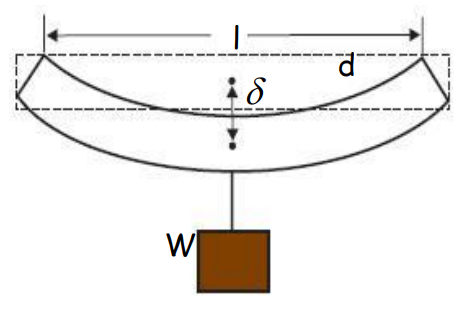
In construction, beams are designed to avoid bending and buckling. To reduce bending, materials with high Young’s modulus are chosen, and increasing the depth of a beam is more effective than increasing its breadth. The I-shaped beam is commonly used to prevent buckling while minimizing weight.
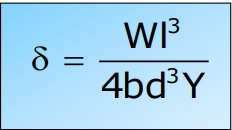
Pillar Design
Pillars with distributed ends support more load than those with rounded ends, making them more effective in construction.
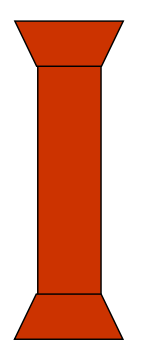
Conclusion
This comprehensive guide on “Mechanical Properties of Solids” provides an in-depth exploration of the fundamental aspects of physics as outlined in Class 11. It covers the core concepts of elasticity, plasticity, and stress-strain relationships, offering insights into how materials behave under various forces. The guide explains the importance of standardization in measurements, ensuring accurate and consistent analysis of mechanical properties. It delves into key principles such as Hooke’s Law, elastic moduli (Young’s modulus, bulk modulus, and shear modulus), and the significance of stress-strain curves in understanding material strength. Additionally, the guide emphasizes practical applications, including beam and pillar design, and the role of elasticity in real-world engineering and construction, making it a crucial resource for students and professionals alike.
Practice questions on Chapter 9 - Mechanical Properties of Solids
Get your free Chapter 9 - Mechanical Properties of Solids practice quiz of 20+ questions & detailed solutions
Practice Now








