System of Particles and Rotational Motion – Complete Guide For Class 11 Physics Chapter 7
Welcome to iPrep, your Learning Super App. Our learning resources for Chapter 7, “System of Particles and Rotational Motion,” in Class 11 Physics are meticulously designed to ensure students gain a comprehensive understanding of this essential topic. These resources include detailed notes on key concepts such as the center of mass, moments of inertia, and angular momentum, supported by illustrative diagrams and real-world examples. Additionally, the materials feature a range of practice problems and solutions to reinforce theoretical knowledge and enhance problem-solving skills. Interactive simulations and video tutorials are also provided to visually demonstrate complex concepts and facilitate a better grasp of the subject matter. Overall, these resources aim to build a solid foundation in rotational dynamics and its applications in various physical systems.
What is the System of Particles and Rotational Motion?
The concept of “System of Particles and Rotational Motion” in Class 11 Physics delves into the foundational principles of science by exploring the methods and standards used to quantify and describe physical phenomena. This chapter introduces students to the fundamental principles of mechanics, including the concepts of force, torque, and angular velocity. It examines how these principles apply to systems of particles and rotating bodies, emphasizing the role of inertia and the effects of external forces on rotational motion. Students learn about the conservation of angular momentum and how it governs the behavior of rotating systems. Through practical examples and problem-solving exercises, this chapter helps students understand the intricacies of rotational dynamics and its relevance to real-world applications.
Rigid Body
- A rigid body has a definite shape and size.
- The distance between any two particles of a rigid body remains the same even when external forces are applied.
- Practically, nobody is perfectly rigid.
An extended body can be considered a system of particles. In a system of N particles, they can change their positions relative to one another. However, in a rigid body, the particles remain at their respective positions. Thus, the term system of particles includes rigid bodies as a special case.
Types of Motion in a Rigid Body
A rigid body can exhibit the following kinds of motion:
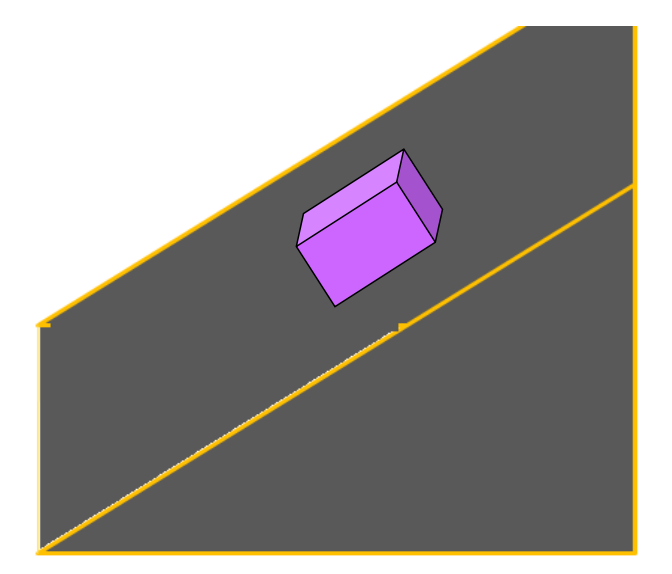
- Pure Translational Motion: Example – A block sliding down an inclined plane.
- Pure Rotational Motion: Example – The blades of a ceiling fan.
- Combination of Translational and Rotational Motion: Example – The motion of tires on a moving vehicle.

Pure Translational Motion
In this motion, all particles of a body move together with the same velocity. Example: A rectangular block sliding down an inclined plane.
Pure Rotational Motion
In pure rotational motion, a rigid body rotates about a fixed axis. Every particle (except those on the axis of rotation) moves in a circle, which lies in a plane perpendicular to the axis. The center of the circle is on the axis.
Examples:
- The motion of a ceiling fan.
- A potter’s wheel.
- A giant wheel in a circus.
Illustration of Pure Rotational Motion
The particles of a rigid body describe different radii around the axis of rotation. The following diagram illustrates this:
Particle Radius from axis Description P1 r1 Lies in a plane perpendicular to the axis, with its center on the axis P2 r2 Same as P1, but with a larger radius P3 r = 0 Lies on the axis and does not describe a circle 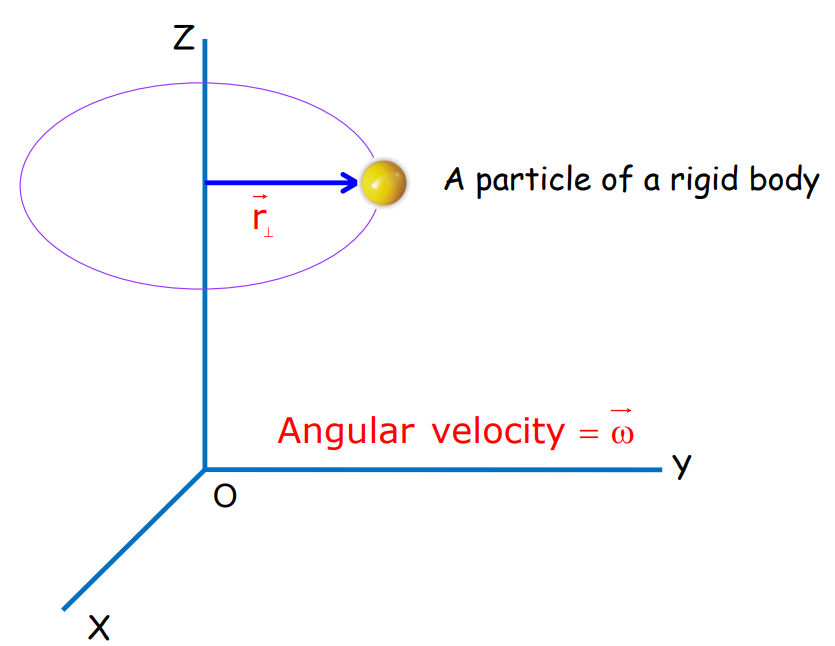
Combination of Translational and Rotational Motion
In this type of motion, a body exhibits both translational and rotational motions. The axis of rotation is not fixed. Example: A rolling wheel.

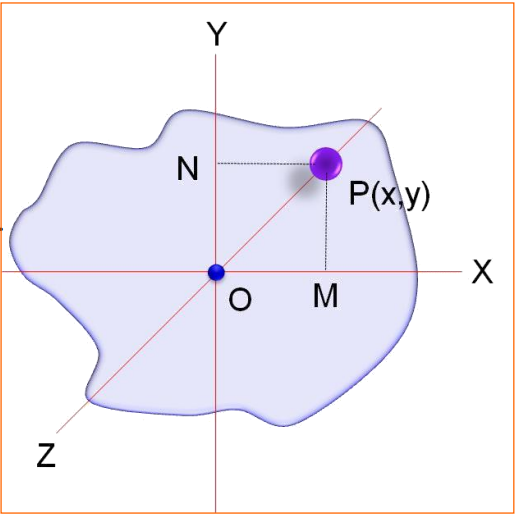
Center of Mass (C.M.)
The center of mass is an imaginary point where the entire mass of the system or object is considered to be concentrated. The total mass of a system doesn’t need to be actually present at the center of mass.
C.M. of a Two-Particle System
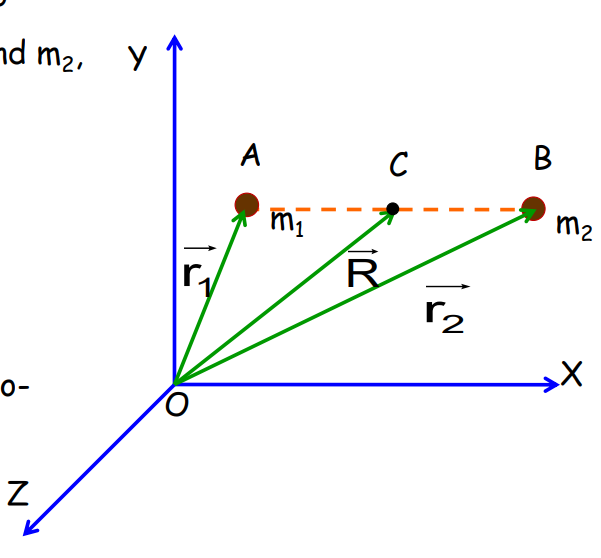
Consider two particles of masses m1m_1m1 and m2m_2m2 at distances r1r_1r1 and r2r_2r2 from the origin. The position vector of the center of mass is given by:
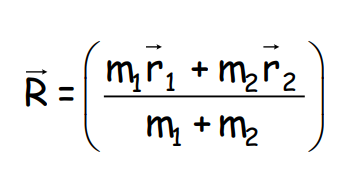
The forces acting on the system are:
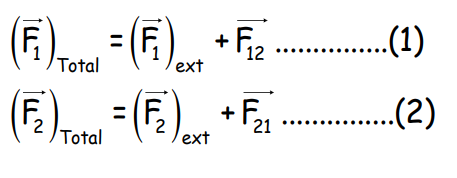
Equation of Motion for a Two-Particle System
The equation of motion for masses m1 and m2 are:
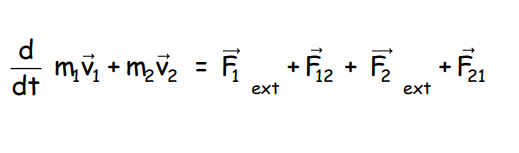
Center of Mass of a Rigid Body

A rigid body can be considered a system of closely packed particles. The space between these particles is so small that the body can be treated as a continuous distribution of mass.
The center of mass of a rigid body is found by summing over infinitesimal mass elements:
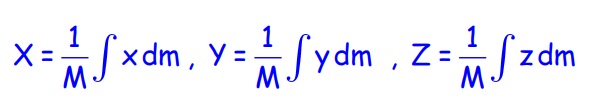
Center of Mass of a Uniform Rod
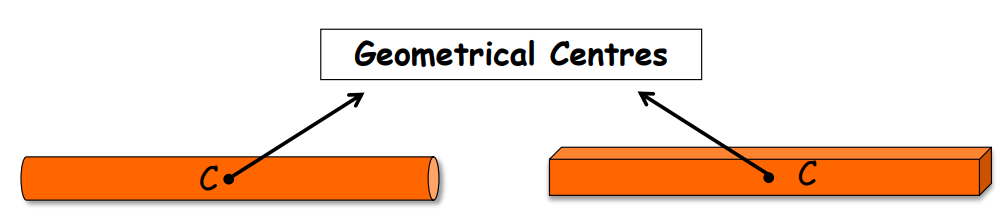
For a uniform rod, the center of mass coincides with the geometric center of the rod. Since the rod is symmetrical about its center, for every mass element at distance +x, there is an equivalent element at distance −x, making the center of mass:
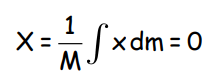
Center of Mass of Objects with Regular Shapes
| Object | Position of C.M. |
| Uniform hollow sphere | Center of the sphere |
| Uniform solid sphere | Center of the sphere |
| Uniform circular ring | Center of the ring |
| Uniform circular disc | Center of the disc |
| Uniform rod | Center of the rod |
| Planar body (lamina) | Point of intersection of diagonals |
Motion of the Center of Mass
The motion of the center of mass for a system of ‘n’ particles is given by:
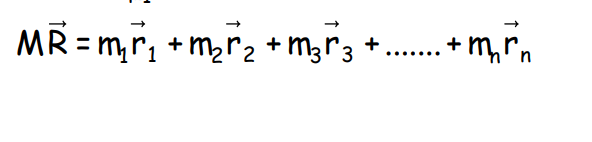
Differentiating with respect to time gives:
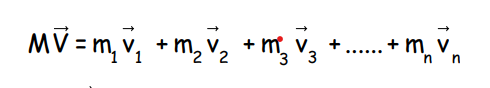
Thus, the velocity of the center of mass depends on the velocities of all particles in the system.
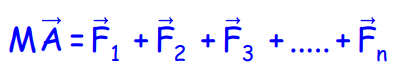
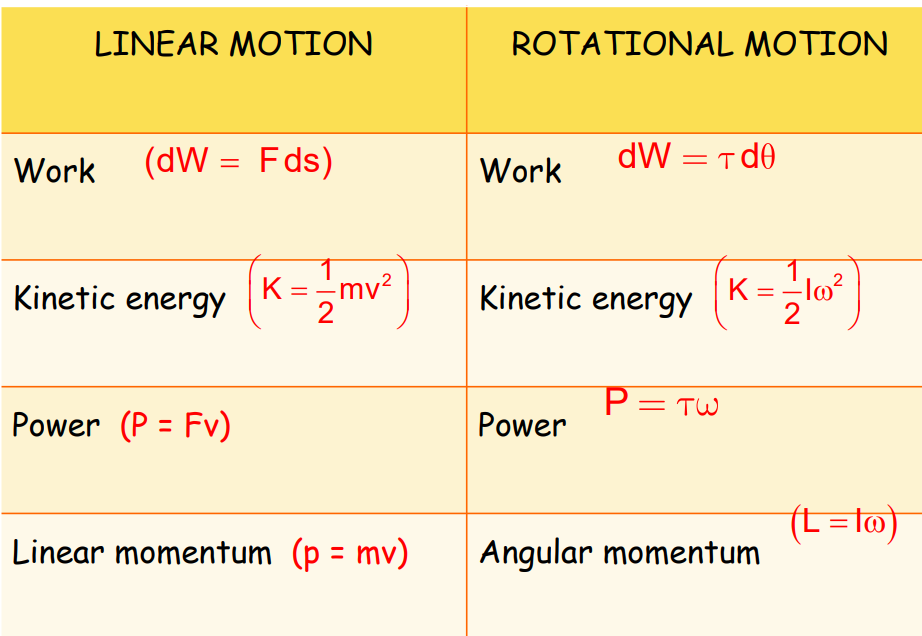
Linear Momentum of a System of Particles
The linear momentum of a system of particles is the vector sum of the individual momenta. If no external forces are acting on the system, the linear momentum remains constant:
P=∑mivi
Principle of Conservation of Linear Momentum
In an isolated system, if the sum of external forces is zero, the linear momentum remains constant. Mathematically:
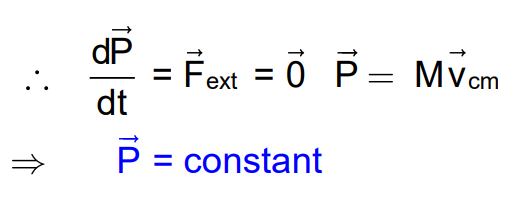
Vector Product of Two Vectors
The vector (or cross) product of two vectors a and b is defined as:
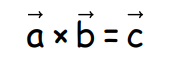
The magnitude of the vector product is
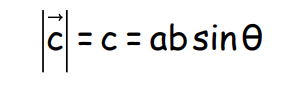
where, θ is the angle between vectors a and b.
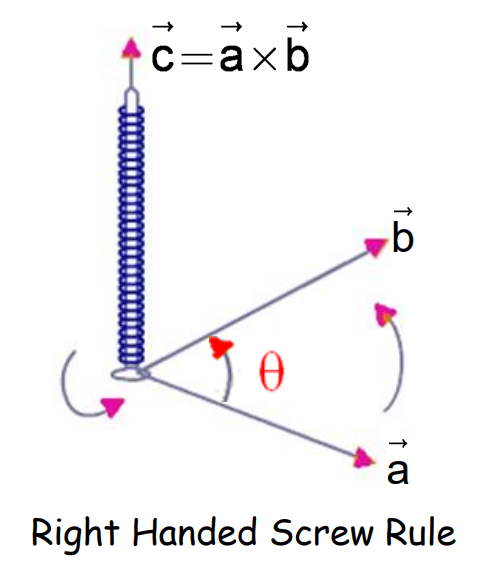
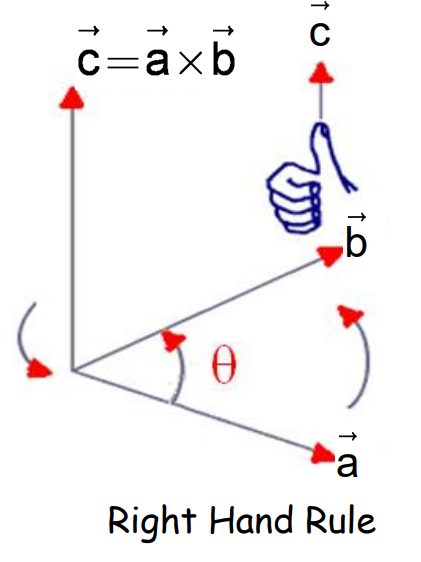
The direction of c is perpendicular to the plane containing vectors a and b.
Properties of Vector Products
- Not Commutative: Cross product or vector product is not commutative.Vector product is distributive.
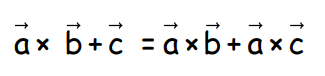
- Distributive: Vector product of two vectors is associative.
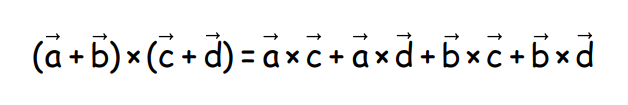
- Cross Product of a Vector with Itself: Cross product of a vector with itself is zero.
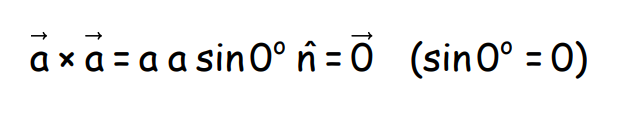
- Vector product of the reflections of two vectors is equal to that of the original vectors.

Vector Products of Unit Vectors
The cross product of unit vectors is as follows:
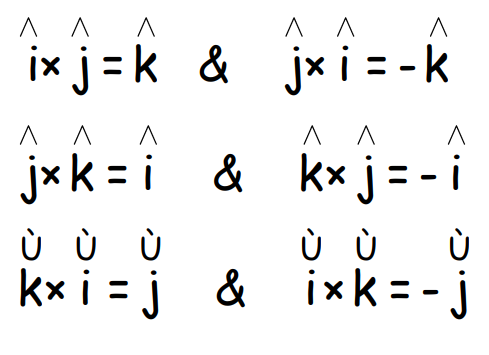
Expression for a×b
In three dimensions, the vector product of two vectors for a and b in determinant form is:
Angular Velocity
Consider a particle moving in a circle with center O. At time t1, the particle is at P1 with angular position θ1, and at time t2, the particle is at P2 with angular position θ2.
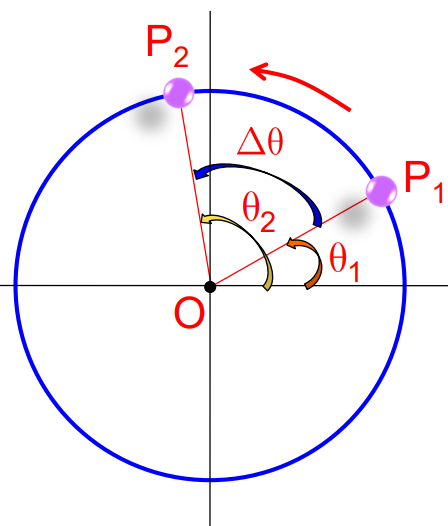
Average Angular Velocity

Instantaneous Angular Velocity
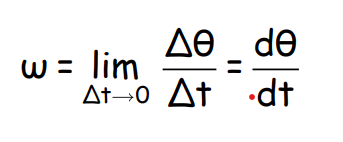
If the particle rotates through equal angles in equal time intervals, it is said to have uniform angular velocity.
Relation Between Angular and Linear Velocity
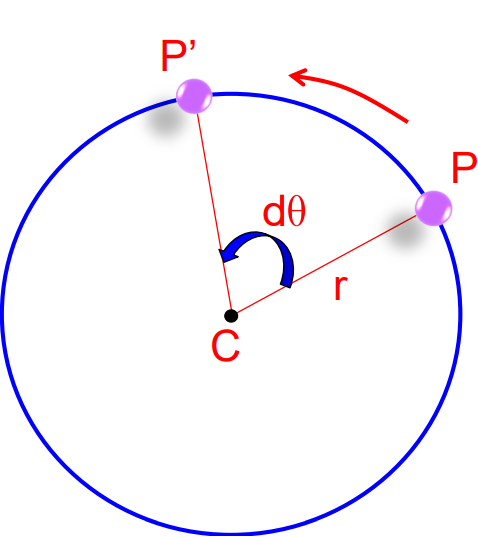
Consider a particle moving in a circle of radius r:
v=rω
In vector notation:

Particles located farther from the axis of rotation have higher linear velocities.
For Particles on the Axis of Rotation
For a particle on the axis of rotation, r=0, so the linear velocity is zero. Hence, particles on the axis have no translational motion.
v=rω=0
Angular Acceleration
Angular acceleration α is the rate of change of angular velocity.
Average Angular Acceleration
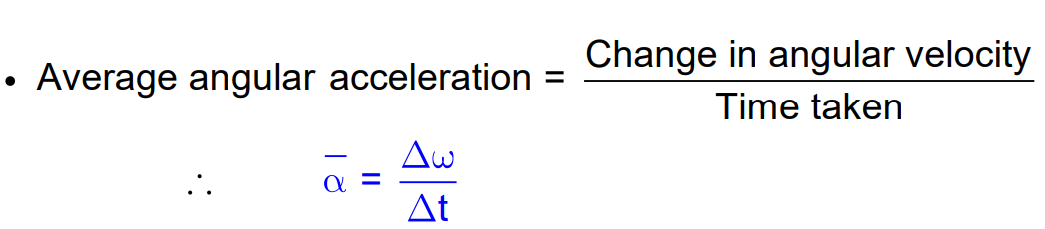
Instantaneous Angular Acceleration
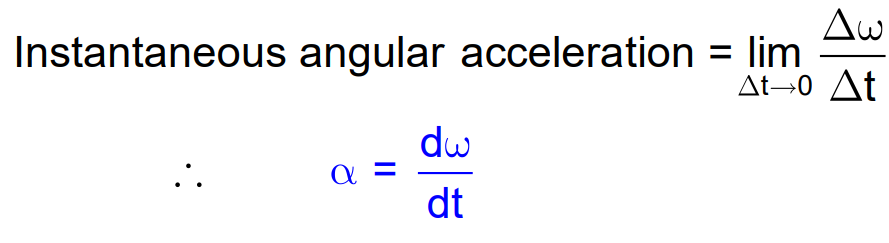
Relation Between Angular and Linear Acceleration
The relation between linear and angular velocity is v=rω. Differentiating this equation with respect to time:
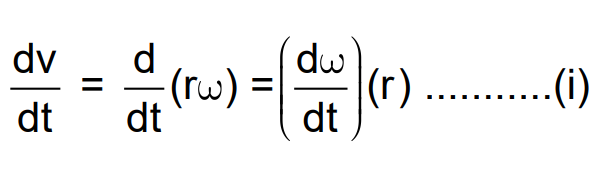
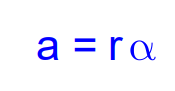
This implies that linear acceleration is the product of angular acceleration and radius.
Torque or Moment of Force

Torque is defined as the turning effect of a force about a fixed point or axis. Mathematically, torque τ is:
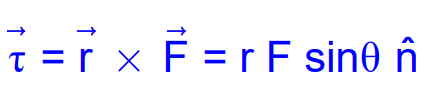
Where n^ is the unit vector perpendicular to both r and F. Its SI unit is N-m, and its dimensional formula is [ML2T−2].
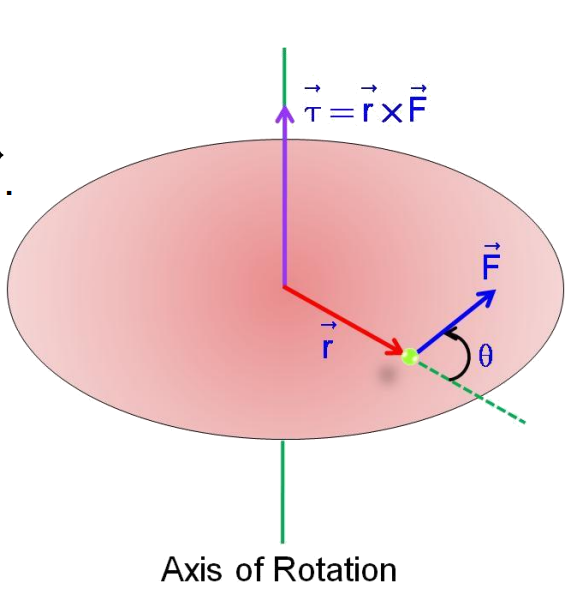
Special Cases: Axis of Rotation
- If θ=0∘, τ=0.
- If θ=90∘, τ=rF(maximum).
Angular Momentum of a Particle
Angular momentum lll is the product of linear momentum and the perpendicular distance of the momentum vector’s line of action from the axis of rotation.
l=r×p
In determinant form:
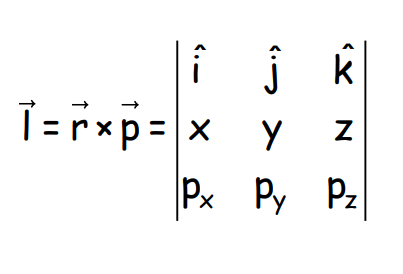
Relation Between Angular Momentum and Torque
The rate of change of angular momentum is equal to the torque acting on it:
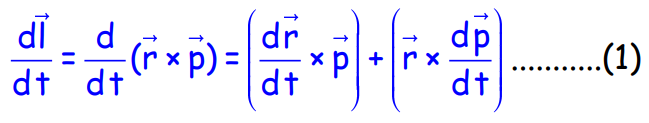
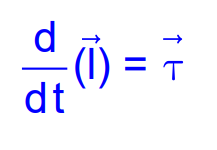
This is the rotational equivalent of Newton’s Second Law.
Angular Momentum and Torque for a System of Particles
The total angular momentum of a system of n particles is:
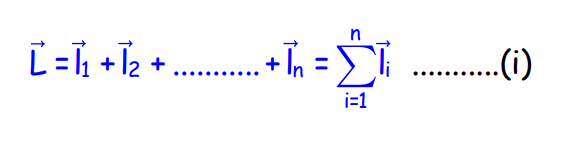
The total external torque is related to the rate of change of total angular momentum:
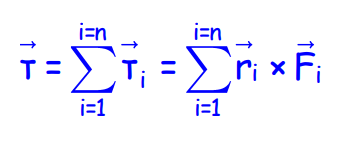
Law of Conservation of Angular Momentum
When no external torque acts on a system, the total angular momentum remains constant:
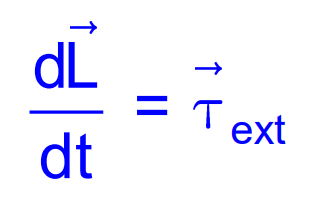

Equilibrium of a Rigid Body
A rigid body is in mechanical equilibrium if both its linear and angular momentum do not change with time.
First Condition of Equilibrium
The net external force acting on the body must be zero:
∑F=0
This ensures translational equilibrium.
Second Condition of Equilibrium
The net external torque acting on the body must be zero:
∑τ=0
This ensures rotational equilibrium.
Principle of Moments
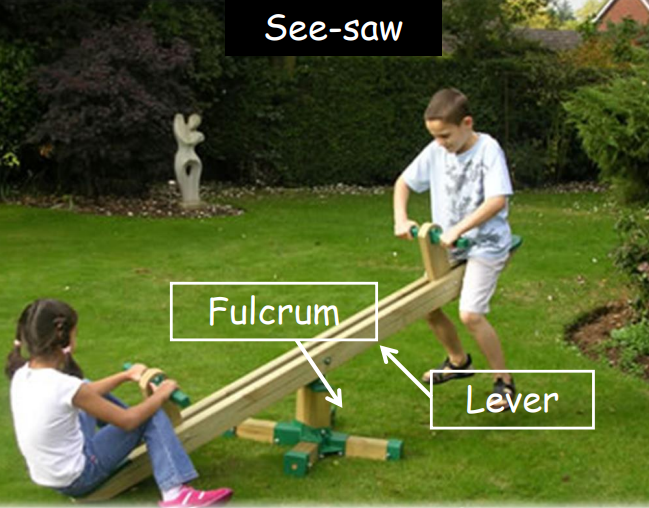
A body is in rotational equilibrium if the sum of anticlockwise moments equals the sum of clockwise moments.
In simple terms, for a lever:
F1d1=F2d2
Where F1 and F2 are the forces, and d1 and d2 are the respective distances from the fulcrum.
Mechanical Advantage
The mechanical advantage (M.A.) of a lever is:
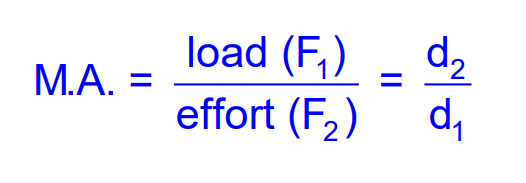
If M.A. > 1, a small effort is required to lift a heavy load.
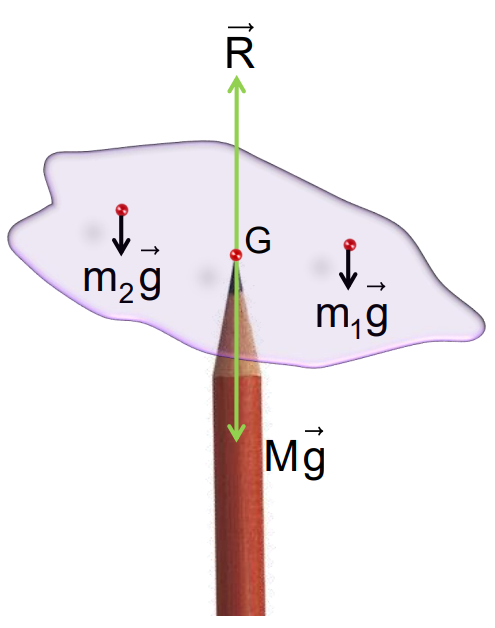
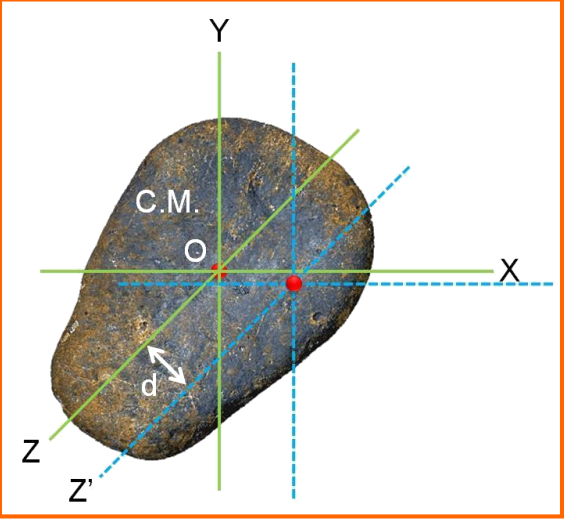
Centre of Gravity
The center of gravity (C.G.) of a body is the point where the total gravitational torque on the body is zero. It coincides with the center of mass in uniform gravity.
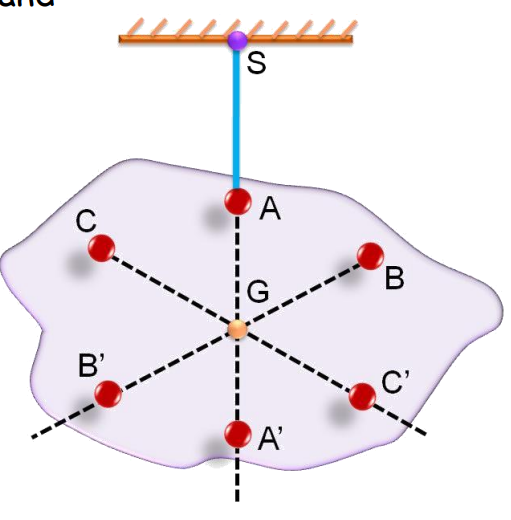
Determination of Centre of Gravity
To find the center of gravity of an irregular body, suspend the body from different points and mark the vertical lines. The intersection of these lines gives the center of gravity.
Kinetic Energy of Rotation
The rotational kinetic energy of a body is:
K.E.=1/2Iω2
Where III is the moment of inertia, and ω\omegaω is the angular velocity.
Moment of Inertia
The moment of inertia III is the sum of the products of the masses of all particles and the square of their perpendicular distances from the axis of rotation:
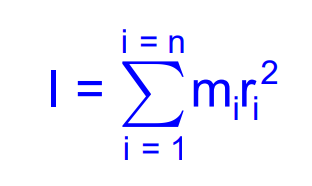
It plays the same role in rotational motion as mass does in linear motion.
Applications of Moment of Inertia
Flywheels, propellers, and rotors make use of moment of inertia to regulate motion, store energy, or provide stability.

M.i.’s of Some Regular Shaped Bodies
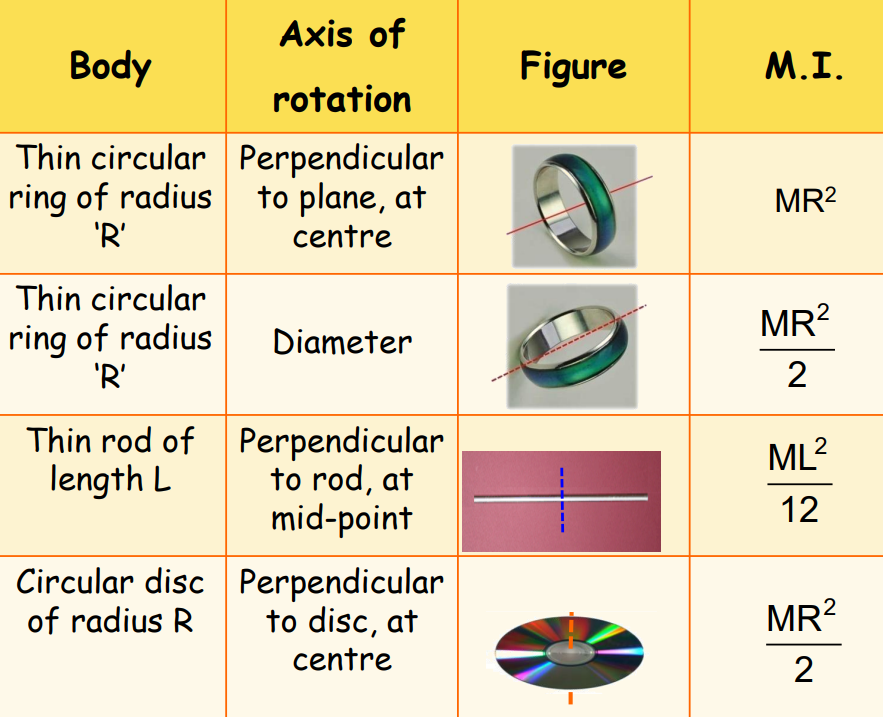
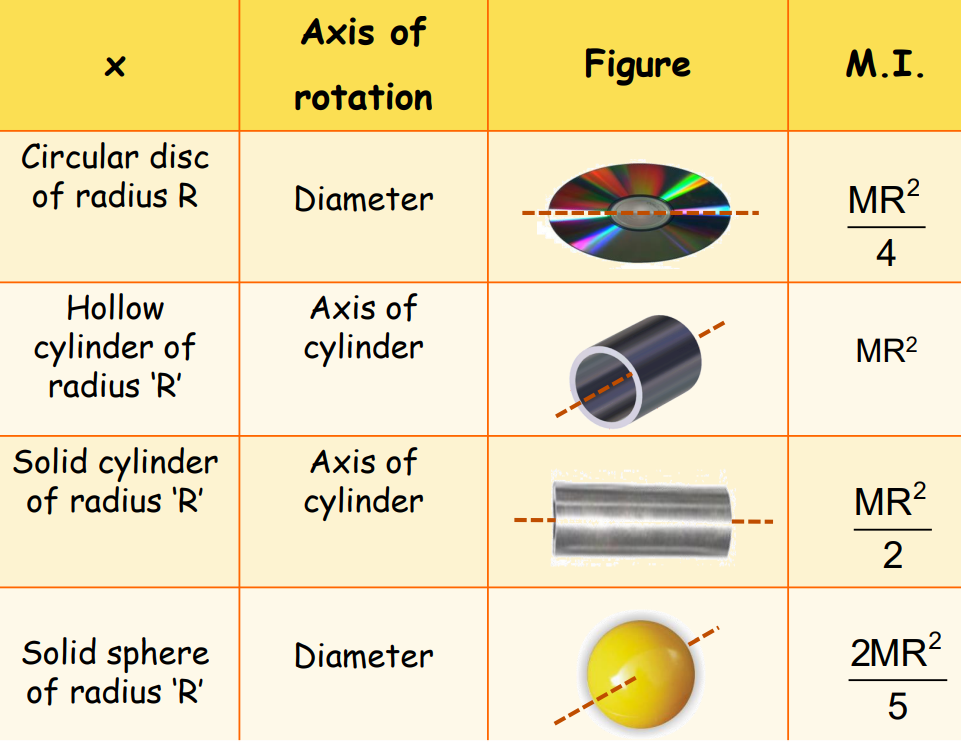
Radius of Gyration
The radius of gyration kkk is the perpendicular distance from the axis of rotation at which, if the entire mass of the body were concentrated, the moment of inertia would be the same as that with the actual distribution of mass. It is a measure of how the mass is distributed relative to the axis of rotation.
Units and Dimensional Formula
- SI Unit: meters (m)
- Dimensional Formula: [M^0L^1T^0]
Relation with Moment of Inertia
The radius of gyration kkk is related to the moment of inertia III by the equation:
I=Mk^2
where M is the mass of the body.
Radius of Gyration of a Thin Rod
Rod Rotating About an Axis Through Its Center
For a thin rod of mass M and length L rotating about an axis perpendicular to its length and passing through its center, the moment of inertia III is given by:
I=ML^2/12
Using the definition of radius of gyration:
I=Mk^2, Equating the two expressions for III:
Solving for k:
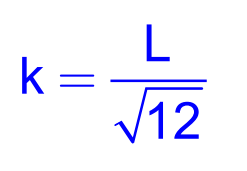
This implies that the rod has the same moment of inertia as a particle of mass M located at a distance from the axis.
Distance =
Perpendicular Axis Theorem
The moment of inertia of a planar object about an axis perpendicular to its plane is the sum of its moments of inertia about two perpendicular axes in the plane:
Iz=Ix+Iy
This theorem is useful for analyzing moments of inertia for flat objects like discs, rings, and rods.
Parallel Axis Theorem
If the moment of inertia of a body about an axis passing through its center of mass is IcmI_{\text{cm}}Icm, then the moment of inertia about a parallel axis at a distance d from the center of mass is:
I=MR^2
Where M is the mass of the body.
Kinematics of Rotational Motion About a Fixed Axis
The kinematic equations for rotational motion of a body with constant angular acceleration α are:
Comparison of Rotational and Translational Kinematics
Dynamics of Rotational Motion About a Fixed Axis
A force applied to a rotating body performs work, which can be expressed in terms of torque and angular displacement. Key considerations include:
- Forces must be in planes perpendicular to the axis of rotation.
- Only components of position vectors perpendicular to the axis are considered.
Work Done by a Force
- Work done by Force F1 on a particle:
Torque and Work Done
- Torque due to Force F1F_1F1: τ=r1F1sinθ
- Total Work Done by Several Forces: dW=τ⋅dθ
- This is analogous to dW=Fds
Power of the Rotating Body
Differentiating the work done equation with respect to time:
dWdt=τ⋅dθ
Where dθdt is the angular velocity ω, giving:
P=τ⋅ωP = P=τ⋅ω
Kinetic Energy of Rotational Motion
The kinetic energy of a rotating body is given by:
K=1/2Iω^2
Differentiating with respect to time:
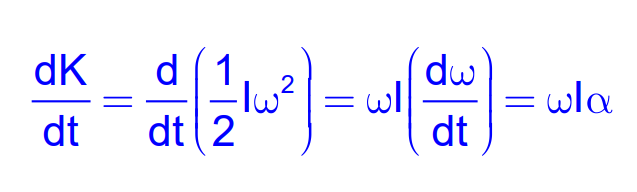
This shows that torque produces angular acceleration in a body, analogous to Newton’s second law for rotation.
Comparison of Translational and Rotational Motions

Angular Momentum in Case of Rotation About a Fixed Axis
The angular momentum of a particle in a rigid body can be expressed as:
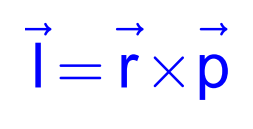
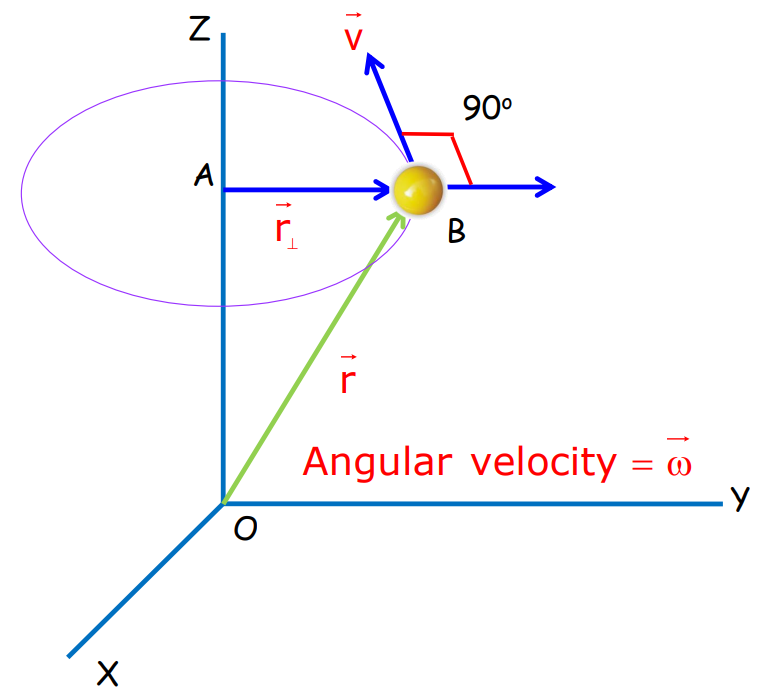
Angular Momentum Components
- For a point with position vector r⃗\vec{r}r and linear momentum p⃗\vec{p}p: L=r⃗×p⃗L = \vec{r} \times \vec{p}L=r×p
Total Angular Momentum
Total angular momentum is the vector sum of the angular momenta of all particles:
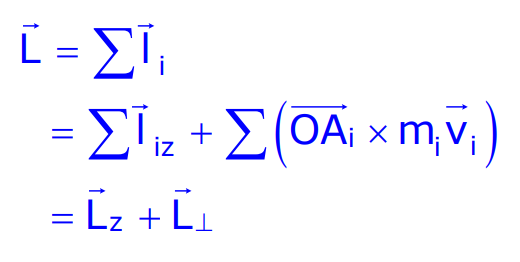
For a symmetric body, the components perpendicular to the total angular momentum are zero, and:
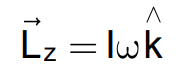
Conservation of Angular Momentum
In the absence of external torques:
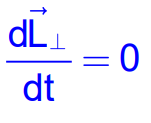
Thus, angular momentum remains constant if no net external torque acts on the system.
Example of Conservation of Angular Momentum
A man on a rotating chair with dumbbells will spin faster when he pulls his arms in, due to the conservation of angular momentum. As his moment of inertia decreases, his angular velocity increases to maintain constant angular momentum.

Rolling Motion
Rolling motion is a combination of translational and rotational motion, where:
- The object’s center of mass moves with velocity vcm.
- The object rotates about its center of mass with angular velocity ω.
Rolling Motion Details
For a disc rolling without slipping:
- The point of contact with the surface is momentarily at rest.
- The condition for rolling without slipping is: vcm=Rω.
Kinetic Energy of Rolling Motion
The total kinetic energy of rolling is:
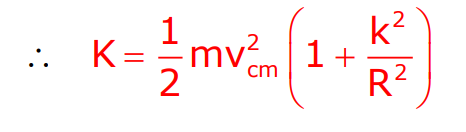
Energy Conservation During Rolling
For a body rolling down an incline from height h:
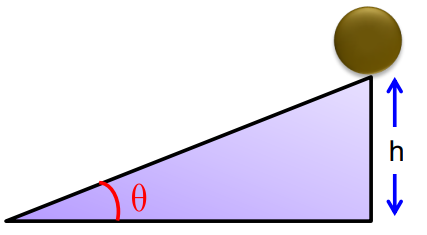
Solving for vcm
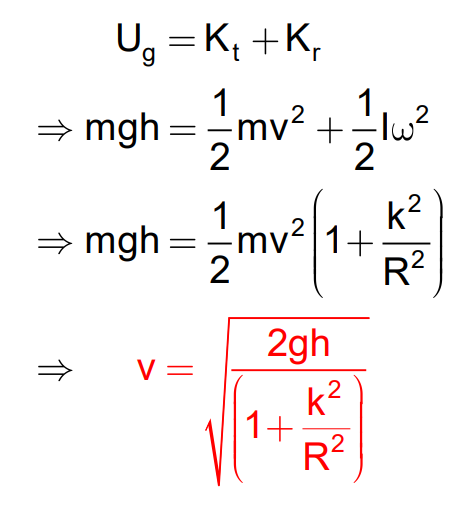
Where k is the radius of gyration and R is the radius of the disc.
Conclusion
This comprehensive guide on “System of Particles and Rotational Motion” provides an in-depth exploration of the fundamental aspects of physics as outlined in Class 11. It covers core concepts of the motion of rigid bodies, torque, and angular momentum. The chapter delves into key principles like the center of mass, moment of inertia, and the relationship between linear and angular quantities. Through mathematical derivations and real-life examples, students learn how rotational motion differs from translational motion and how forces affect systems of particles. This knowledge is crucial for understanding more advanced topics in mechanics and engineering.
Practice questions on Chapter 7 - System of Particles and Rotational Motion
Get your free Chapter 7 - System of Particles and Rotational Motion practice quiz of 20+ questions & detailed solutions
Practice Now








