Motion In A Plane – Complete Guide For Class 11 Physics Chapter 3

Welcome to iPrep, your Learning Super App. Our learning resources for Chapter 3, “Motion in a Plane,” in Class 11 Physics are meticulously designed to ensure students gain a comprehensive understanding of this essential topic. These resources include detailed notes on fundamental concepts such as vector addition and subtraction, resolving vectors into components, and the analysis of motion in two dimensions. Key concepts like projectile motion, relative velocity in two dimensions, and uniform circular motion are explained with clarity. Additionally, the resources provide solved examples, diagrams, and practice problems to reinforce learning and improve problem-solving skills.

The concept of “Motion in a Plane” in Class 11 Physics delves into the foundational principles of science by exploring the methods and standards used to quantify and describe physical phenomena. This chapter introduces students to the study of vectors, which are essential for analyzing quantities with both magnitude and direction. It covers the resolution of vectors into components and their application in two-dimensional motion. Students learn about different types of motion, including projectile motion and uniform circular motion, and the role of acceleration and velocity in such movements. Additionally, the chapter highlights the use of equations of motion in a plane, helping students solve complex real-world problems.

Plane 

A plane is a two-dimensional space. Any point in a plane can be specified by two coordinates, say the x and y coordinates. Any motion in a plane can be described using two coordinate axes.

Scalars

• Scalars are physical quantities that have only magnitude and no direction.
• Examples: Temperature, volume, mass, etc.

Vectors

• Vectors are physical quantities that have both magnitude and direction.
• A vector is represented by a line with an arrowhead.
• Examples: Force, momentum, acceleration, etc. 

Importance of Vectors

• Laws of physics can be expressed in a compact form using vectors.
• Derivations of physical laws can be simplified with vector notation.
• Laws of physics, when expressed in vector form, remain invariant under translation and rotation of the coordinate system.

Definitions in Vector Algebra

Modulus of a Vector

The magnitude of a vector is called its modulus and is represented as |A| or A.

Unit Vector

A unit vector associated with vector A has a magnitude of one and acts along the vector A.

The unit vector n is defined as:

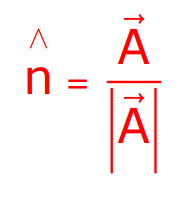
The unit vectors along the X-, Y-, and Z-axes are represented by i, j, and k, respectively. 

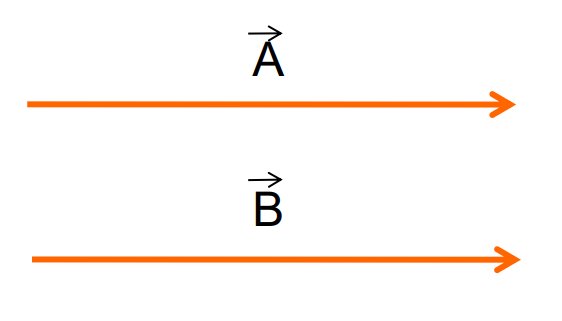
Equal Vectors

Two vectors are said to be equal if they have:

• Equal magnitude
• The same direction

Negative Vector

A negative vector has the same magnitude but acts in the opposite direction to a given vector. If A is the vector, the negative vector is represented as -A.

Co-initial Vectors

Two or more vectors that share a common initial point are called co-initial vectors.

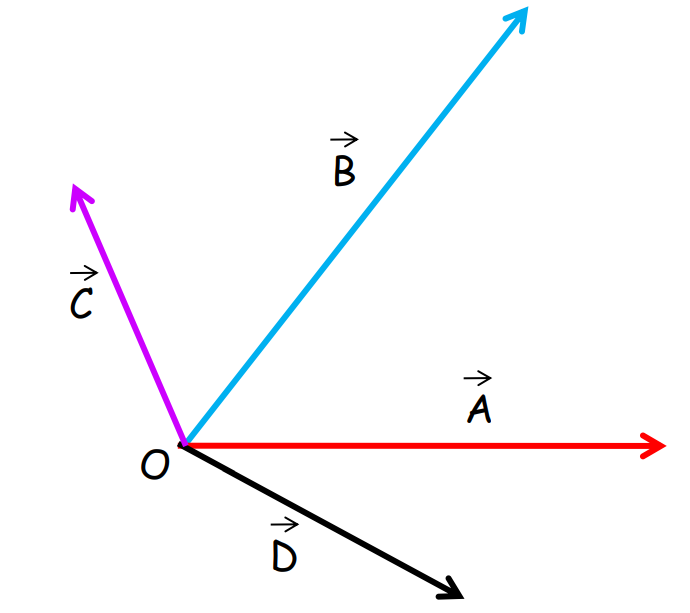
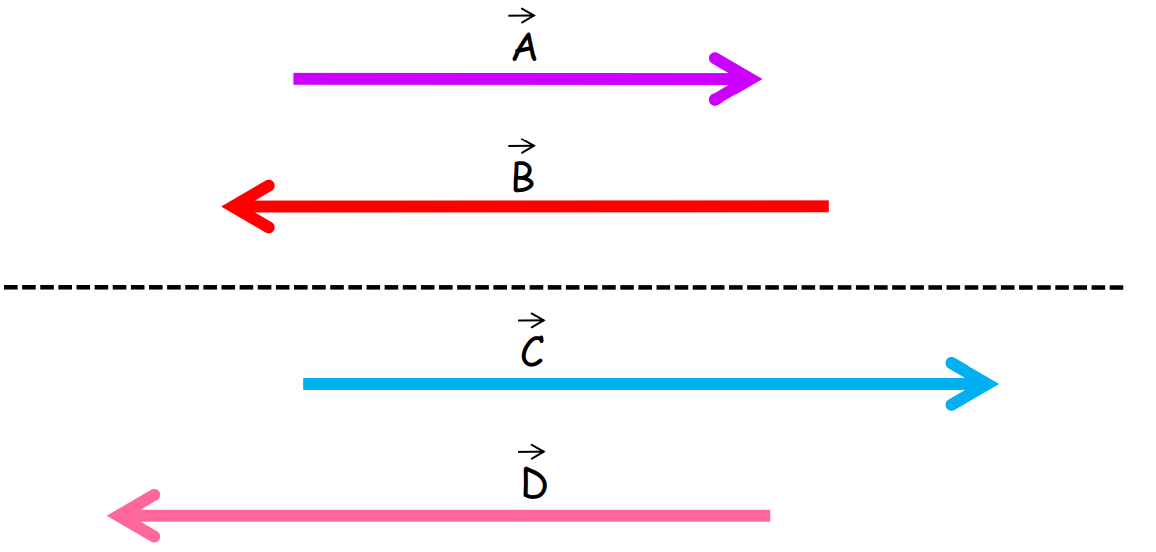
Co-linear Vectors

Vectors that are parallel to a reference line, regardless of their magnitude, are called collinear vectors. 

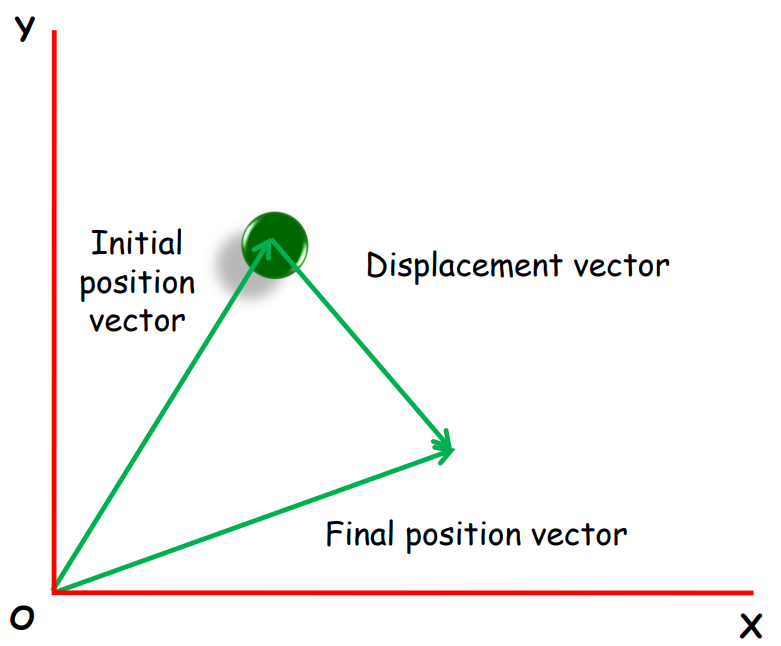
Position Vector in a Plane

A position vector signifies:

• The straight-line distance of an object from its origin.
• The direction of the object’s position concerning the origin.

If O is the origin and P is the position of the object, the position vector is represented as OP. 

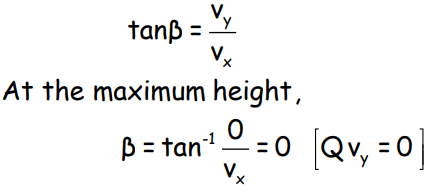
Displacement Vector in a Plane

A displacement vector represents the change in an object’s position in a given time interval. It tells how much and in which direction the object has moved.

• The magnitude of the displacement vector is either less than or equal to the actual path length taken by the object. 

Position Vector and Displacement Vector

Here’s a diagram representing the position vector and the displacement vector:

Multiplication of a Vector by a Real Number

When a vector is multiplied by a real number ‘c’, the resulting vector cA has:

• A magnitude that is ‘c’ times the magnitude of the original vector.

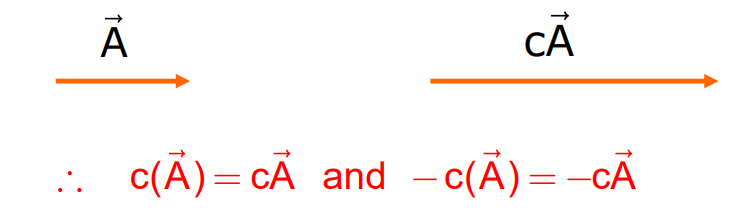
• The same direction as A if ‘c’ is positive, and the opposite direction if ‘c’ is negative.

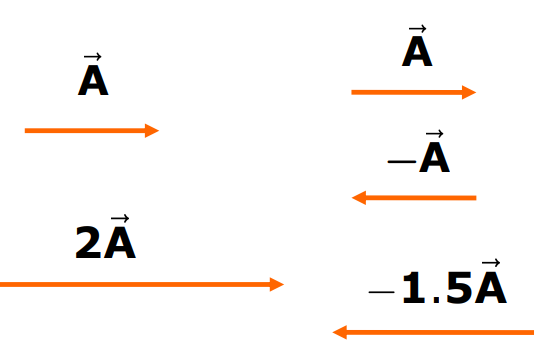
Addition of Vectors

Addition of Vectors by Graphical Method

1. When Two Vectors Are in the Same Direction:
   The magnitude of the resultant vector is the sum of the magnitudes of the individual vectors.

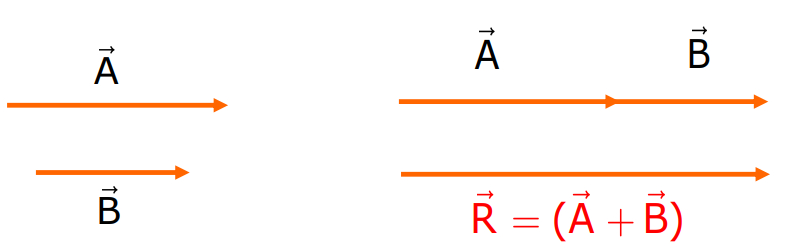
2. When Two Vectors Are in Opposite Directions:
   The magnitude of the resultant vector is the difference between the magnitudes of the two vectors. The direction of the resultant is in the direction of the larger vector.

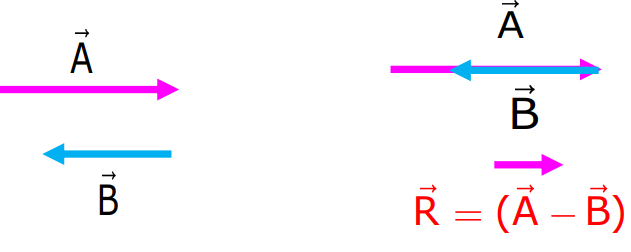
Triangle Law of Vector Addition

The Triangle Law states that if two vectors act on a particle simultaneously, they can be represented by two sides of a triangle taken in order. The resultant vector is represented by the third side of the triangle, taken in the opposite order.

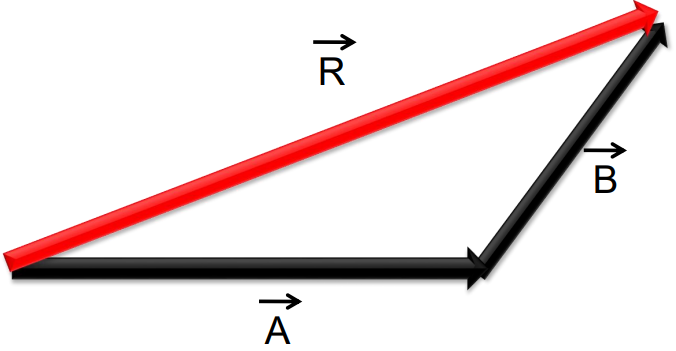
For two vectors A and B:

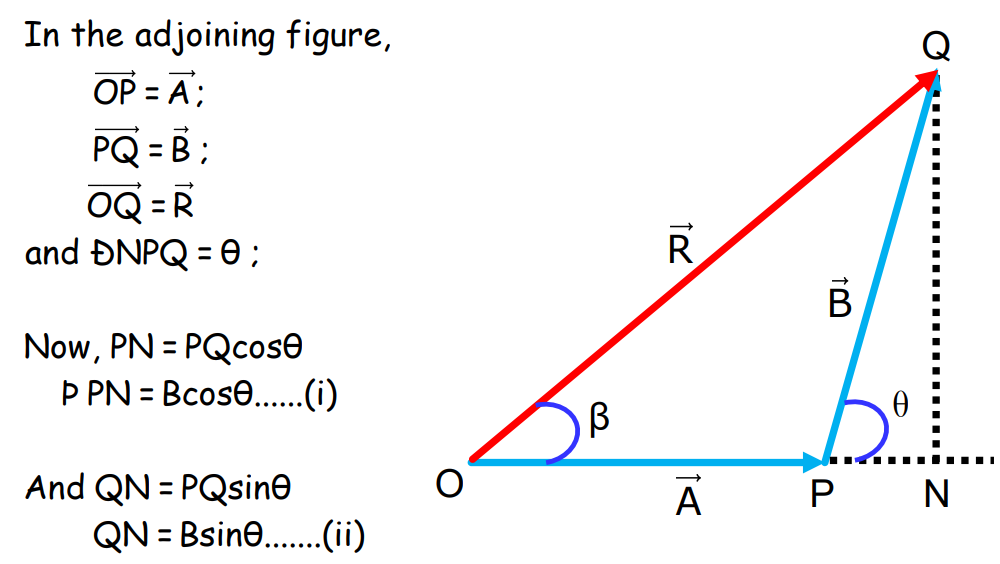
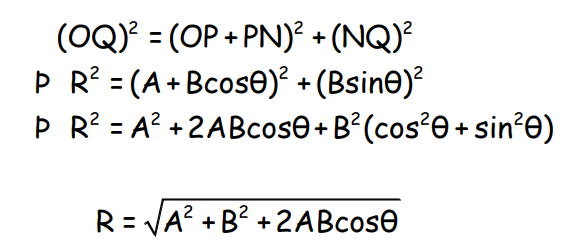
Where:

• A is the magnitude of the first vector,
• B is the magnitude of the second vector,
• θ is the angle between the two vectors. 

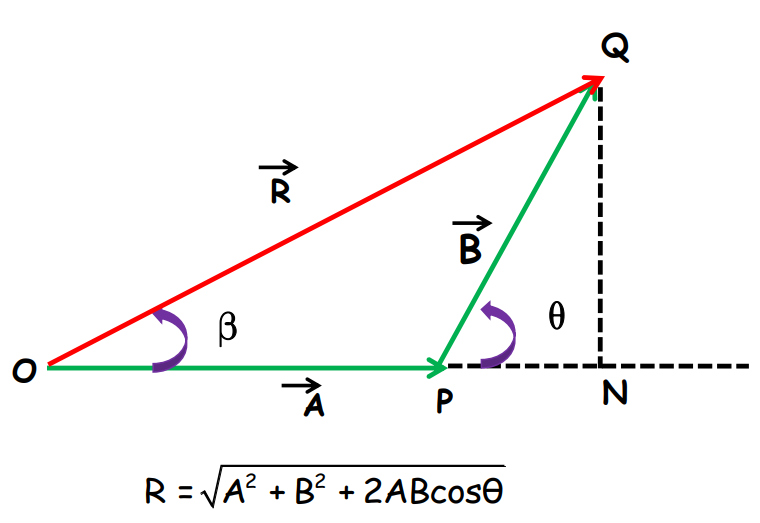
Parallelogram Law of Vector Addition

The Parallelogram Law states that if two vectors are represented by the adjacent sides of a parallelogram, their resultant is represented by the diagonal of the parallelogram drawn from the same point.

For vectors A and B, the magnitude of the resultant vector R is given by:

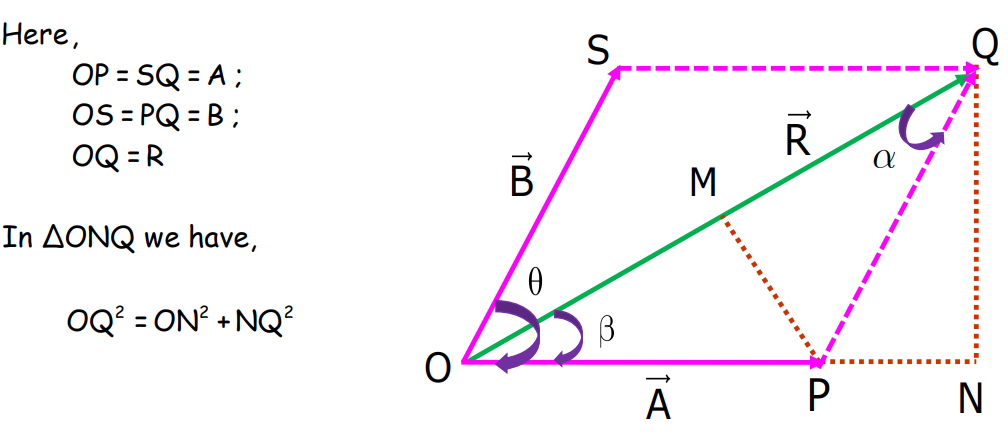
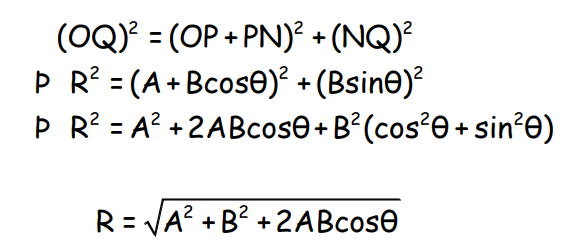
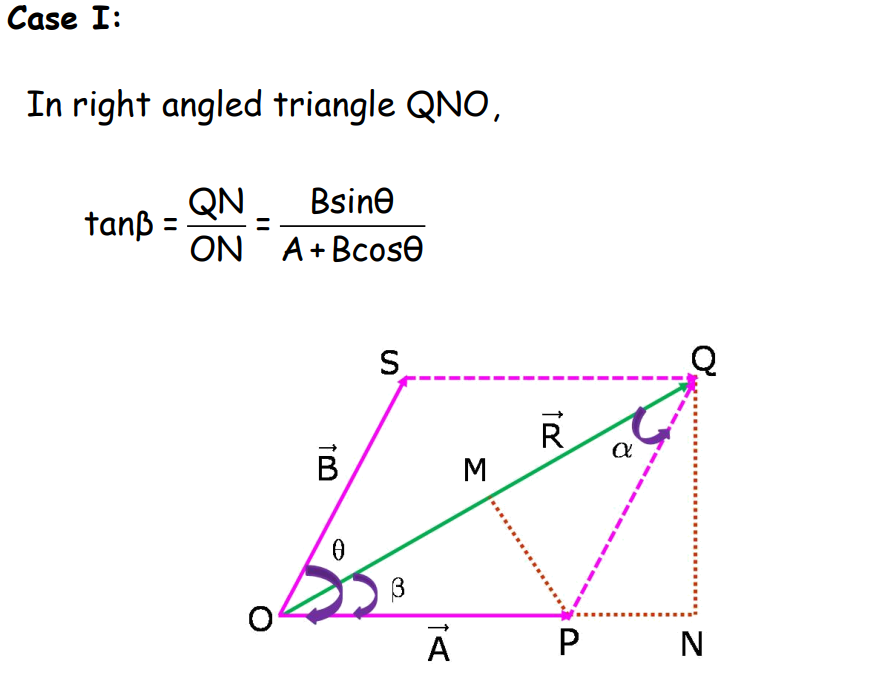
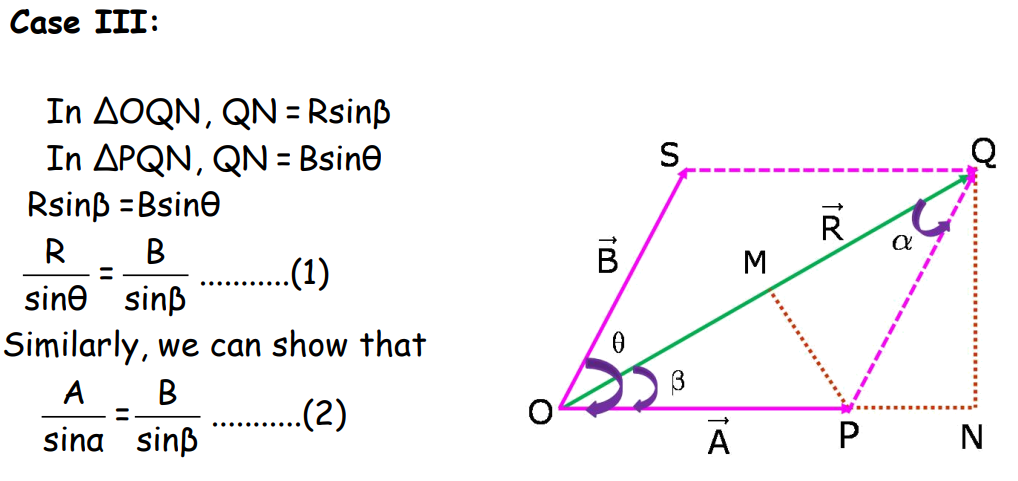
To Find the Direction of the Resultant Vector

In right-angled triangle QNO:

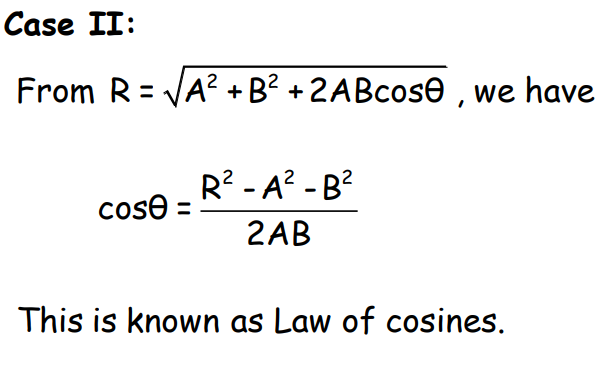
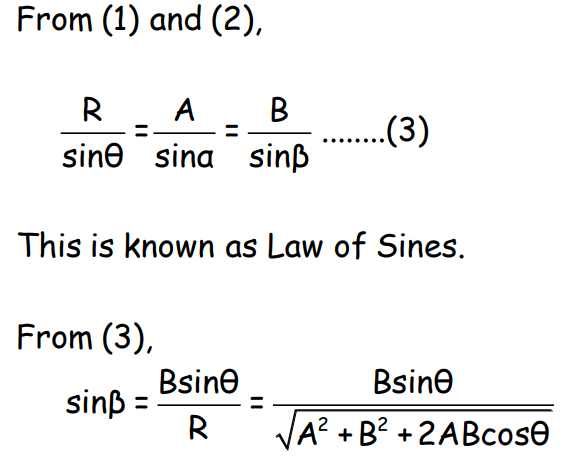
Polygon Law of Vector Addition

The Polygon Law states that if any number of vectors act on a particle simultaneously, their resultant is represented in magnitude and direction by the closing side of the polygon taken in the opposite order.

Polygon Law of Vector Addition

When four vectors AAA, BBB, CCC, and DDD are represented in magnitude and direction by the sides of a polygon (OP, PT, TS, SM), the resultant vector is obtained using the Polygon Law of Vector Addition.

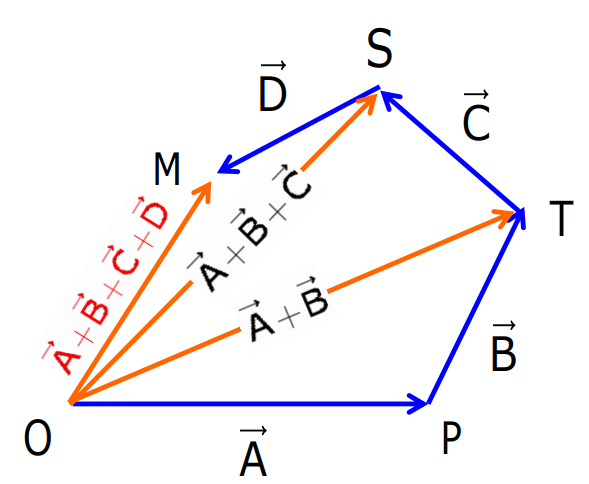
Resultant Vector:

A+B+C+D=R 

Where OM=R, the resultant vector.

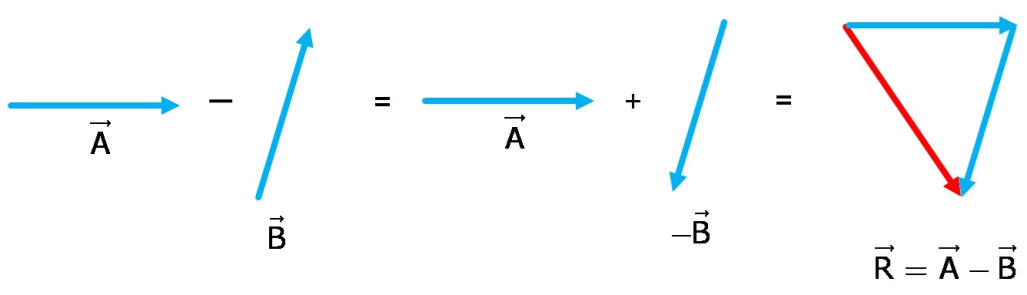
Subtraction of Vectors

The difference between two vectors is the sum of the first vector and the negative of the second vector.

Resolution of Vectors

Resolution is the process of splitting a single vector into two or more vectors in different directions, producing the same effect as the original vector. The vectors into which the original vector is split are called component vectors.

Rectangular Components of a Vector in 2D

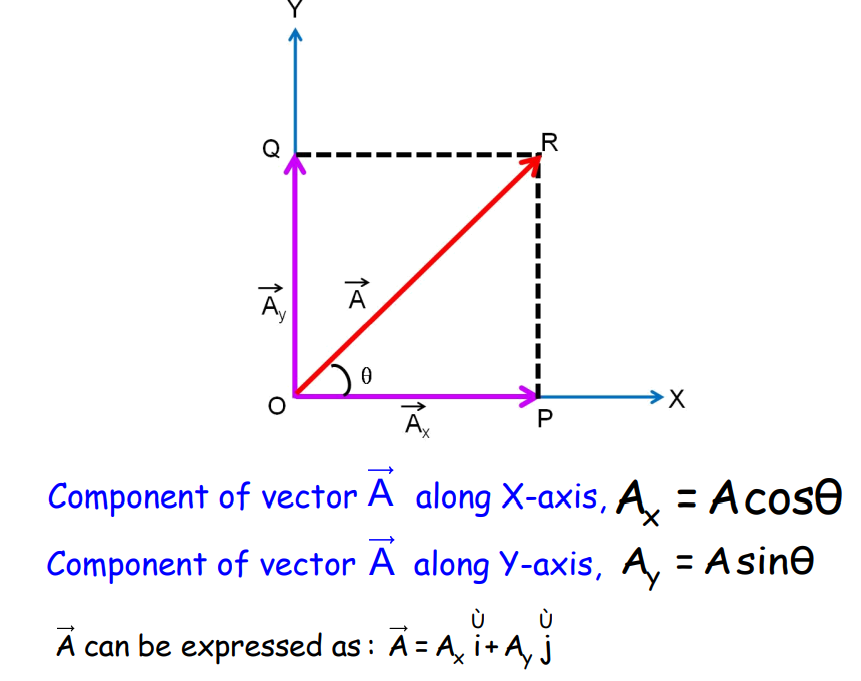
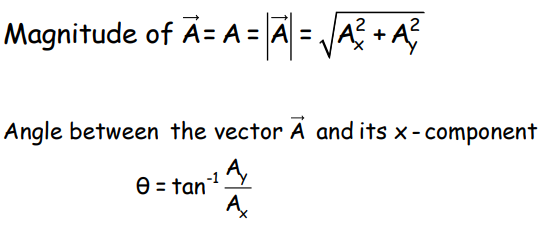
Rectangular Components of a Vector in 3D

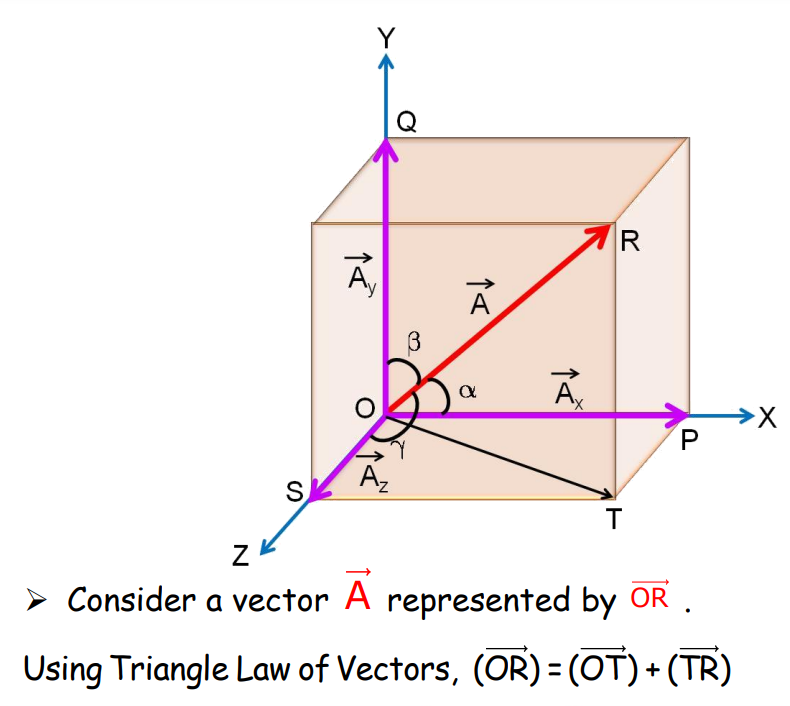
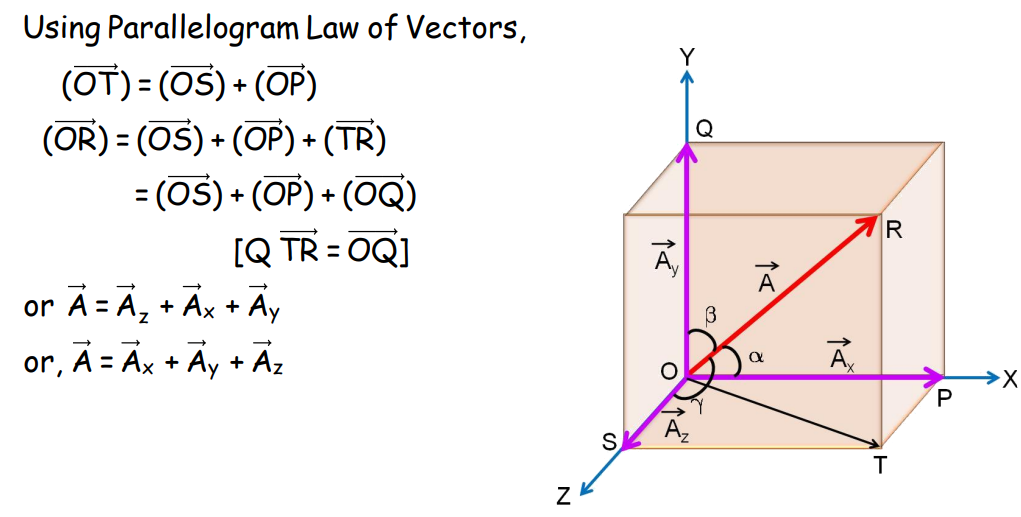
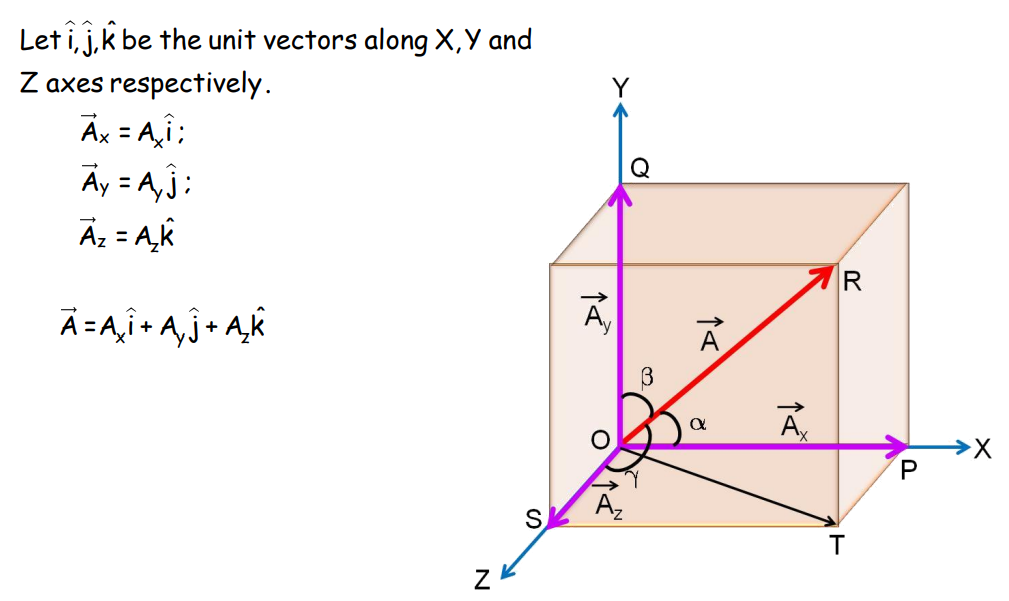
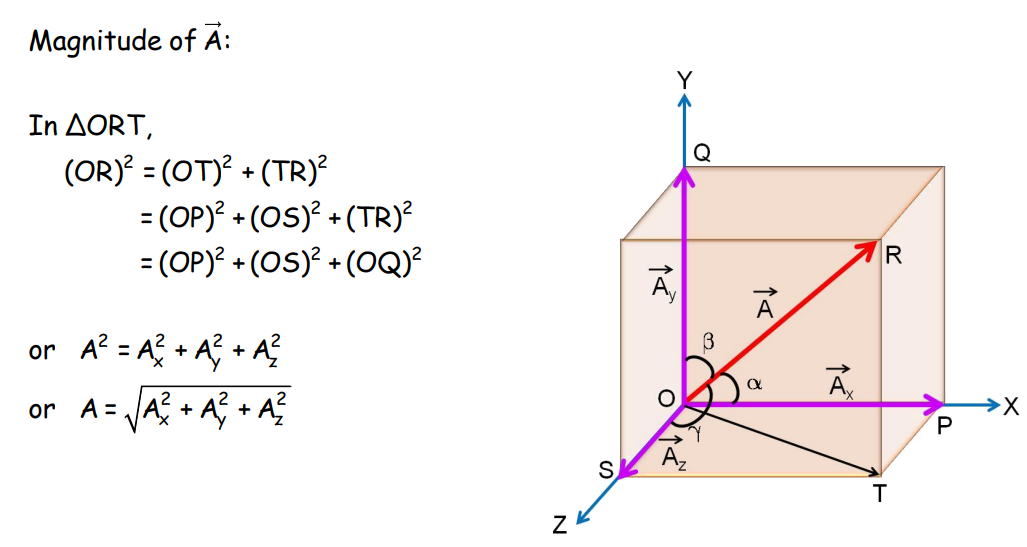
Analytical Method of Vector Addition

In the analytical method, the components of vectors A and B are added algebraically to find the resultant.

Motion in a Plane

In two-dimensional motion, the coordinates of the position of the object change with time. This can be analyzed as two simultaneous one-dimensional motions along perpendicular directions.

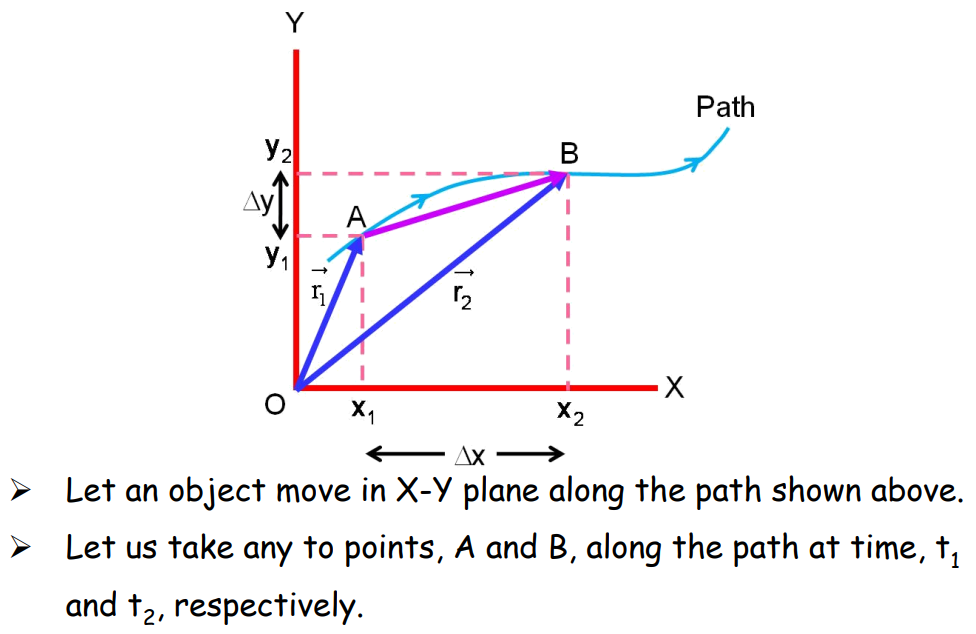
Position Vector & Displacement

• Position vectors at points A and B are given by:

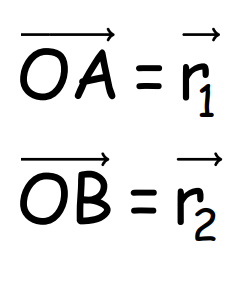
• Displacement: 

Velocity

• Average Velocity: It is defined as the total displacement of an object divided by the total time taken. It is a vector quantity, meaning it has both magnitude and direction. Mathematically, it can be expressed as:

Average Velocity = Total Displacement/Total Time

• Instantaneous Velocity:

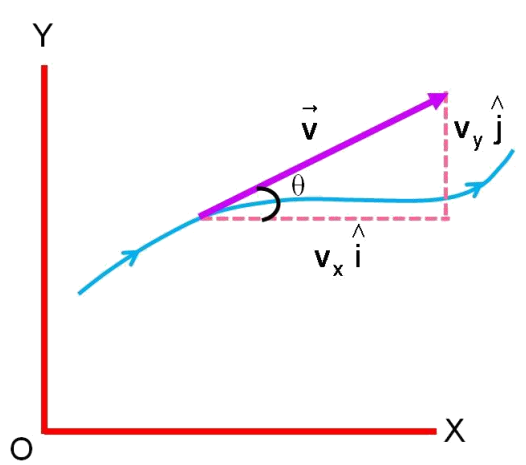
•  The magnitude of instantaneous velocity:

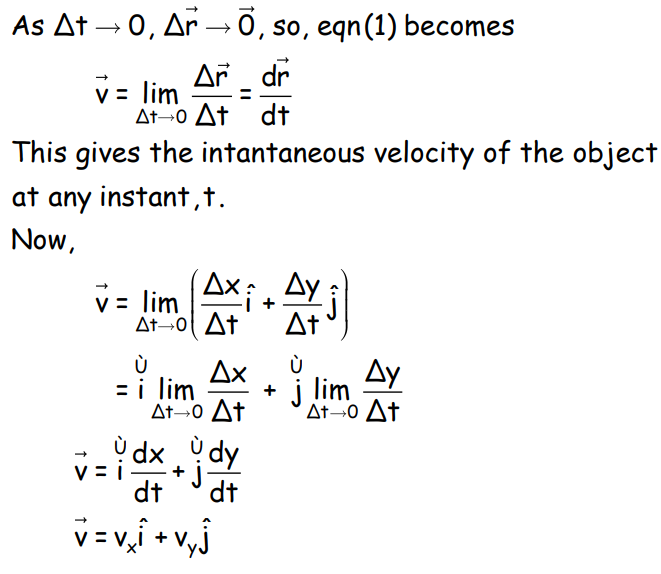
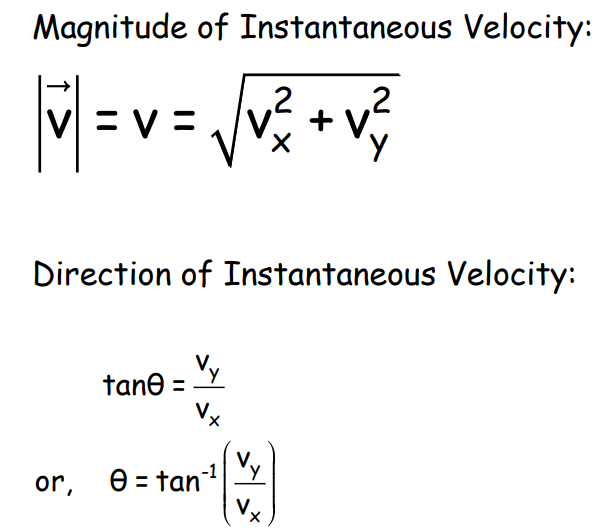
Acceleration

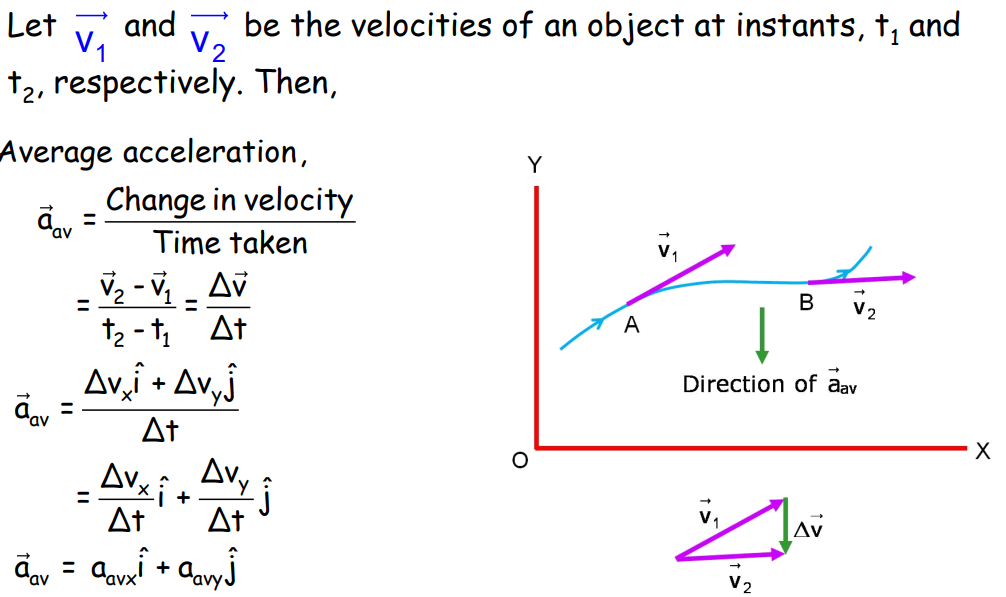
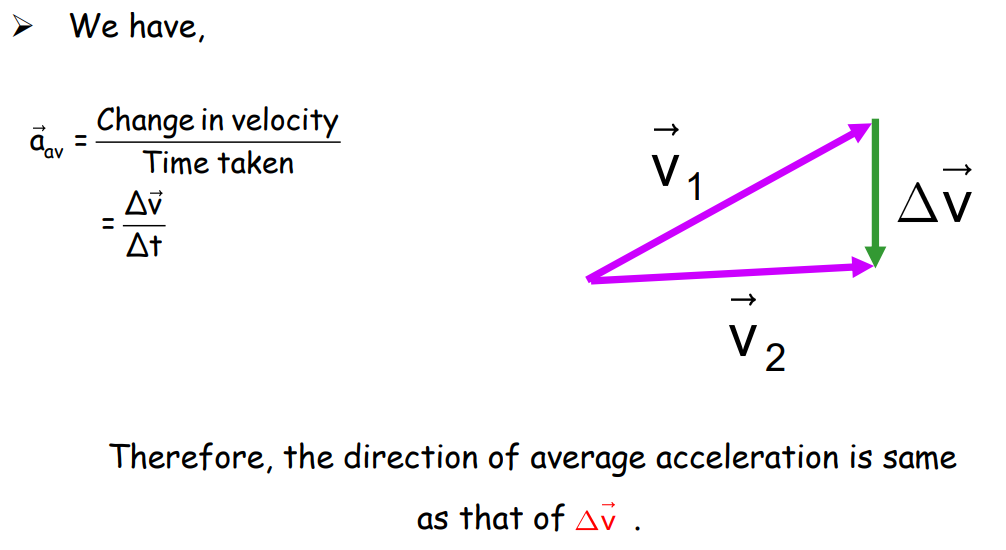
• Average Acceleration:

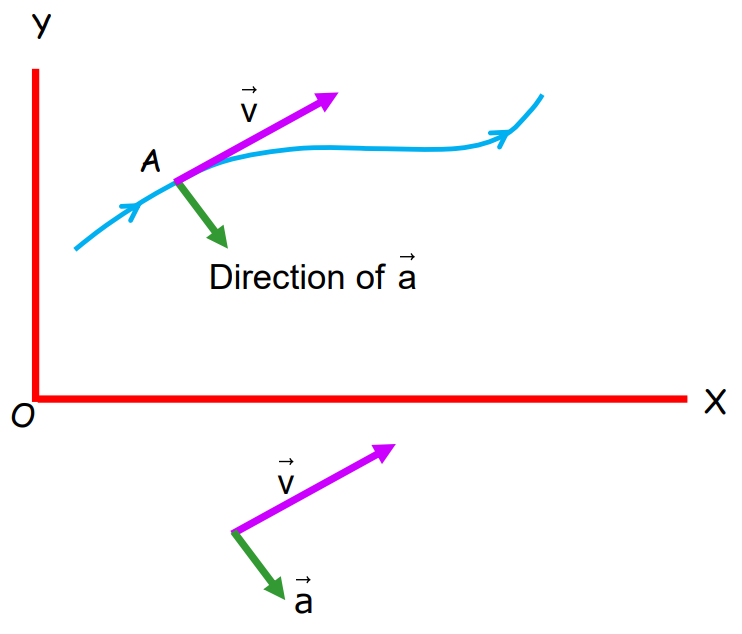
• Instantaneous Acceleration:

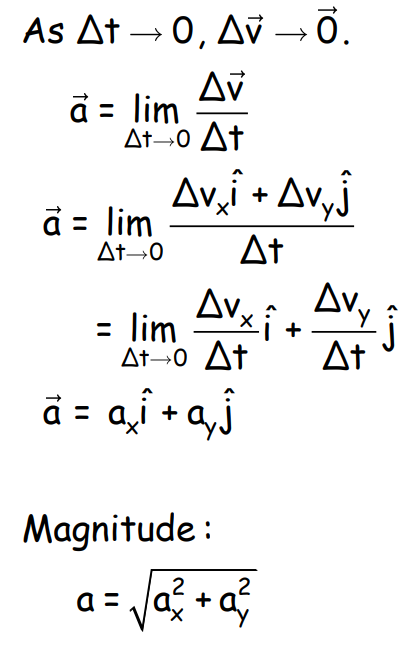
• Motion in Plane with Uniform Acceleration:

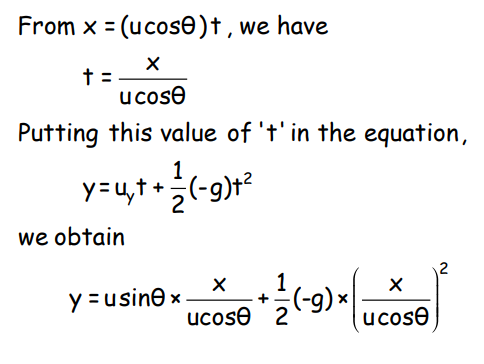
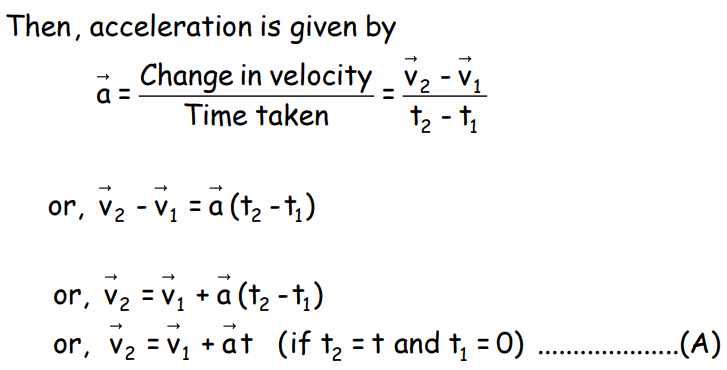
Relative  Velocity in 2D

Consider two bodies, A and B, moving with velocities va and vb, respectively, in a common frame of reference of two dimensions.                  

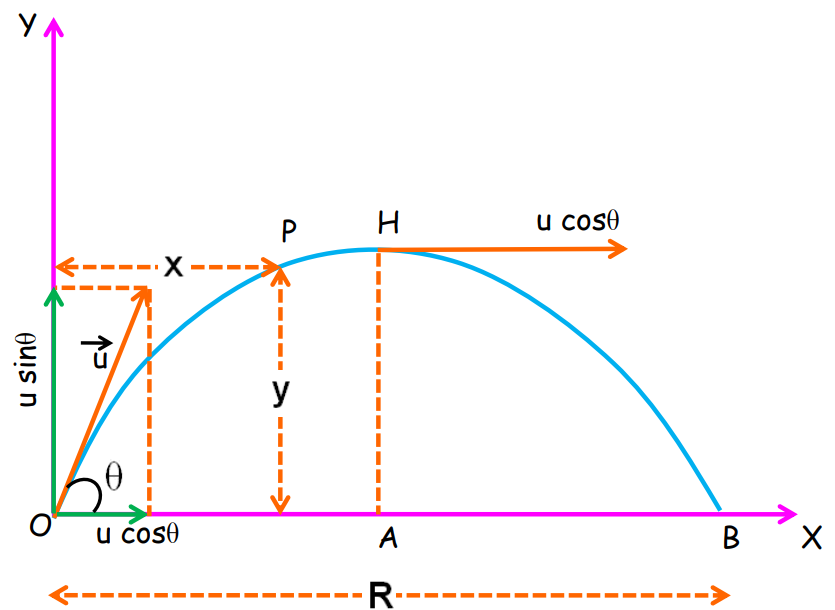
Projectile Motion

In projectile motion, an object is projected with an initial velocity and moves under gravity alone. The path of the projectile is a parabolic trajectory.

Horizontal Projection

• Horizontal Projection: An object is thrown with a non-zero initial velocity, along the horizontal direction. 
• Angular Projection: An object is projected with a non-zero initial velocity, making an angle, with the horizontal direction.

Few assumptions:

• Frictional air resistance is neglected.
• The effect due to the rotation of the earth and curvature is neglected.
• The value of g is constant in magnitude and direction at all points of the motion of the projectile.

Suppose, a ball is thrown horizontally from a tower with a velocity ux. At the time of projection, the vertical velocity is uy = 0.

The motion of the ball can be split into two components:

(i) Horizontal motion with constant velocity.

(ii) Vertically downward motion with constant acceleration (g).

• The horizontal velocity is constant because there is no horizontal component of acceleration. 
• Simultaneously, the magnitude of downward vertical velocity increases by 9.8 ms-1 after every second. 
• Thus, the projectile motion is a two-dimensional motion with constant acceleration.
• The time during which the ball remains in flight depends upon the downward motion alone. 
• The overall velocity of the ball changes continuously in both magnitude and direction. 
• Let vy be the magnitude of the vertical velocity of the ball at any time ‘t’. Then, the magnitude of the velocity of the ball at that time is given by 

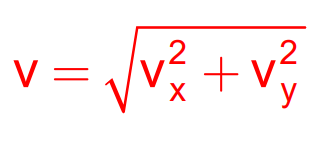
• Suppose v makes an angle β with the horizontal direction at that instant of time. Then

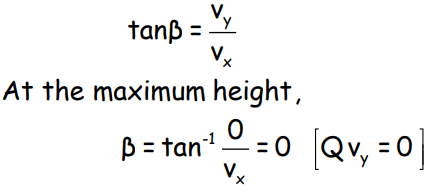
Projectile Given Angular Projection

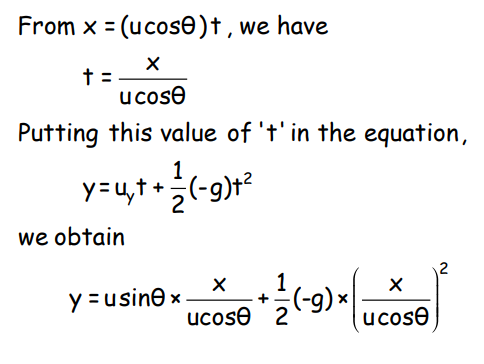
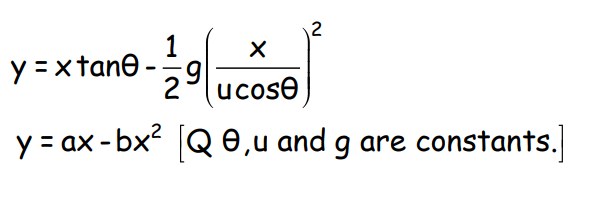
This is the equation of a parabola. Hence, a projectile follows a parabolic path.

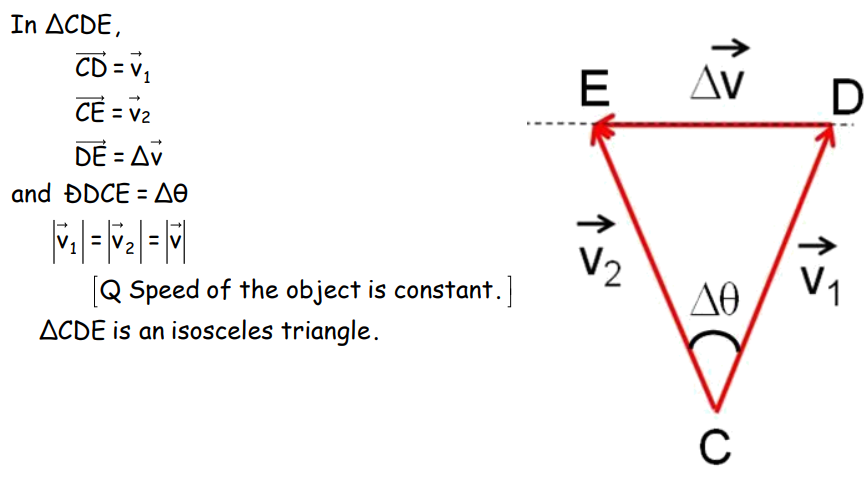
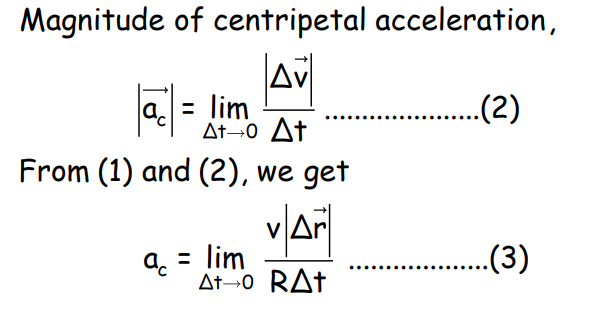
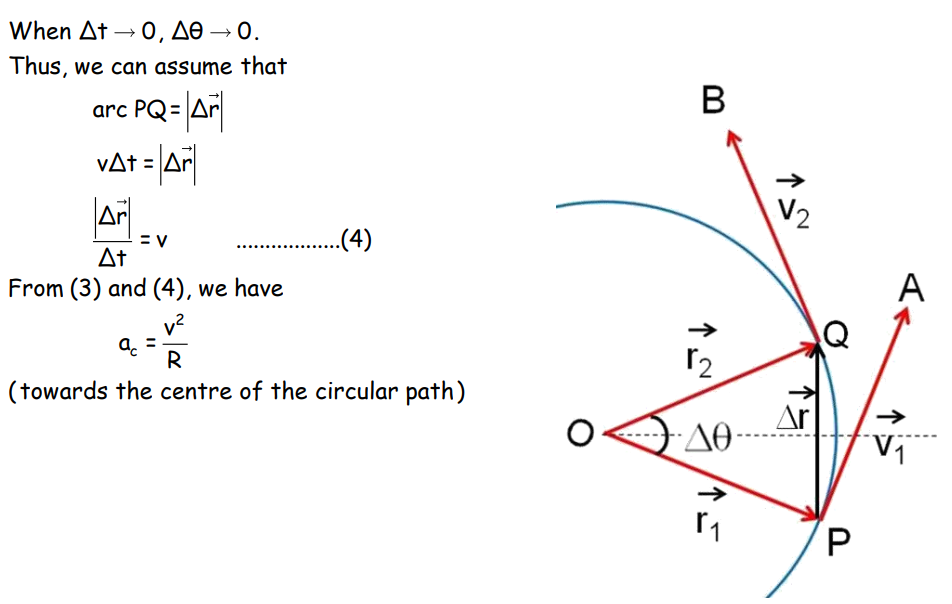
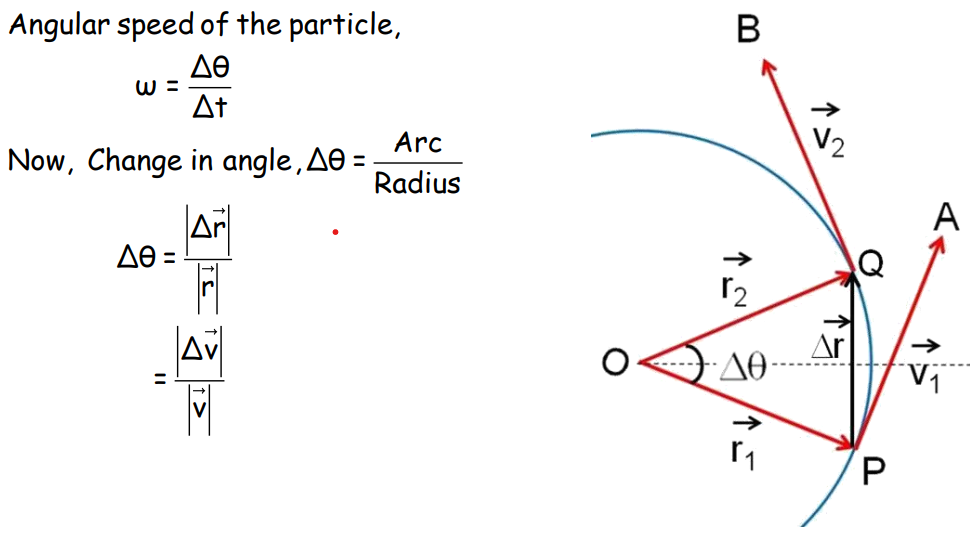
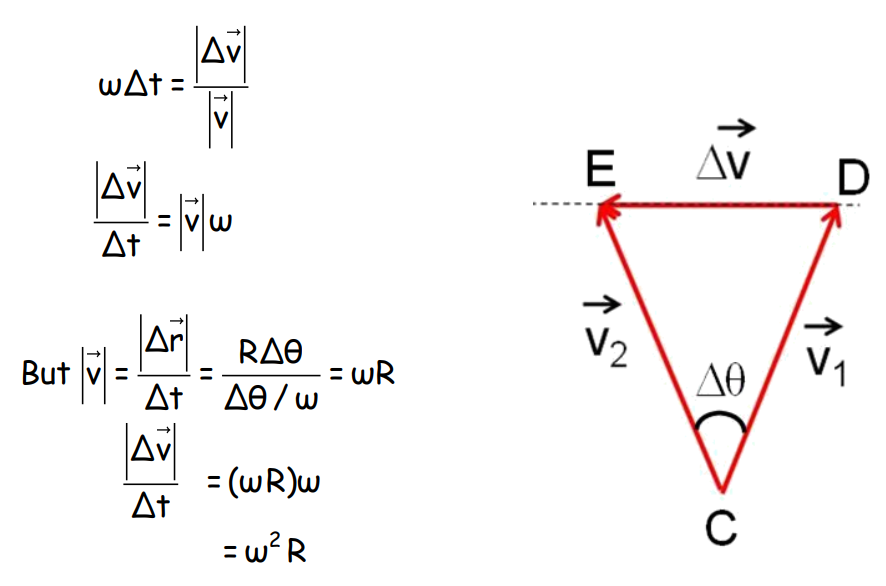
Uniform Circular Motion

In a uniform circular motion, an object moves with constant speed along a circular path. The velocity changes direction continuously, leading to centripetal acceleration.

Centripetal Acceleration

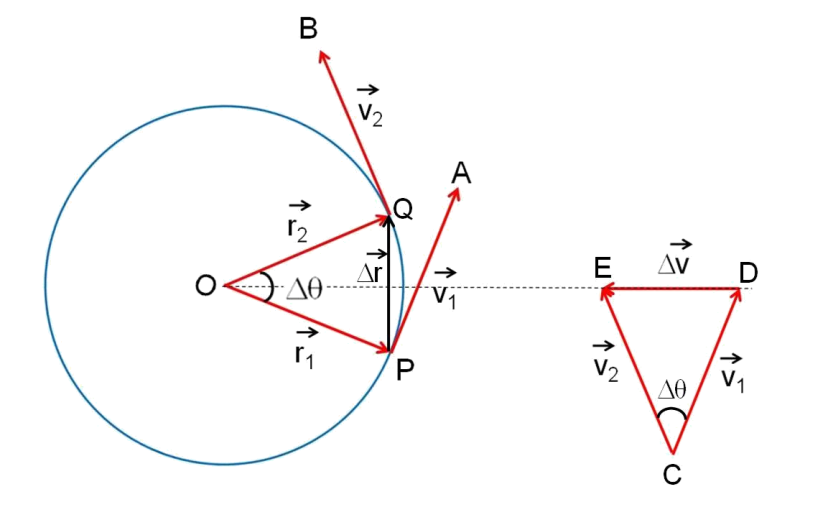
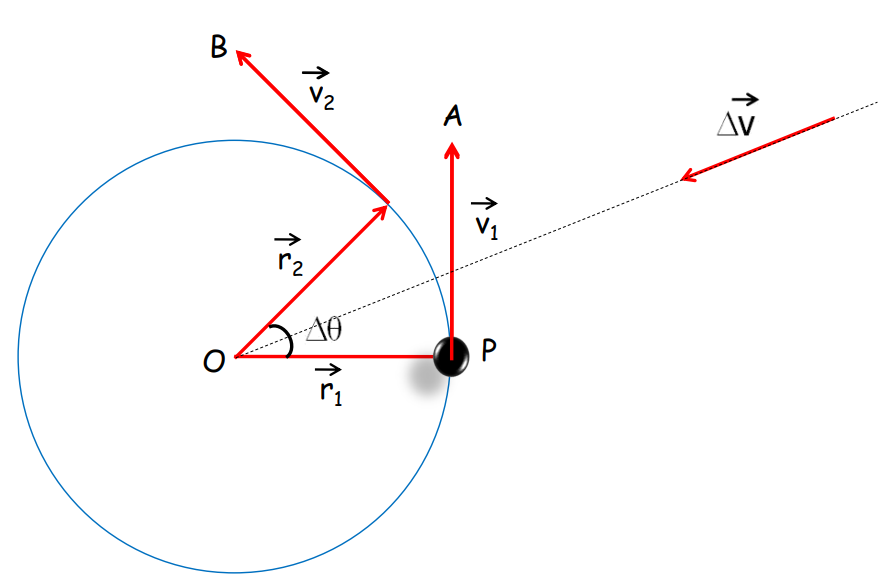
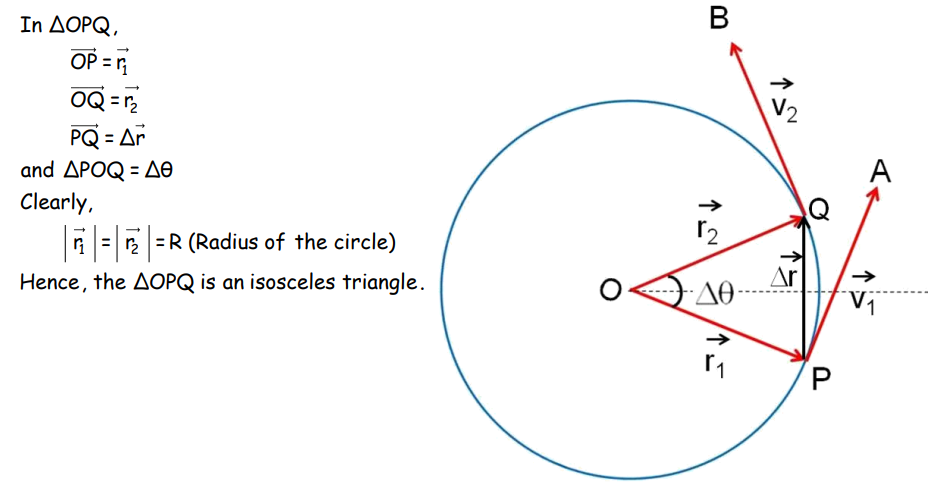
Where v is the speed and R is the radius of the circular path.

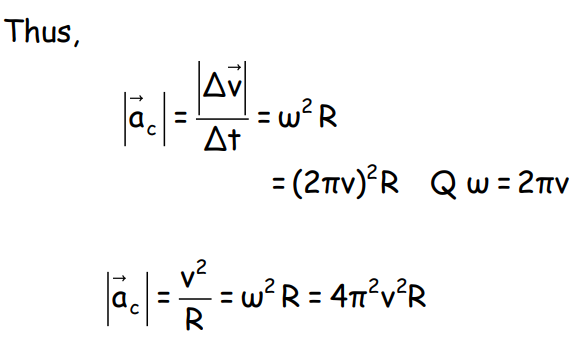
Conclusion

This comprehensive guide on “Motion in a Plane” provides an in-depth exploration of the fundamental aspects of physics as outlined in Class 11. It covers the core concepts of vector quantities, motion in two dimensions, and the application of vector algebra to describe motion. Topics include the resolution of vectors, projectile motion, and uniform circular motion. Additionally, the guide delves into the equations of motion under the influence of gravity, and how these principles are applied in real-world scenarios. The detailed explanations and diagrams help students understand the principles of motion in a two-dimensional plane effectively.