Differential Equations – Complete Guide For Class 12 Math Chapter 9

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Differential Equations in Mathematics for Class 12th are designed to ensure you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

The chapter on Differential Equations explores the techniques for solving equations involving derivatives of functions, which model real-world phenomena with continuous change. It introduces core concepts like the order and degree of differential equations and methods such as the separation of variables and integrating factors. Students learn to solve both ordinary and linear differential equations, apply them to problems in physics, engineering, and biology, and interpret solutions in practical contexts. The chapter underscores the significance of differential equations in describing dynamic systems and offers essential tools for analyzing and predicting changes in diverse fields.

Differential Equations

Differential equations are a fundamental concept in mathematics that helps us understand how quantities change over time. This chapter will guide you through the essential concepts, definitions, and methods used to solve differential equations.

Understand the Concept of Differential Equations

Imagine observing the replication of a type of bacteria in a culture. You might wonder:

If the replication process continues indefinitely, what will be the number of bacteria after 1 hour? After 2 hours?

If there are 350 bacteria at a certain time, how long will it take for the number to double?

To answer such questions, we introduce the concept of the differential coefficient.

Definition Of Differential Equation

A differential equation involves an independent variable, a dependent variable, and the differential coefficients of the dependent variable with respect to the independent variable. 

For instance, if N is the number of bacteria at time t, we might express its growth with: 𝑑𝑁/𝑑𝑡 = 2𝑁₀, where 𝑁₀ is the initial number of bacteria.

Order and Degree of Differential Equations

• Order: The order of a differential equation is the highest order derivative present in the equation.
• Degree: The degree is the power of the highest order derivative, provided the equation is a polynomial in derivatives.

Examples:

1. d³y/dx³ – 6dy²/dx² + 4dy/dx – y = 0 (Order 3, Degree 1)
2. (dy²/dx²)² + 3dy/dx – 2 = 0  (Order 2, Degree 2)

Linear Differential Equation

A differential equation is a linear differential equation if it is expressible in the form

dy/dx +Py = Q

Where P and Q are either constant or the functions of x only.

Example:

Differential Equation dy/dx+ y sin x =  cos x is linear, but ydy/dx xe^x  = 0 is non-linear differential equation as it contains product of dependent variable and its differential coefficient. 

Formation of Differential Equations

Consider the family of curves given by: y = e^mx Where m is a parameter. For different values of m we’ll have different curves of this family. 

Now, Differentiating y = e^mx with respect to x, we have 

dy/dx = me^mx

Eliminating parameter m gives dy/dx = my.

This is the differential equation of the family of curves represented by the equation y = e^mx . 

Note that we had a one-parameter family of curves. so, we differentiated the given equation only once. 

In general, if an equation of the n-parameter family is given, we differentiate the equation n times to obtain the differential equation of the family.

Example: 

Find the differential equation of all circles touching the x-axis at the origin.

Solution: 

The equation of the family of circles touching x-axis at the origin is given by: 

(x – 0)² + (y – a)² = a² or x² + y² – 2ay = 0 

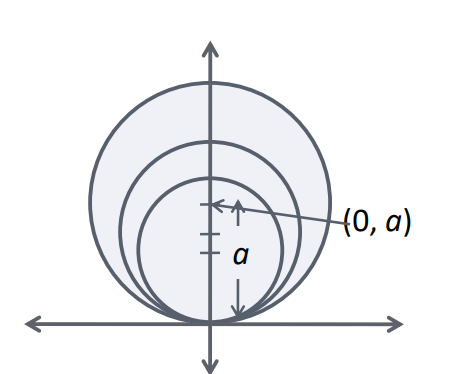
Given equation contains only one parameter namely ‘a’ so we’ll differentiate the given equation with respect to x once. We have,

2x + 2y dy/dx – 2a dy/dx = 0

⇒ a = x + y dy/dx / dy/dx

Substituting the value of a in the original equation, we have

 x² + y² – 2y (x + y (dy/dx)/(dy/dx))

Rearranging the above obtained equation, we get

 (x² – y²) dy/dx = 2xy

Which is the desired differential equation of family of circles. 

Solution of a Differential Equation

The solution of a differential equation is a relation between the variables involved which satisfies the differential equation. Such a relation and the derivatives obtained from there when substituted in the differential equation, makes left hand, and right hand sides identically equal. 

Example: 

Consider the function y = A cos x + B sin x and differential equation dy²/dx² + y = 0.

Differentiating the given function with respect to x, we have

dy/dx = – A sin x + B cos x

Differentiating above equation with respect to x again, we get 

dy²/dx² = – A cos x – B sin x

⇒ dy²/dx² = – y

⇒ dy²/dx² + y = 0 

Which shows that given function is a solution of given differential equation.

Type of Solutions of a Differential Equation 

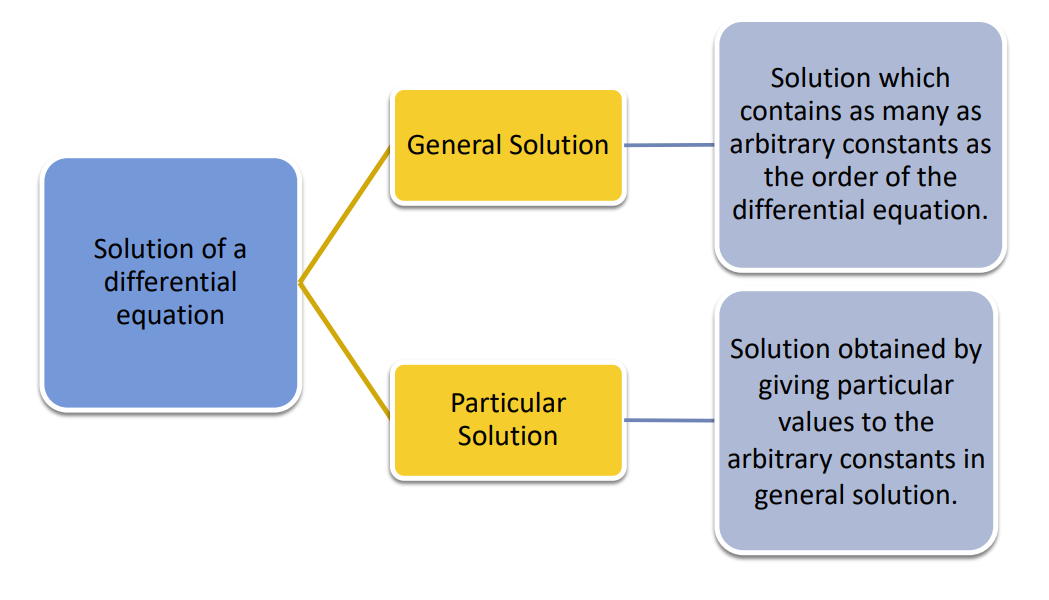
Example:

The function y = A cos x + B sin x is a general solution of the differential equation 

dy²/dx² + y = 0 

Whereas y = 2 cos x + 3 sin x is a particular solution of the same differential equation. 

Methods of solving Differential Equations

Example: 

Solve: dy/dx = x /x²+1

Solution: We have 

dy/dx = x /x²+1 ⇒ dy = x dx/x²+1

Integrating both sides, we get 

∫ dy = ∫x dx/x²+1 ⇒ ∫ dy = 1/2 ∫2x dx/x²+1

⇒ y = ½ log |x² +1| + C which is the solution of the given differential equation.

Example: 

Solve: dy/dx = sec y

Solution: We have dy/dx = sec y ⇒ dy/dx = 1/sec y

⇒ dx = 1 dy/secy ⇒ dx = cosy dy

Integrating both sides, we get 

∫dx = ∫cosy dy 

⇒ x = siny +C, where y ≠ (2n+1)/2 , n ∈ Z

Example: 

Solve: (x+1) dy/dx = 2xy

Solution: We have

(x+1) dy/dx = 2xy

⇒ dy/y = 2x dx /x+1 provided x ≠ -1 

Integrating both sides, we get

∫dy/y = 2∫(x+1-1) dx/x+1

⇒∫dy/y = 2∫(x+1-1) dx/x+1  = 2∫(1-1/x+1) dx

⇒ log y = 2(x- log|x+1|) + C

Example:

Solve: dy/dx = cos (x+y)

Solution: We have dy/dx = cos (x+y)

Let x+y = v

⇒ 1+ dy/dx = dv/dx

⇒ dy/dx = dv/dx -1

Putting x+y = v and dy/dx = dv/dx -1 in the given differential equation, we get 

dy/dx – 1 = cos v ⇒ dv/dx = 1+ cos v

⇒ 1dv/ 1+ cos v = dx

⇒ 1/2 sec² v/2 dv = dx

Integrating both sides gives

∫1/2 sec² v/2 dv = ∫1 dx

⇒  tan v/2 = x+C

Substituting back the value v = x+y in the obtained solution, we have 

Tan (x+y/2) = x + C.

Which is the desired solution of the given differential equation.

Homogeneous Function

A function f(x, y) is called a homogeneous function of degree n, if

f (x, y) = ⁿ f(x,y)

Example:

f(x, y) = x² – y² + 3xy is a homogeneous function of degree 2. Because we can write

f (x,y) = ²x² – ²y² + 3 x . y

               = ²x² – ²y² + 3 ²xy

               = ² (x² – y² + 3 xy)

                = ² f (x,y)

Homogeneous Differential Equations

If a first order first degree differential equation is expressible in the form

dy/dx = f(x,y)/g(x,y)

where f(x, y) and g(x, y) are homogeneous functions of the same degree, then the above differential equation is known as homogeneous differential equation.

Method of solving Homogeneous Differential Equations

Type I

Example: 

Solve: x²dy +y(x+y)dx = 0

Solution:

Rearranging the given differential equation, we get 

dy/dx = – (xy +y²/x²)

Since each of the functions xy + y²and x² is a homogeneous function of degree 2, therefore the given differential equation is homogeneous differential equation.

Putting y = vx and dy/dx = v+x dv/dx in given equation.

v +x dv/dx = – (vx² +v²x²/x²)

⇒ v+x dv/dx = – (v + v²)

⇒ dv/ v² + 2v = – dx/x

Integrating both sides, we get

∫ dv/v² + 2v = – ∫dx/x

⇒ ∫ dv/(v +1)² – 1² = – ∫dx/x

⇒ 1/2 log | v +1 – 1/v +1+1| = – log x + log C

⇒ log |vx²/v +2| = log k

|vx²/v +2| ⇒ |x²y/y +2x| = k  (y/x = v)

Type II

Example:

Solve: dy/dx – y/x = 2x², x > 0

Solution:

We have dy/dx – y/x = 2x², x > 0

⇒ P = 1/x and Q = 2x²

We have, I.F = e∫^Pdx = e∫^{1/x dx} = e⁻^{log x}  = e^{log x⁻¹}   = x⁻¹ = 1/x 

Now,

y . 1/x  = ∫ 2x² dx/x + C =  ∫2x dx + C

⇒ y/x = x² + C

⇒ y = x³ + Cx

Let’s Conclude

In conclusion, Differential Equations is a crucial chapter in the CBSE Class 12 Mathematics syllabus that provides students with a profound understanding of how to model and solve problems involving continuous change. Throughout this guide, we have covered essential concepts such as the order and degree of differential equations, various methods for solving them, and practical applications in real-world scenarios. The techniques explored, from the separation of variables to the use of integrating factors, are invaluable tools for analyzing dynamic systems in fields like physics and engineering.

As you engage with this chapter, remember that mastering Differential Equations not only enhances your mathematical skills but also equips you with the ability to approach complex problems with confidence. We encourage you to take advantage of iPrep’s comprehensive resources, including engaging animated videos, practice questions, and detailed notes, to solidify your understanding. With dedication and the right tools, you will excel in Differential Equations and be well-prepared for your exams and future studies. Embrace the journey of learning, and let Differential Equations pave the way for your success in mathematics!