Integrals – Complete Guide For Class 12 Math Chapter 7
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Integrals in Mathematics for Class 12th are designed to ensure you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.
The chapter Integrals delves into the core concepts of integral calculus, focusing on both indefinite and definite integrals. It introduces methods for evaluating integrals, such as substitution, integration by parts, and partial fractions. The chapter also covers the Fundamental Theorem of Calculus, which connects differentiation with integration. Additionally, it explores practical applications, including calculating areas under curves and solving problems involving the accumulation of quantities. By emphasizing the importance of integrals in various real-world scenarios, this chapter equips students with essential tools for advanced mathematical analysis and applications.
Integrals: Understanding the Fundamentals
Integrals form a crucial part of calculus, providing a method for calculating the area under curves and solving various problems in mathematics and applied sciences. This chapter introduces integrals through two main types: indefinite integrals and definite integrals. The indefinite integral, also known as the anti-derivative, reverses the process of differentiation, while the definite integral provides a precise area under a function’s graph.
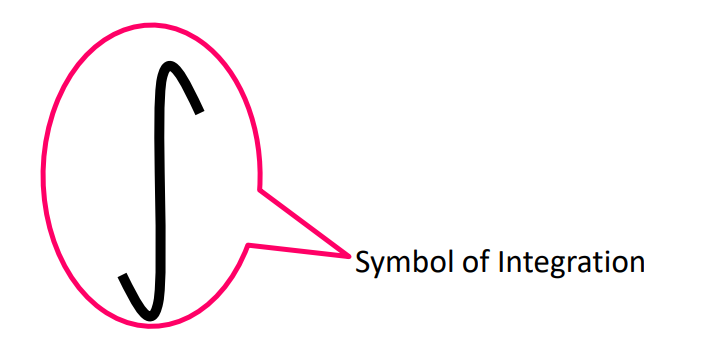
Symbol of Integration The symbol ∫ represents integration, similar to how differentiation is denoted by d/dx. A function Φ(x) is an integral of another function f(x) if Φ'(x) = f(x).
Example:
x⁴/4 is the integral of x³ as d/dx (x⁴/4) = 4x³/4 = x³
Meaning of Integral
Integration can be understood as the reverse process of differentiation.
It involves finding a function Φ(x) such that d(Φ(x))/dx = f(x).
The integration process is crucial in determining areas, and volumes, and solving differential equations.
The general form is ∫f(x) dx = Φ(x) + C, where C is the constant of integration, indicating there are infinitely many anti-derivatives for a given function, depending on the value of C.
Note: There exist infinitely many antiderivatives for each of these functions, which can be obtained by choosing C arbitrarily from the set of real numbers.
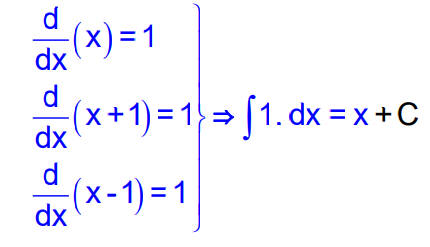
For this reason, C is customarily referred to as an arbitrary constant. C is the parameter by varying which one gets different anti-derivatives (or integrals) of the given function.
Terminology
There is a significant set of terminology mentioned in the chapter Integrals. These include-
Symbols/Terms Meaning ∫f(x) . dx A function F such that F(x) = f(x) f(x) in ∫f(x) dx Integrand x in ∫f(x) dx Variable of Integration Integrate Find the Integral An integral of f A function F such that f’(x) = f(x) Integration The process of finding the integrals Constant of Integrate (C) Any real number (C)
Standard Formulae for Integration
As per the chapter Integrals, several standard formulas facilitate the integration process:
- ∫xⁿdx = (xⁿ⁺¹/(n+1) + C, n ≠ –1
- ∫(1/x) dx = log|x| + C
- ∫exx dx = exx + C
- ∫axx dx = (axx)/(log a) + C
- ∫sin x dx = -cos x + C
- ∫cos x dx = sin x + C
- ∫tan x dx = log|sec x| + C
- ∫cot x dx = log|sin x| + C
- ∫cosec x dx = log|cosec x – cot x| + C
- ∫sec x . tan x dx = sec x + C
- ∫sec²x dx = tan x + C
- ∫cosec²x dx = -cot x + C
- ∫cosec x . cot x dx = -cosec x + C
- ∫sec x dx = log|sec x + tan x| + C
- ∫cosec x dx = log|cosec x – cot x| + C
- ∫1/√1 – x²dx = sin⁻¹x + C’ = -cos⁻¹x + C (since sin⁻¹x + cos⁻¹x = π/2)
- ∫1 /1 + x²dx = tan⁻¹x + C’ = -cot⁻¹x + C
- ∫ 1/√x² – 1 dx = sec⁻¹x + C’ = -cosec⁻¹x + C (since tan⁻¹x + cot⁻¹x = π/2 and sec⁻¹x + cosec⁻¹x = π/2)
Example:
Evaluate an Integral
Consider the integral ∫(x³ + 3x + 4) dx.
By integrating each term separately, we get:
∫x³ dx = (x⁴)/4, ∫3x dx = (3x²)/2, ∫4dx = 4x.
So, ∫(x³+ 3x + 4) dx = (x⁴)/4 + (3x²)/2 + 4x + C.
Integration and Differentiation
- Both are operations on functions.
- Every function is not differentiable or integrable.
- Both are inverses of each other.
- Both the operations are linear.
- Both processes involve limits.
- The constant can be taken outside the differential as well as the integral sign.
Integration versus Differentiation
Integration
1) Integration of a function is not unique.
2) It represents the family of curves having parallel tangents at the point of intersection of curves of the family with the lines orthogonal to the axis representing the variable of integration.
Differentiation
1) Differentiation of a function is unique.
2) It represents the slope of the tangent to the corresponding curve at that point.
Types of Integration
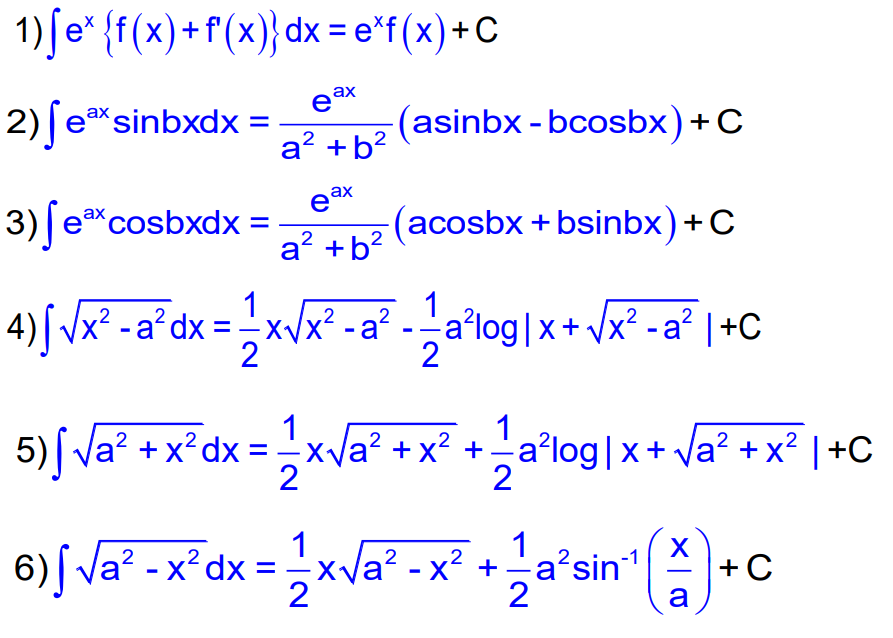
Integration Techniques Different techniques simplify integration, especially when dealing with complex functions:
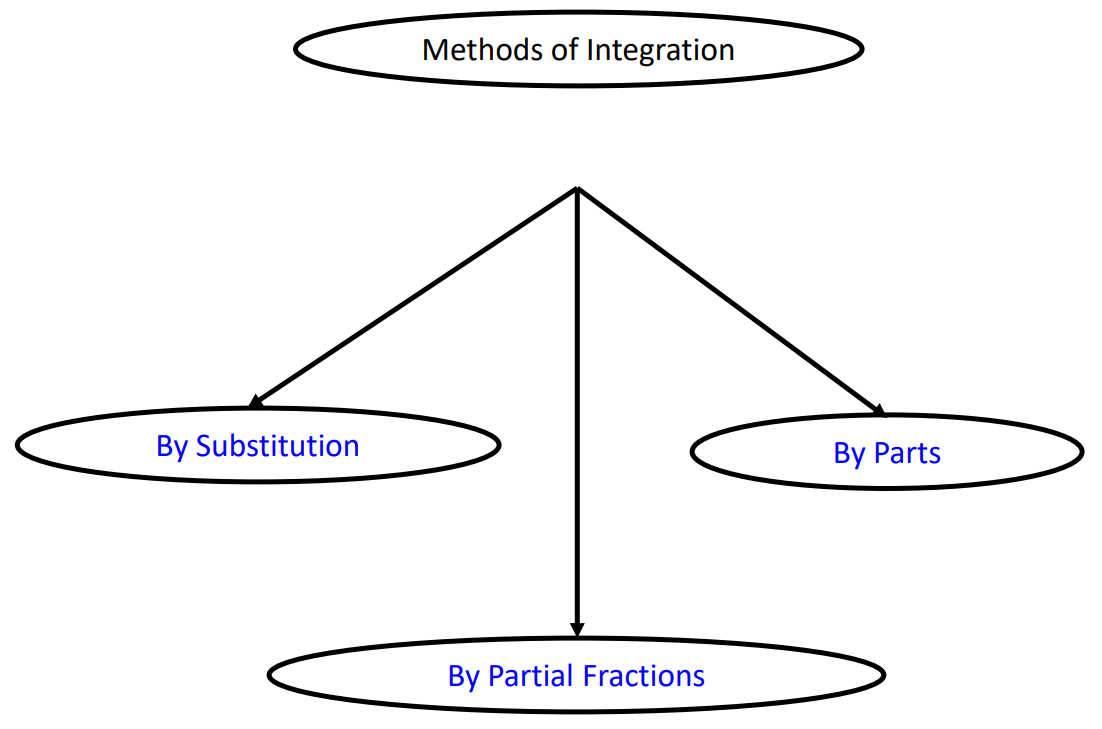
1. Substitution Method This involves changing the variable to simplify the integral.
The given integral can be transformed into another form by changing the independent variable x to t by substituting x = g (t). f(x) dx.
This change of variable formula is one of the important tools available to us in the name of integration by substitution.
For instance, to integrate ∫sec²x/(3 + tan x) dx, let t = 3 + tan x, then dt = sec²x dx, making the integral ∫(1/t) dt = log|t| + C = log|3 + tan x| + C.
Some Standard Substitution
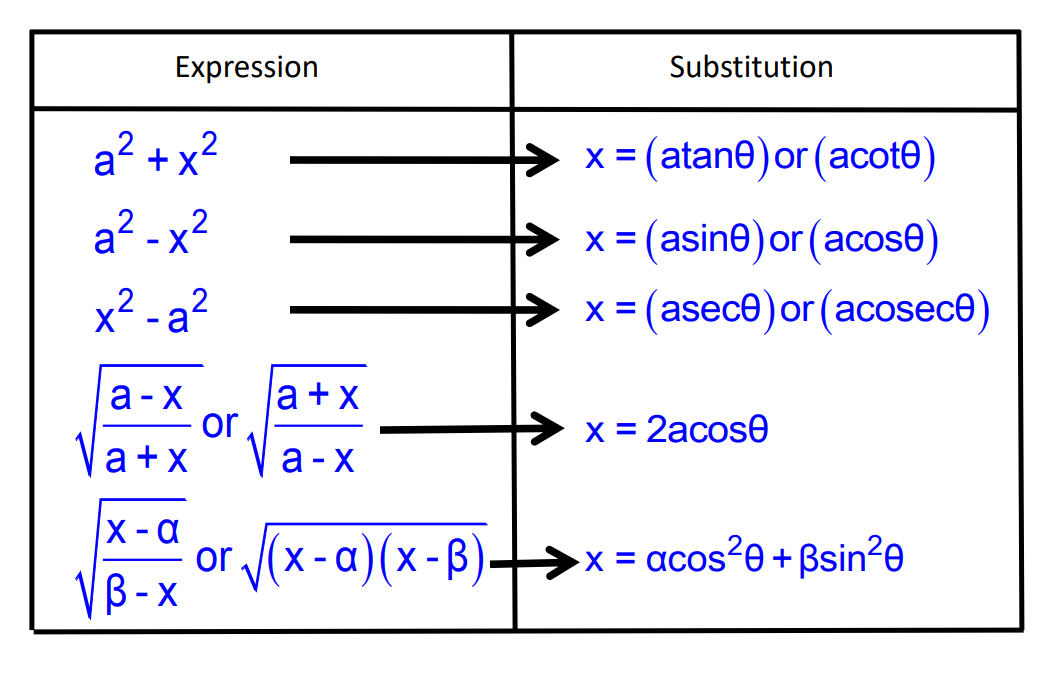
Integration using Trigonometric Identities
When the integrand involves some trigonometric functions, we use some known identities to find the integral.
Example: ∫cos²x dx = ∫1 + cos 2x / 2 dx
= 1/2∫dx +1/2 ∫ cos 2x dx
= x /2 + sin 2x /4 + C
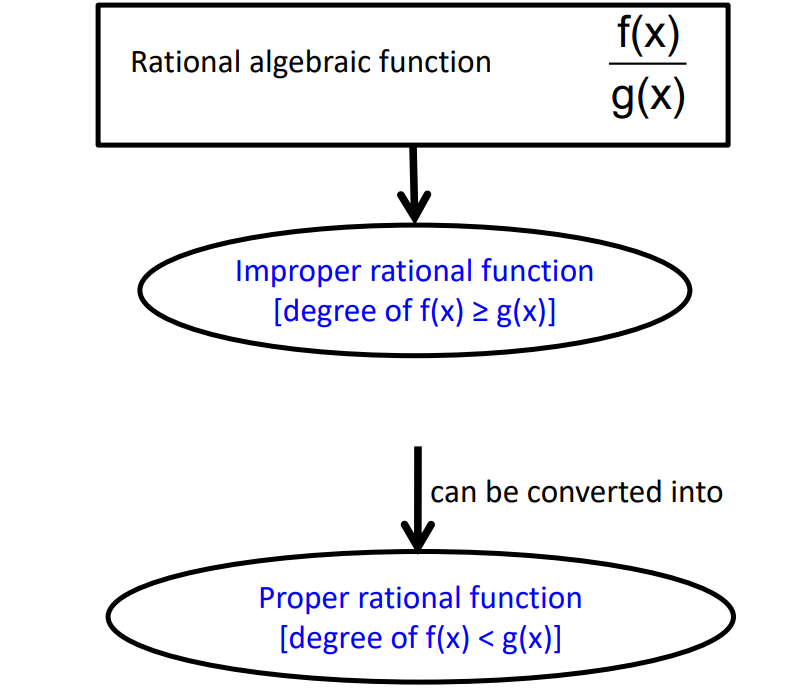
If, f(x)/g(x) is improper, then f(x)/g(x) = T(x) + f₁(x)/g(x)
where, T(x) is a polynomial in x and f₁(x)/g(x) is a proper rational function.
2. Partial Fractions This method decomposes a complex rational function into simpler fractions that are easier to integrate.
Any proper rational function f(x)/g(x) can be expressed as the sum of rational functions, each having a simple factor of g(x).
Each such fraction is called a partial fraction.
Integration by Partial Fractions
1) When the denominator is expressible as the product of non–reparing linear factors.
f(x)/g(x) = A₁/ x – a₁ + A₂/ x – a₂ + …….. + Aₙ/ x – aₙ
2) When the denominator is expressible as the product of the linear factors some of which are repeating.
f(x)/g(x) = A₁/ x – a + A₂/ (x – a)² + …….. + Aₖ/(x – a)ᵏ + B₁/ x – a₁ + B₂/ x – a₂ + …….. + Bₙ/ x – aₙ
3) When some of the factors of the denominator are quadratic but non–repeating.
f(x)/g(x) = Ax+B /ax²+bx+c + C₁/ x – a₁ + C₂/ x – a₂ + …….. + Cₙ/ x – aₙ
4) When some of the factors of the denominator are quadratic and repeating.
f(x)/g(x) = A₀(2ax+b)/ax²+bx+c + A₁/ax²+bx+c + A₁(2ax+b)/(ax²+bx+c)² + A₂ (ax²+bx+c)² +…………+ A₂ₖ₋₁ (2ax+b)/(ax²+bx+c)ᵏ + A₂ₖ/(ax²+bx+c)ᵏ
Example:
Integrate ∫(x – 1)/((x + 1)(x – 2)) dx
Solution: Let (x – 1)/(x + 1)+ (x – 2)
= A/(x + 1) + B/(x – 2)……..(i)
⇒ x – 1 = A (x -2) + B(x +1) …….(ii)
Putting x – 2 = 0 or x = 2 in (ii), we get
1 = 3B ⇒ B = 1/3
Putting x+1 = 0 or x = -1 in (ii), we get
-2 = -3A ⇒ A = 2/3
Substituting the values of and in, we get
(x – 1)/(x + 1)+ (x – 2) = 2/3. 1/x+1 + 1/3.1/x-2
Therefore, ∫(x – 1)/((x + 1)(x – 2)) dx = 2/3∫ dx/x+1 dx + 1/3∫dx/x-2
= 2/3 log |x+1| + 1/3 log |x-2| + C
3. Integration by Parts This technique is used when the integrand is a product of two functions. The formula is ∫u dv = uv – ∫v du.
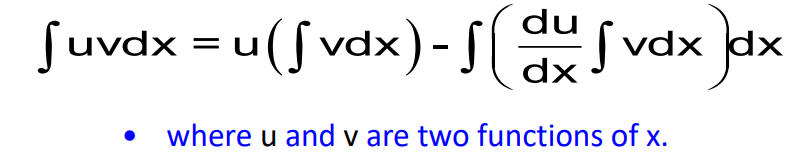
The choice of u and dv depends on the ILATE rule.
FIRST FUNCTION is the one which comes first in the word ILATE, where
I – Inverse trigonometric functions.
L – Logarithmic functions.
A – Algebraic functions.
T – Trigonometric functions.
E – Exponential functions.
Some Important Results
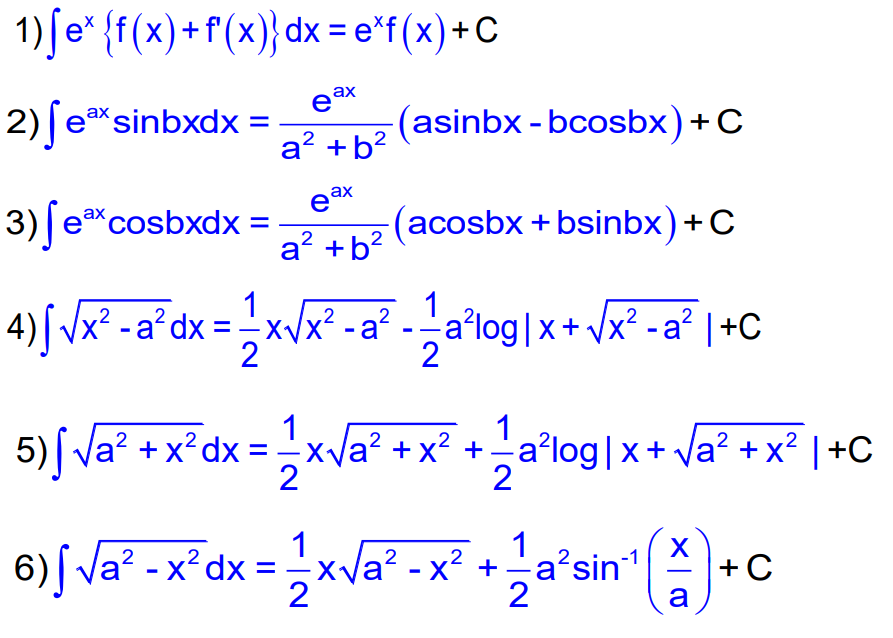
Example:
∫x³ log 2x dx = (log 2x). x⁴/4 – ∫1/2x. 2. x⁴/4 dx
= x⁴/4 (log 2x) – 1/4 ∫x³ dx
= x⁴/4 (log 2x) – 1/16.x⁴+C
Solutions of Integral of some Standard Form
∫x²+1 dx/ x⁴ + λx² +1, ∫x²-1 dx / x⁴ + λx² +1 & ∫dx/ x⁴ + λx² +1
Divide numerator and denominator by x²
Express the denominator of the inegrand in the form of
(x + 1/x)² ± k²
Introduce d (x + 1/x) or d (x – 1/x) or both in the numerator.
Substitute (x + 1/x = t) or (x – 1/x = t) as the case may be and proceed.
∫∅(x)/P√Q
If, P & Q both are linear functions of x, then
Put Q = t²
If, P is a quadratic expression & Q is a linear expression of x, then
Put Q = t²
If, P & Q both are pure quadratic expressions of x, then
Put Q = 1/t
If, P is a linear expression & Q is a quadratic expression of x, then
Put Q = 1/t
Example: ∫ 1dx /(x-3) √ x +1
Let I = ∫ 1dx /(x-3) √ x +1
Here, P and Q both are linear, so we substitute Q = t²
That is x + 1 = t² and dx = 2t dt
⇒ I = ∫1dt/(t²- 1-3) 2t /√ t²
= 2 ∫ dt/ (t²- 2²) = 2.1/ 2(2) log |t-2/t+2| + C
= 1/2 log |√x+1-2 / √x+1+2| +C
Also, understand the integral of the form
- ∫ sin mx cos nx dx = ∫ sin mx sin nx dx = ∫ cos mx cos nx dx
Multiply by 2 & use:
2sinAcosB = sin(A +B)+ sin(A -B)
2cosAsinB = sin(A +B)- sin(A -B)
2cosAcosB = cos(A +B)+cos(A -B)
2sinAsinB = cos(A -B)- cos(A +B)
- ∫1dx/ax²+bx+c = ∫1dx/√ax²+bx+c
Make the coefficient of x²unity & use completing the squares method. Then solve.
∫(px +q)dx/ax²+bx+c = ∫(px+q)dx/√ax²+bx+c
Put px + q = λ (ax²+bx+c) d/dx +
∫1 dx/ a sin²x + b cos²x = ∫1 dx/ (a sinx + b cosx)²
∫1 dx/ a + b cos²x & ∫1 dx/ a + b sin²x + c cos²x
Divide numerator & denominator by cos²x. Put sec²x = 1+ tan²x, if any. then substitute tan x = t & solve.
∫ dx / a sinx + b cos x, ∫ dx / a + b cos x,
∫ dx / a + b sin x, ∫ dx / a + b sinx + c cos x,
Put sin x = 2 tan x/2 / 1 + tan²x/2, cos x = 1 – tan²x/2 / 1 + tan²x/2 and replace sec²x /2 in numerator by 1 + tan²x/2 and put tan x /2 = t
∫a sin x + b cos x dx / c sin x + d cos x
Put a sin x + b cos x = λ d /dx (c sin x + d cos x) + (c sin x + d cos x )
∫a sin x + b cos x + c dx / p sin x + d cos x +r
a sin x + b cos x + c = λ d /dx (p sin x + q cos x + r) + (p sin x + q cos x + r) + v
Example:
Evaluate: ∫ (x³ + x + 1) dx/ x² – 1
I = ∫x + (2x + 1) dx/x² – 1 (after division)
I = ∫x dx + ∫2x dx/x² – 1 + ∫1 dx /x² – 1
= x² /2 + log | x² -1| + 1/2 log |x -1/x +1| + C
Definite Integral
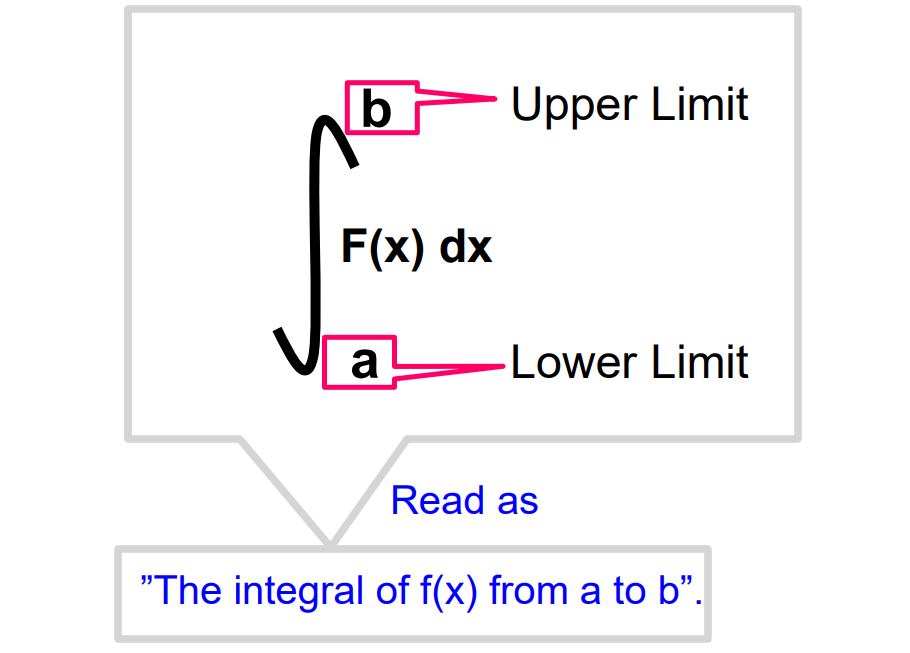
Definition: The definite integral of f(x) over [a,b] is denoted by abf(x)dx is equal to ∅(b) – ∅(a) i.e.
abf(x)dx = ∅(b) – ∅(a)
Fundamental Theorem of Integral Calculus
Let ∅(x) be the primitive or anti-derivative of a continuous function f(x) defined on [a, b] i.e. d/dx (∅(x)) = f(x). Then the definite integral of over [a, b] is denoted by abf(x)dx and is equal to ∅(b) – ∅(a).
Algorithm for Evaluation of Definite Integrals
The value of abf(x) dx can be calculated as: –
- Find the indefinite integral f(x) dx. Let this be ∅(x).
- Evaluate ∅(b) & ∅(a).
- Calculate ∅(b) – ∅(a). This is the required value.
Evaluation of Definite Integrals by Substitution
The method of evaluating an integral by reducing it to standard form by a proper substitution is called integration by substitution.
Substitution is made in the
- integrand.
- Differential (for example dx).
- Limits.
Properties of Definite Integrals
- abf(x) dx = abf(t) dx
- -aaf(x) dx = 2abf(x) dx, if f(x) is an even function,
and 0, if f(x) is an odd function.
- a2af(x) dx = 20af(x) dx, where [f (2a-x) = f(x)]
and 0, where [f (2a-x) = -f(x)]
- 0af(x) dx = 0af(a-x) dx
- abf(x) dx = -baf(x) dx
- abf(x) dx = acf(x) dx + cbf(x) dx; a < c < b
- abf(x) dx = abf(a+b-x) dx
Definite Integral as the Limit of a Sum
abf(x) dx = h0h [f(a) + f(a+h)……..+ f(a+(n-1)h]
abf(x) dx = (b-a)h01/n [f(a) + f(a+h)……..+ f(a+(n-1)h]
Where, h = b-a/n →0 as n →∞
The definite integralabf(x) dx is the area bounded by the curve y = f(x) with ordinates at x = a, x = b, and x-axis, i.e. h∞ Sₙ = abf(x) dx
Example:
Evaluate: 12(x² + 3x -5) dx
12(x² + 3x -5) = x³/3 + 3. x²/2 – 5x|²
= [2³/3 + 3. 2²/2 – 5.2] – [1³/3 + 3.1²/2 – 5.1]
= 11/6
Let’s Conclude
In conclusion, the chapter Integrals is a cornerstone of CBSE Class 12 Mathematics, equipping students with vital skills for mastering integral calculus. Through a thorough exploration of both indefinite and definite integrals, learners gain insights into essential techniques such as substitution, integration by parts, and partial fractions. The practical applications discussed, including the calculation of areas under curves, further highlight the importance of integrals in solving real-world problems.
By utilizing iPrep’s comprehensive learning resources, including engaging animated videos and practice questions, students can enhance their understanding of the chapter Integrals and develop a strong mathematical foundation. Remember, mastering this chapter is not only crucial for academic success but also serves as a valuable tool in various fields of study and professional applications. Embrace the journey of learning integrals, and let the knowledge you gain here pave the way for your future mathematical endeavors!
Explore our resources for the chapter Integrals to ensure you’re well-prepared for any challenge ahead by downloading iPrep Today.
Practice questions on Chapter 7 - Integrals
Get your free Chapter 7 - Integrals practice quiz of 20+ questions & detailed solutions
Practice Now








