Relations and Functions – Complete Guide For Class 12 Math Chapter 1
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Relations and Functions in Mathematics for Class 12th are designed to ensure that you grasp this concept with clarity and perfection. Whether studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best integrated learning with interesting explanations and examples.
The chapter Relations and Functions delves into the foundational concepts of relations and functions, which are crucial in understanding the mathematical relationships between different sets. Students learn to define relations, domain, range, and functions, and distinguish between different types of functions, such as one-one, onto, and inverse functions. The chapter also covers key concepts like composite functions and the algebra of functions. Understanding these topics is essential for solving complex problems in calculus and other advanced areas of mathematics, as they form the basis for analyzing and interpreting mathematical models.
Relations and Functions
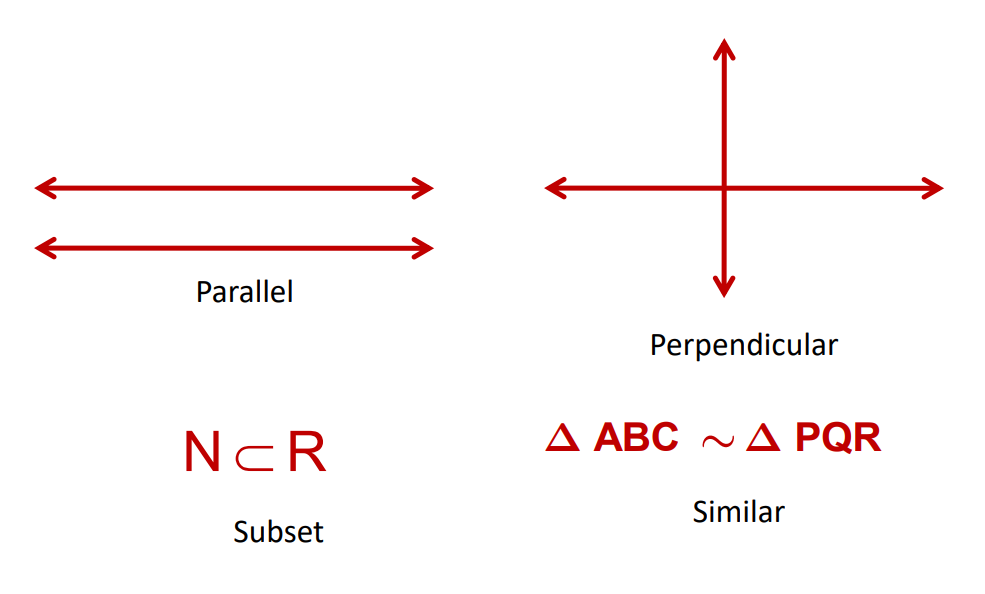
In our daily lives, we encounter various relations and functions, such as the relationship between a mother and daughter or a father and son. These are examples of relations in a non-mathematical sense. Similarly, in mathematics, we come across different types of relations, such as subsets, perpendiculars, parallels, and similarities. The figure shows the relations of perpendicular, parallel lines, subset, and similarity:
Understanding Ordered Pairs
An ordered pair consists of two elements in a fixed order, represented as (a,b), where a is the first component and b is the second component. For example, in the context of countries and their capitals, we can represent them as ordered pairs like (India, Delhi), (Japan, Tokyo), and (Italy, Rome).
Cartesian Product
The chapter – relations and Function significantly cover cartesian products. This involves-
If A={a,b} and B={1,2,3}, then the Cartesian product A×B is defined as: A×B={(a,1),(a,2),(a,3),(b,1),(b,2),(b,3)}
The Cartesian product of two non-empty sets A and B is denoted by A×B.
Relations
Let A and B be two non-empty sets. A relation R from set A to set B is a subset of A × B.
R ⊆ A × B
This subset is derived by describing a relationship between the first and second elements of the ordered pairs in A × B. The second element is known as the image of the first element.
Types of Relations
There are various types of relations mentioned in the chapter relations and functions. These include-
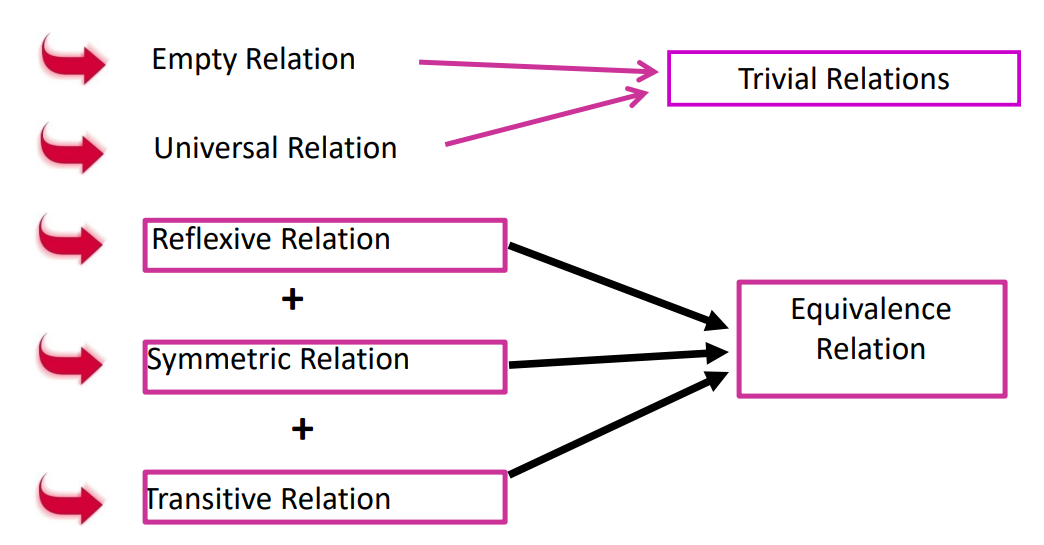
- Empty Relation: If no element of A is related to any element of A, i.e., R = ∅ ⊂ A x A, then R is said to be an empty or void relation.
For example, if A={1,2,3,4} and R={(a,b)∈R:a−b=10}, then R is an empty relation as a−b ≠ 10 for all a b∈A.
- Universal Relation: If each element of A is related to every element of A, i.e., R = A x A, then R is a universal relation.
For example, for the set A={1,2,3,4,5}, R={(a,b)∈R:a−b≥0} is a universal relation on set R.
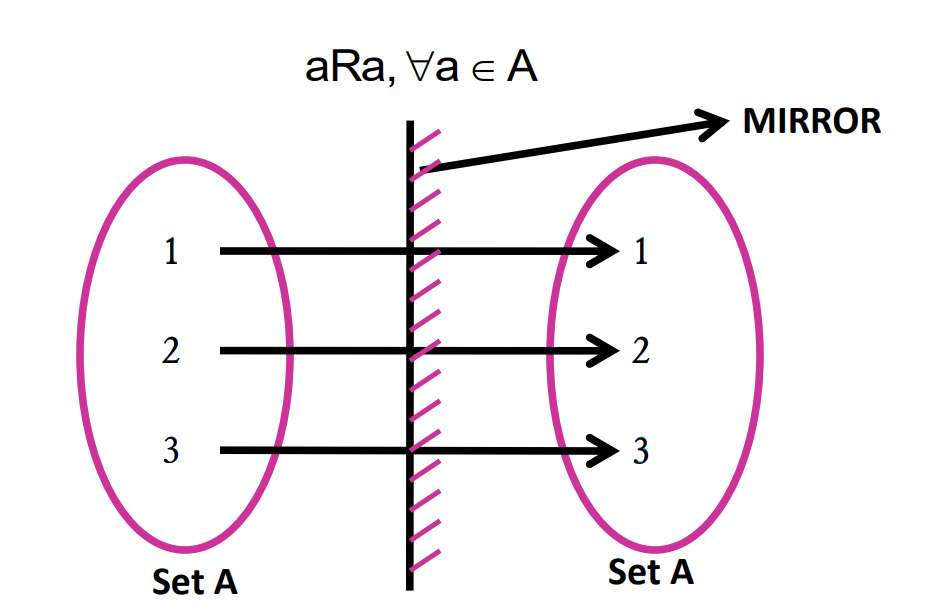
- Reflexive Relation: A relation R is reflexive if (a,a)∈R for every a∈A. This means each element is related to itself.
- Symmetric Relation: A relation R is symmetric if (a,b)∈R implies (b,a)∈R for all a b∈A.
In other words, If elements in set A are related to elements in set B, then elements in set B are also related to elements in set A by the same relation.
aRb ⇒ bRa, ∀a∈A, b∈B
- Transitive Relation: A relation R is transitive if (a,b)∈R and (b,c)∈R implies (a,c)∈R for all a,b,c∈A.
Elements of A are related to elements of B, and elements of B are related to elements of C then elements of A are also related to elements of C by the same relation.
For if a=b and b=c, then a=c.
aRb and bRc ⇒ aRc, ∀a∈A, b∈B and c∈C
Example: Which of the following relations are transitive relations?
i) ‘is equal to’ relation ii) ‘is greater than’ relation iii) ‘is less than’ relation
Explanation:
i) ‘is equal to’ relation a = b and b = c ⇒ a = c, ∀a∈A, b∈B, c∈C
ii) ‘is greater than’ relation a > b and b > c ⇒ a > c, ∀a∈A, b∈B, c∈C
iii) ‘is less than’ relation a < b and b < c ⇒ a < c, ∀a∈A, b∈B, c∈C
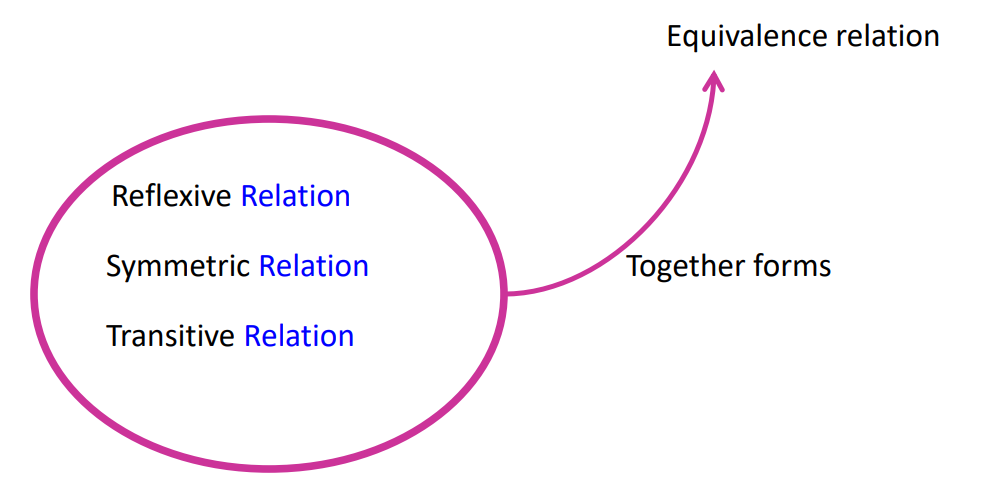
- Equivalence Relation: A relation R is an equivalence relation if it is reflexive, symmetric, and transitive.
Example:
If Tis the set of all triangles in a plane with a relation ‘is similar to’ then this relation is an equivalence relation, because every triangle is similar to itself (reflexive), and if one triangle is similar to another, the reverse is also true (symmetric).
Moreover, if triangle △ABC is similar to △PQR, and △PQR is similar to △DEF, then △ABC is similar to △DEF (transitive).
For any three triangles ABC, PQR and DEF :
ΔABC : ΔPQR and ΔPQR : ΔDEF ÞΔABC : transitive ΔDEF
So, the given relation is transitive, hence the relation is an equivalence
Equivalence Classes: An equivalence relation R on a set X divides X into mutually disjoint subsets Aᵢ, called partitions of X, satisfying:
- All elements of Aᵢ are related to each other.
- No element of Aᵢ is related to any element of Aⱼ for i ≠ j.
- The union of all Aᵢ covers the entire set X.
Aᵢ ∪ Aⱼ = X and Aᵢ ∩ Aⱼ = ∅, i ≠ j
Example: The rational numbers can be constructed as the set of equivalence classes of ordered pairs of integers (a, b) with b not zero, where the equivalence relation is defined by (a, b) R (c, d) if and only if ad = bc.
Here the equivalence class of the pair (a, b) can be identified with rational number a/b.
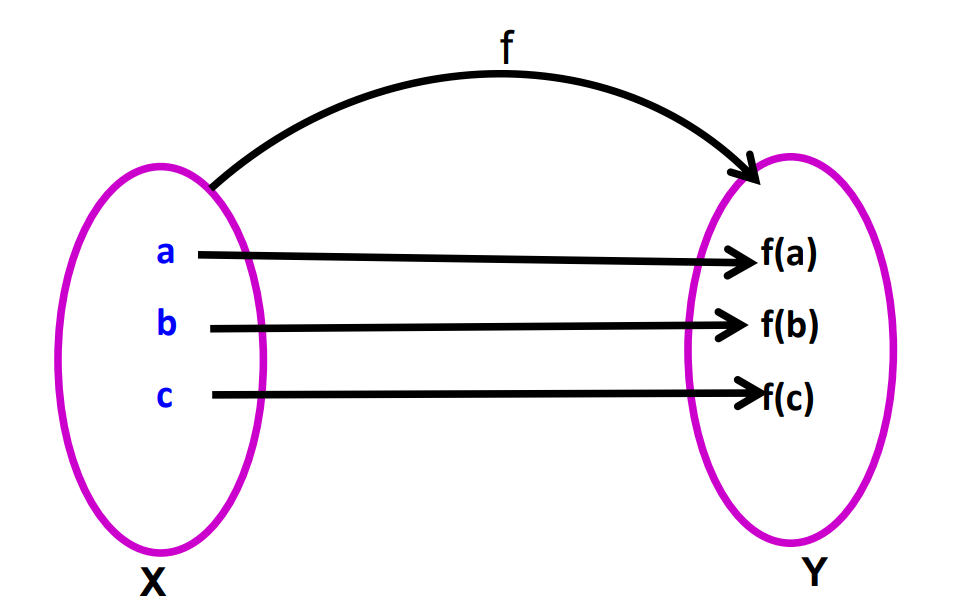
Functions: A function f from a set A to a set B is a rule that associates each element of A with a unique element of B.
All functions are relations, but not all relations are functions.
Example:
The function that associates a real number x to its square, i.e., x² is called the square function.
A function f: R → R defined by f(x) = x² is called the square function.
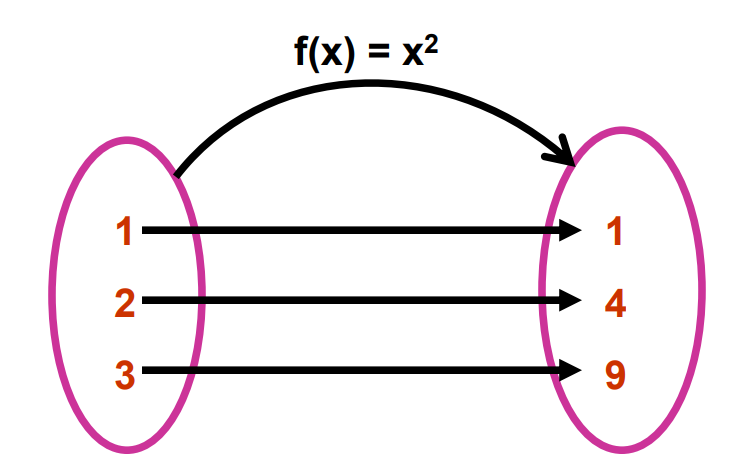
Types of Functions
- One-One (Injective) Function: A function f is one-one if distinct elements in the domain A map to distinct elements in the co-domain B.
For example, the function f:R→R defined by f(x)=x² is injective.
Arrow Diagram
Algorithm to check injectivity: Let f: A →B be the given function.
- Take two arbitrary elements a, b(say) in the domain of f.
- Put f(a) = f(b).
- Solve f(a) = f(b). If f(a) = f(b) gives a = b only, then f: A →B is an one – one (or injective) function, otherwise not.
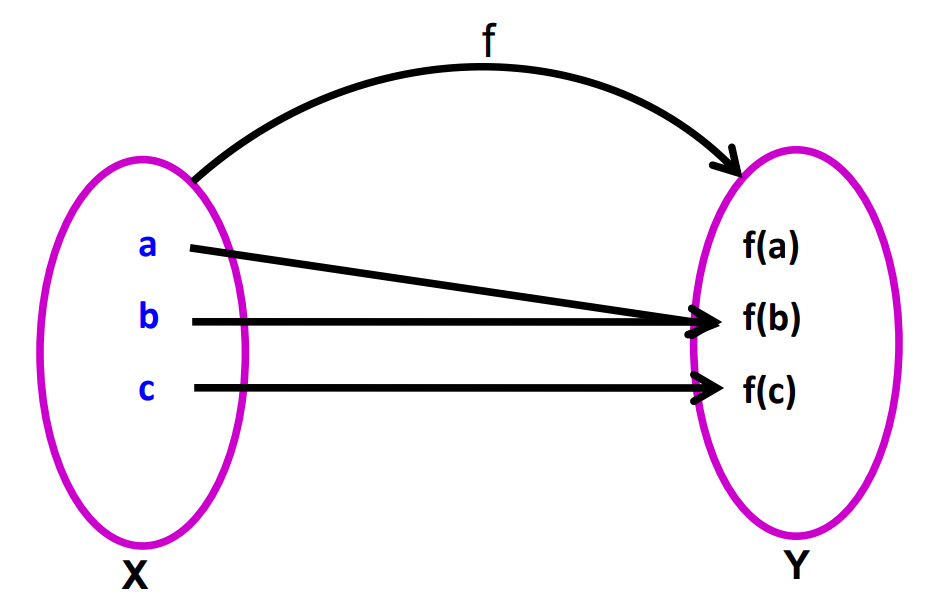
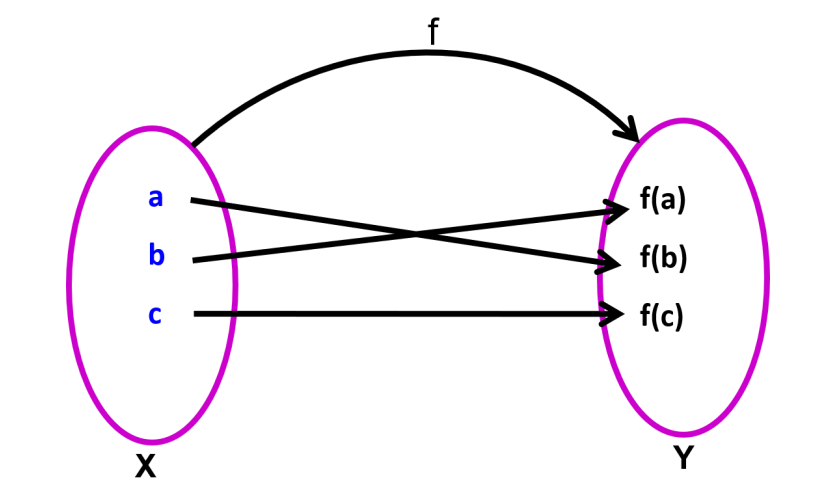
- Many-One Function: A function f is many-one if two or more elements of the domain have the same image in the co-domain.
For example, f(x) = x² is a many-one function because f(−1) = f(1).
Arrow Diagram:
- Onto (Surjective) Function: A function f is onto if every element of the co-domain B is the image of at least one element of the domain A.
For example, f:R→[−2,∞) given by f(x)=x² −2 is surjective.
Arrow Diagram
Algorithm to Check Surjectivity:
Let f: A →B be the given function.
- Choose an arbitrary element y in B.
- Put f(x) = y.
- Solve the equation f(x) = y for x and obtain x in terms of y.
- Let x = g(y).
- If for all values of y ∈ B the values of x obtained from x = g(y) are in A, then f is onto. If there are some y ∈ B for which x, given by x = g(y), is not in A, then f is not an onto function.
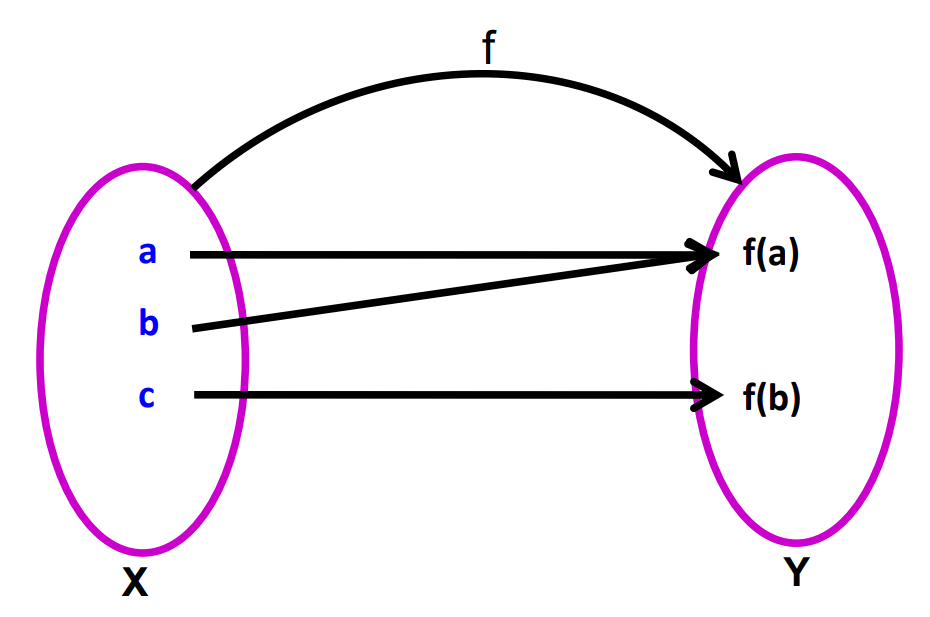
- Into Function: A function is into if there is at least one element in the co-domain B that is not the image of any element of the domain A.
The function f:N→N given by f(x)=2x is an into function because not all natural numbers f(N) = {2, 4, 6,…} ≠ N (codomain) are covered by the outputs.
Arrow Diagram:
A function f : X Y is said to be an into function if there exists an element in Y having no pre–image in X. In other words, f : X Y is an into function if it is not an onto function.
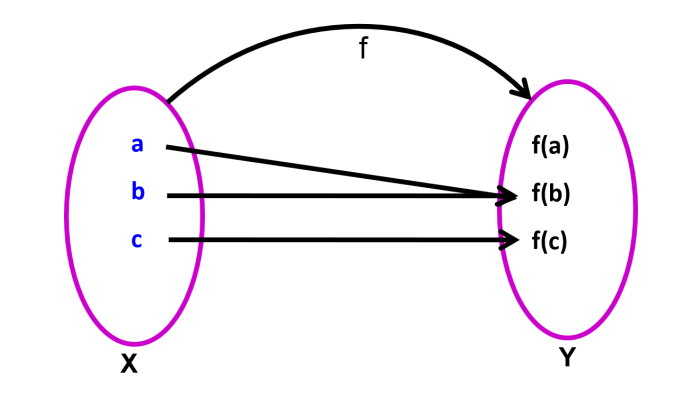
- Bijective Function (One-One Onto Function): A function is bijective if it is both one-one and onto.
For example, the function f:R→R defined by f(x)=2x is bijective.
Arrow Diagram:
A function f : X Y is said to be a one – one onto (bijection) function if it is one–one as well as onto.
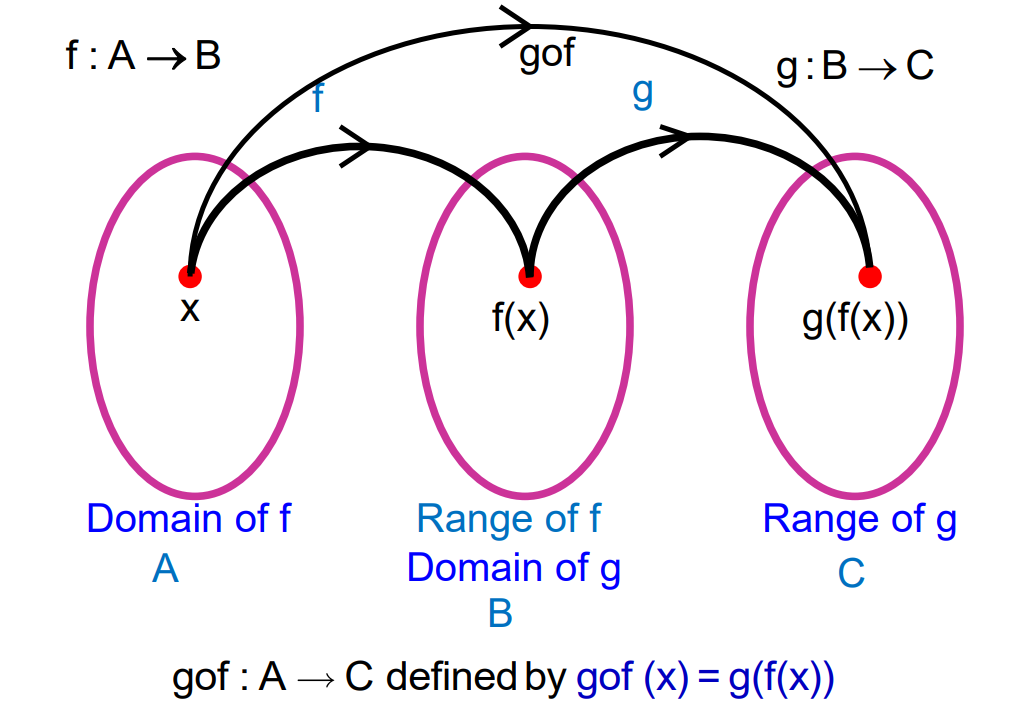
Composition of Functions: If f:A→B and g:B→C, then the composition of f and g is a function from A to C, denoted by gof, where (gof)(a) = g(f(a)) for all a∈A.
Example:
Given f(x) = 2x + 3 and g(x) = – x² + 5, find gof (x) and fog (x).
Let gof (x) = g(f(x)) = g(2x + 3) = –(2x + 3)² + 5 = –(4x² + 12x + 9) + 5 = –4x² – 12x – 9 + 5 = –4x² – 12x – 4
Now we need to find fog (x) = f (g(x)) = f (–x² + 5) = 2(–x² + 5) + 3 = –2x² + 10 + 3 = –2x² + 13
Invertible Functions: A function f: X→Y is invertible if there exists a function g:Y→X such that g∘f=Iₓ and f∘g=Iᵧ, where Iₓ and Iᵧ are identity functions on X and Y respectively. Only bijective functions are invertible.
For example, if f:R→R is given by f(x)=2x−3, its inverse is f⁻¹(y)= 2y+3
Example: Find f⁻¹of the function f : R→R given by f(x) = 2x – 3.
Consider an arbitrary element of y such that y = 2x – 3 for some x in domain R.
⇒ x = y +3 /2
Define g : R→R by g(y) = y +3 /2
Now gof(x) = g(f(x)= g(2x – 3) = 2x – 3 + 3 / 2 = x
and fog(y) = f(g(y)= f (y +3 /2) = 2(y +3 /2) – 3 = y
Thus, of = fog = Iᵣ
Hence, f is invertible and g is the inverse of f.
So, f⁻¹(x) = x + 3/2
Let’s Conclude
In conclusion, Relations and Functions is a fundamental chapter in CBSE Class 12th Mathematics that provides the foundation for understanding complex mathematical concepts. Mastering the different types of relations, functions, and their properties is essential for solving advanced problems in calculus and other areas. At iPrep, we are committed to making your learning experience smooth and engaging with our rich resources, including animated videos, practice exercises, and detailed notes. By grasping the key concepts in Relations and Functions, you’ll be well-equipped to excel in your studies and build a strong mathematical foundation. Dive into Relations and Functions with iPrep and enhance your learning journey!
Practice questions on Chapter 1 - Relations And Functions
Get your free Chapter 1 - Relations And Functions practice quiz of 20+ questions & detailed solutions
Practice Now








