Sets – Complete Guide For Class 11 Math Chapter 1

Our learning resources for Mathematics Class 11 ‘Sets’ Chapter 1 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.

Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Sets. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze. This chapter introduces the concept of sets, a fundamental idea in mathematics.

Introduction To Sets

A set is a well-defined collection of distinct objects or elements. The chapter covers various types of sets, including finite, infinite, equal, and empty sets. Key operations on sets, such as union, intersection, difference, and complement, are discussed, along with Venn diagrams for visual representation. It also explores subsets, power sets, and the concept of a universal set. Understanding these basic set operations and representations lays the foundation for advanced mathematical concepts in algebra, geometry, and calculus.

In a classroom setting, let’s define groups of students:

• Girl students of age group 15 to 17 years
• Students of Dance

These collections are well-defined and form sets.

On the other hand, consider the collection of Good Students. This is not well-defined, as the criteria for determining a “good student” can vary from person to person. Hence, this collection does not form a set.

Sets

Definition

A set is a well-defined collection of objects.

Examples:

1. The collection of rivers in India forms a set.
2. The collection of all prime numbers less than 30 forms a set.
3. The collection of all vowels in the English alphabet forms a set.
4. The collection of even natural numbers less than 8 forms a set.

Symbols: ∈ and ∉

• If an element belongs to a set, we use the Greek symbol ∈.
• If an element does not belong to a set, we use the symbol ∉.

Example:
If A is the set of all prime numbers, then
2 ∈ A, 3 ∈ A, but 4 ∉ A.

Representations of Sets

Methods of Representations

1. Roster or Tabular Form
2. Set-builder Form

1. Roster or Tabular Form

In this method, a set is represented by listing all the elements, separated by commas, and enclosed within braces {}.

Example: The set of all vowels in the English alphabet is represented in Roster form as

{a, e, i, o, u}.

Remarks:

1. Repetitions of elements are generally not allowed in roster form.
2. The order in which elements are listed is not important.

2. Set-builder Form

In this form, a set is described by stating a single common property of its elements.

Key Points:

1. A variable followed by a colon denotes each element of the set.
2. After the colon, the characteristic property is written.
3. The whole description is enclosed within braces.

Example:

{x: = p/q, where p and q are integers and q≠0}. This is the set of all rational numbers.

Empty Set

Definition

A set that does not contain any elements is called an empty set. It is also known as the null set or void set.

A null set is denoted by ϕ or {}.

Example:
The set of natural numbers less than 1 is empty.

Finite and Infinite Sets

Finite Set

A set that contains finite elements is called a finite set.

Example:
Let the set of boys be denoted by A.
A = {Raj, Ashu, Amit, Somveer, Dhanu, Sanju}

Infinite Set

A set that contains infinite elements is called an infinite set.

Example:
The set of multiples of 3 is represented by T.
T = {3,6,9,12,15,… }

Definition Recap

A set that is empty or contains finite elements is finite. Otherwise, it is an infinite set.

Examples:

1. The set {x:x ∈ Z and x² = 9} is finite because it contains only two elements: 3 and -3.
2. The set {x:x ∈ N and x is even} is infinite.

Equal Sets

Definition

Two sets A and B are equal if they have the same elements.

Example:
A = {x: x − 5 = 0}
B = {x : x ∈ N and x² = 25} 

Both sets are equal.

Subsets

Definition

A set A is a subset of set B if every element of A is also an element of B. This is symbolically represented as A ⊆ B.

If A is not a subset of B, we write A ⊈ B.

Intervals as Subsets of R

Let a < b and a, b ∈ R, then:

• (a,b) = {x: a < x < b} (open interval, excluding a and b)
• [a,b] = {x: a ≤ x ≤ b} (closed interval, including a and b)
• [a,b) = {x: a ≤ x < b}(including a but not b)
• (a,b] = {x: a < x ≤ b} (including b but not a)

The set (−∞,∞) describes the set of real numbers R, and all the intervals described above are subsets of R.

Power Set

Definition

For any set A, the power set is the collection of all subsets of A. It is denoted by P(A).

If the number of elements in A = m, then the number of subsets in the power set of A is 2ᵐ.

Example:
If A = {a,b}, then
P(A) = {∅,{a},{b},{a,b}}.

Universal Set

Definition

A universal set is the set of all objects or elements under consideration. It is denoted by U.

Example:
For the set of all integers, the universal set can be the set of all rational numbers.

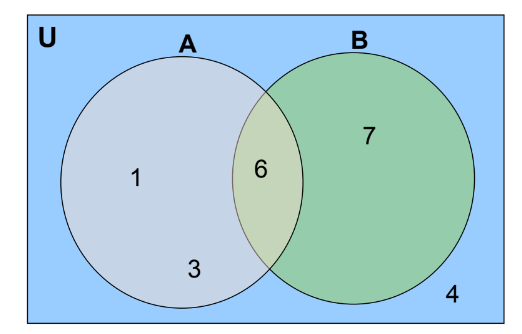
Venn Diagrams

A Venn diagram is a diagrammatic representation of sets. It typically consists of a rectangle (representing the universal set) and closed curves, usually circles, representing subsets within the universal set.

Example:
If A = {1,3,6}, B = {6,7} and U = {1,3,4,6,7}, the Venn diagram would look like this:

Operations on Sets

1. Union of Sets
2. Intersection of Sets
3. Difference of Sets
4. Complement of a Set

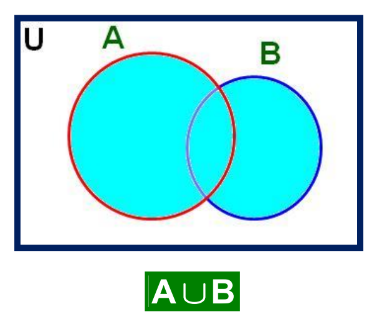
1. Union of Sets

The union of sets A and B is the set containing all elements of A and B, but common elements are taken only once. It is denoted by A∪B.

Example:
A∪B = {x: x ∈ A or x ∈ B}

2. Intersection of Sets

The intersection of sets A and B is the set of elements common to both sets. It is denoted by ABA.

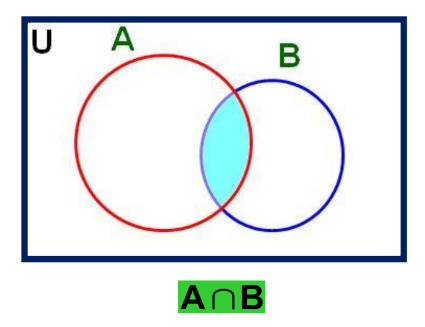
Example:
A∩B = {x: x ∈ A and x ∈ B}

Example:
If A = {1,3,5,7,9} and B = {2,4,5,6,8}, then:
(i) A∩B = {5}
(ii) A∪B = {1,2,3,4,5,6,7,8,9}

Properties of Union and Intersection

• Commutative Law:
  1. A∩B = B∩A
  2. A∪B = B∪A
• Associative Law:
  1. A∩(B∩C) = (A∩B)∩CA
  2. A∪(B∪C) = (A∪B)∪CA 
• Laws of ∅ and U:
  1. A∩∅ = ∅
  2. U∩A = A
  3. A∪∅ = A
  4. U∪A = U
• Idempotent Law:
  1. A∩A = A
  2. A∪A = A

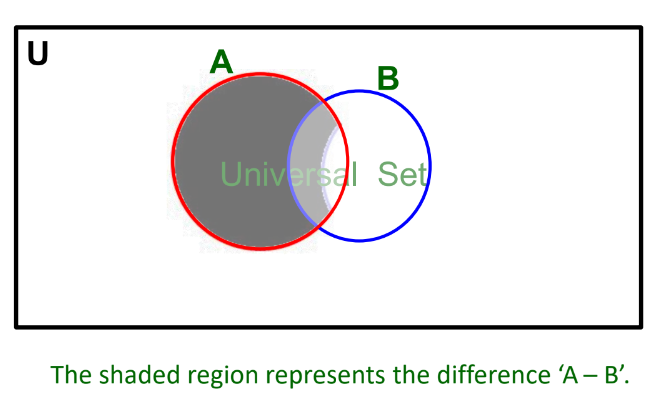
Difference of Sets

The difference between sets A and B written as “A – B” is the set of all the elements of A which do not belong to B.

Example

If A = {3, 6, 9, 12, 15, 18, 21, 24} and B = {6, 12, 18, 24, 30}, then

A – B = {3, 9, 15, 21}

Complement of a Set

If U is the universal set, then the complement of a set A is the set of all elements of U which are not the elements of A.

The complement of a set A is denoted by A’ or Aᶜ. Thus,

A’ = U – A = {x: x ∈ U and x ∉ A }

Properties of Complement Sets

1. Complement Law:
   • A∪A′ = U, where U is the universal set.
   • A∩A′ = ϕ, where ϕ is the empty set.
2. Law of Double Complementation:
   • (A′)′ = A, i.e., the complement of the complement of set A is the set A itself.
3. De Morgan’s Laws:
   • (A∪B)′ = A′∩B′
   • (A∩B)′ = A′∪B′
4. Complement of the Universal Set:
   • U′ = ϕ, i.e., the complement of the universal set is the empty set.
5. Complement of the Empty Set:
   • ϕ′ = U, i.e., the complement of the empty set is the universal set.

These properties are essential for simplifying set expressions and solving problems involving operations with sets.

Number of Elements in Sets

The number of elements in a set refers to the total count of distinct elements in a finite set. This is denoted by n(A), where A is a set.

Important Results on Number of Elements in Sets:

1. Union of Two Sets:

If A and B are two finite sets, then the number of elements in their union is given by:

n(A∪B) = n(A) + n(B) − n(A∩B)
This formula accounts for the common elements that are included in both sets.

2. Disjoint Sets:

If A and B are disjoint sets (i.e., A∩B = ϕ), then:

n(A∪B) = n(A) + n(B).

Let’s Conclude

In summary, our guide to CBSE Class 11 Math Chapter 1 – Sets provides a thorough exploration of this foundational topic. The chapter on Sets introduces students to crucial concepts, including definitions, types, and operations on sets, ensuring a solid understanding of both basic and advanced set theory. Through our comprehensive resources, such as engaging animated videos, interactive exercises, and detailed notes, mastering Sets becomes an enjoyable and enriching experience.

Our materials cover all essential aspects of the chapter, including the various methods for representing sets, the significance of subsets and power sets, and the practical application of Venn diagrams. With the integration of these learning tools, you are well-equipped to excel in understanding and applying the concepts of Sets in your mathematical studies. Embrace the journey of learning with confidence, knowing that our resources will support your mastery of Sets every step of the way.