Introduction to Three Dimensional Geometry – Complete Guide For Class 11 Math Chapter 11
Our learning resources for Mathematics Class 11 ‘Introduction to Three Dimensional Geometry’ chapter 11 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.
Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Introduction to Three Dimensional Geometry. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze.
What is Three Dimensional Geometry
Three Dimensional geometry studies shapes and objects in space that have length, width, and height. Chapter 11 introduces students to the fundamental concepts of Three Dimensional geometry, an essential topic in higher mathematics. It begins with the study of the coordinate system in 3D space, exploring points, lines, and planes through the use of coordinates (x, y, z). Students learn to compute the distance between two points, section formula, and direction cosines. The chapter also covers the equation of a line and plane in space, providing foundational tools for spatial understanding, essential for fields like physics, engineering, and architecture. These concepts extend 2D geometry into real-world applications.
- Let us locate the position of the point of contact of the ball lying on the floor of the room. We require perpendicular distances of the point from two adjacent walls of the room.

Another Example
- How will you locate the position of the central tip of the ceiling fan?
- We will not only require perpendicular distances of the point from two adjacent walls of the room but also the height of the point from the floor of the room.

Thus, three numbers representing perpendicular distances are required to locate the positions of points in space. Hence, we need Three Dimensional coordinate geometry.
Coordinate Planes and Axes
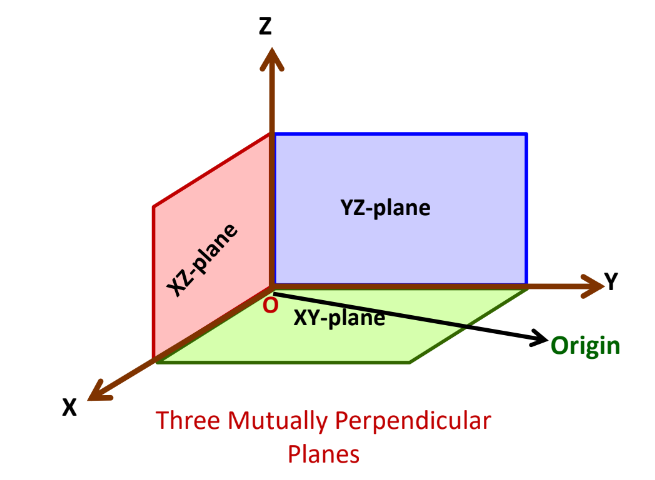
- These planes are called coordinate planes.
- The lines along which coordinate planes intersect are called coordinate axes.
Coordinate of a Point in Space
- The coordinates of a point in space are written in the form of the ordered triplet (x, y, z), where x, y, and z are the perpendicular distances of point P from the YZ, ZX, and XY planes.
- The three coordinate planes divide the space into eight parts, which are known as octants.
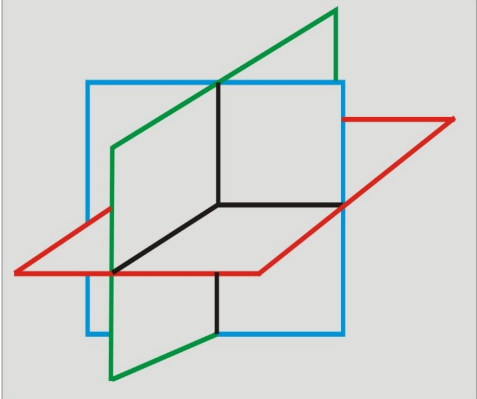
Sign of Coordinates in Different Octants
Octants OXYZ, OX’YZ, OX’Y’Z, OXY’Z, OXYZ’, OX’YZ’, OX’Y’Z’ and OXY’Z’ are denoted by I, II, III, IV, V, VI, VII and VIII respectively.
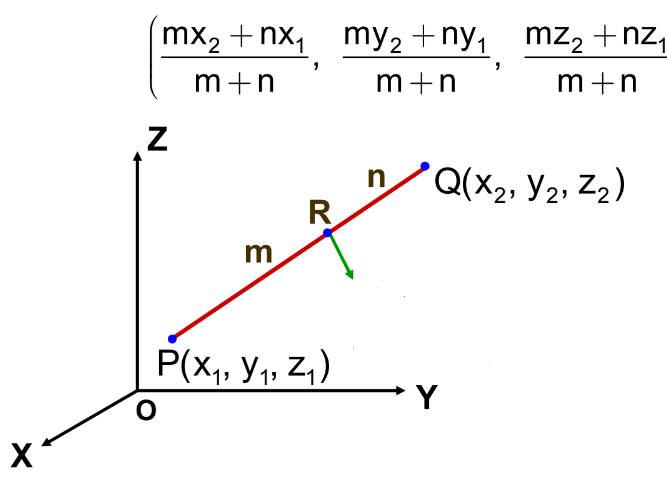
Coordinates of Any Point on Axes
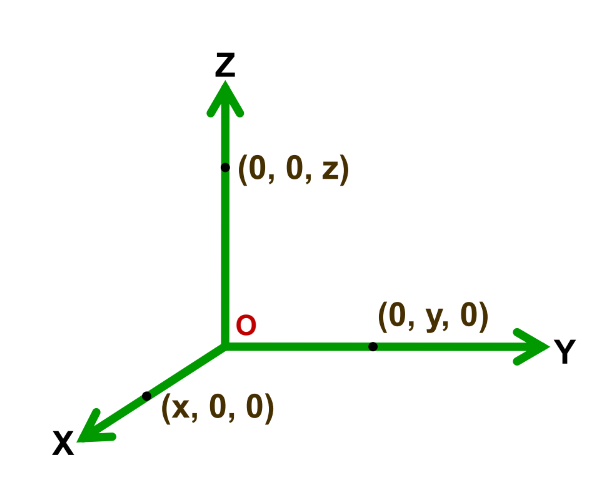
- The coordinates of any point on the x-axis are of the form (x, 0, 0).
- On the y-axis, the coordinates are (0, y, 0).
- On the z-axis, the coordinates are (0, 0, z).
Coordinates of Any Point on Coordinate Planes
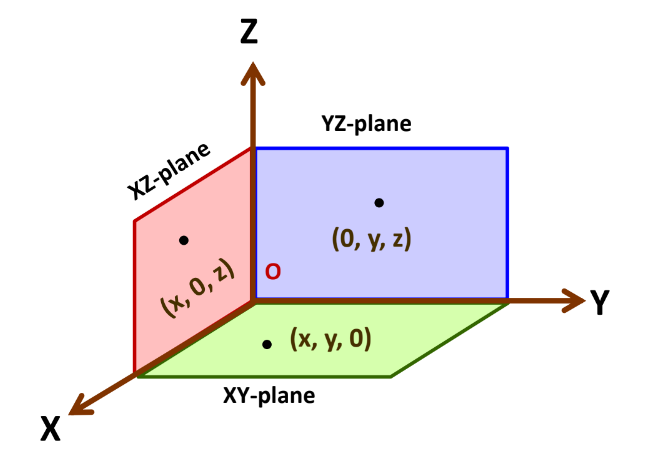
- For points on the XY-plane, the coordinates are (x, y, 0).
- On the YZ-plane, the coordinates are (0, y, z).
- On the XZ plane, the coordinates are (x, 0, z).
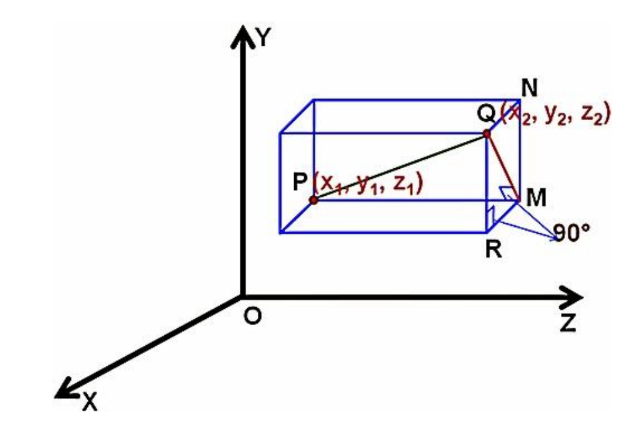
Distance Between Two Points
The distance between two points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is given by the formula:
PQ = √(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²
Example
Find the distance between the points A(-2, 4, 1) and B(1, 2, -5).
Solution:
AB = √(x₂ − x₁)² + (y₂ − y₁)² + (z₂ − z₁)²
AB = √(1 – (-1)² )+ (2 − 4)² + (-5 -1)² = √ 9 + 4 + 36 = √49 = 7 units.
Section Formula: Internal Division
Let P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be two points in space, and let R divide the line segment PQ internally in the ratio m: n. The coordinates of R are given by:
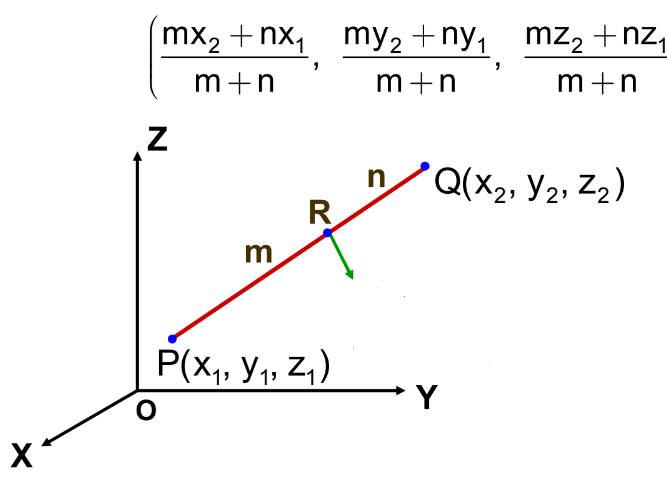
Section Formula: External Division
Let P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) be two points in space, and let R divide the line segment PQ externally in the ratio m: n. The coordinates of R are given by:
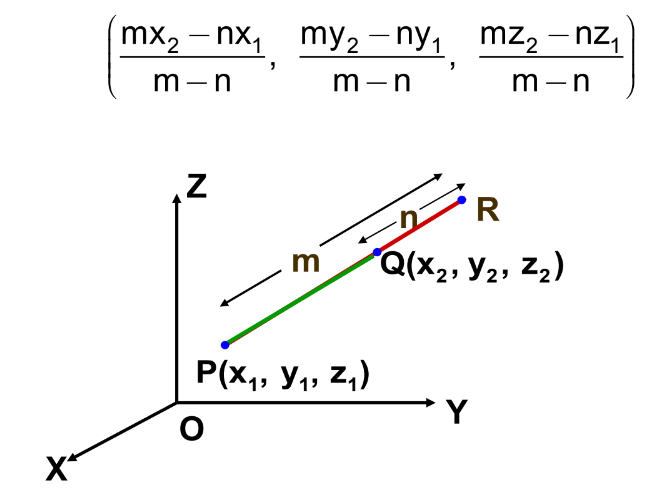
Example
Find the coordinates of the point that divides the line segment joining the points A(2, -1, 4) and B(4, 3, 2) externally in the ratio 2:3.
Solution: Let P(x, y, z) divide A and B externally. Using the section formula:
x = 2(4) – 3(2)/ 2 – 3, y = 2(3) – 3(-1)/2 – 3, z = 2(2) – 3(4)/2 – 3
x = -2, y = -9 and z =8
Thus, the required point is P(-2, -9, 8).
Coordinates of the Midpoint of a Line Segment
The midpoint M of the line segment joining points P(x₁, y₁, z₁) and Q(x₂, y₂, z₂) is:
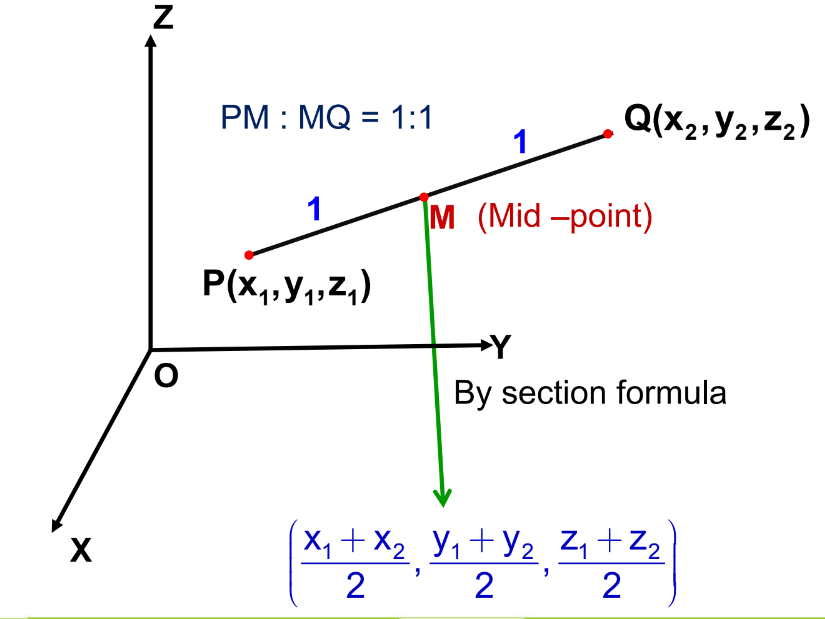
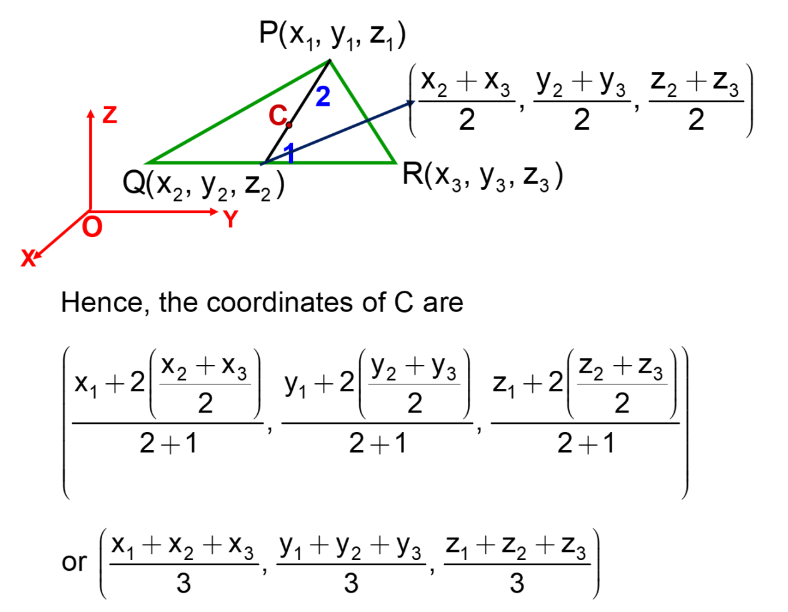
Coordinates of the Centroid of a Triangle
Let P(x₁, y₁, z₁), Q(x₂, y₂, z₂), and R(x₃, y₃, z₃) be the vertices of a triangle. The coordinates of the centroid C are:

This concludes Chapter 11 – Introduction to Three Dimensional Geometry. We have covered all the fundamental concepts and formulas related to Three Dimensional geometry. Understanding these principles is crucial for solving complex spatial problems in mathematics and related fields.
Let’s Conclude
In conclusion, the Introduction to Three Dimensional Geometry from CBSE Class 11 Math Chapter 11 serves as a foundation for understanding spatial relationships in mathematics. By mastering the concepts of coordinate planes, distance formulas, section formulas, and the various methods for dividing points in space, students can confidently approach more advanced topics. The chapter provides essential tools for fields like engineering, architecture, and physics, making it a crucial part of higher mathematics.
As you continue studying the Introduction to Three Dimensional Geometry, remember to practice applying these formulas to real-world problems for better retention and understanding. With the comprehensive resources available in our iPrep Learning Super App, including videos, notes, and interactive exercises, grasping the intricacies of Introduction to Three Dimensional Geometry will become an enjoyable and fulfilling experience.
Practice questions on Chapter 11 - Three Dimensional Geometry
Get your free Chapter 11 - Three Dimensional Geometry practice quiz of 20+ questions & detailed solutions
Practice Now








