Straight Lines – Complete Guide For Class 11 Math Chapter 9

Our learning resources for Mathematics Class 11 ‘Straight Lines’ chapter 9 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.

Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Straight Lines. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze.

Introduction To Straight Lines

In this chapter, we explore the fundamental concepts related to straight lines in coordinate geometry. Key topics include the slope of a line, various forms of the equation of a line (slope-intercept form, point-slope form, two-point form, and general form), and the concepts of parallel and perpendicular lines. The chapter also covers important geometric conditions such as the distance between two points, the distance of a point from a line, and the area of a triangle formed by three points. These concepts are essential for understanding higher-level geometry and calculus.

• In geometry, a line is a fundamental object, made up of points. Lines are an idealization of such objects, have no width or height, and are usually considered to be infinitely long.
• The Definition of a straight line: A line traced by a point traveling in a constant direction is called a straight line.
• In coordinate geometry, straight lines in a Cartesian plane are described algebraically by linear equations.

Slope of a Line

Let θ be the angle made by the line with the positive direction of the x-axis in an anticlockwise sense.
The slope of the line is defined as:

m = tan⁡θ

For θ = 90°, the slope is not defined.

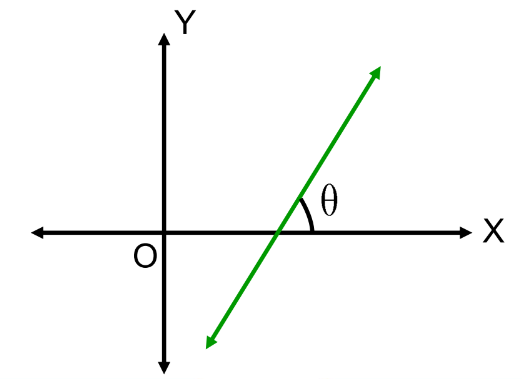
When Coordinates of Any Two Points on the Line are Given

Let A(x₁,y₁) and B(x₂,y₂) be two points on a non-vertical line L. The inclination of line L with the positive direction of the x-axis is θ. The slope of line L is given by:

m = tan⁡θ = y₂−y₁/x₂−x₁

​​

Example:

Find the slope of the line that passes through the points (1, 1) and (2, -2).

Solution:

m = −2−1/2−1 = −3

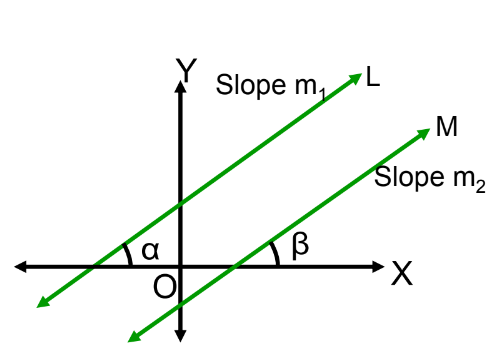
Condition for Parallelism of Lines in Terms of Their Slopes

Let L and M be two parallel lines with slopes m₁ and m₂, respectively. Let α and β be their inclinations with a positive direction of the x-axis. 

If two lines are parallel then their inclinations with the positive direction of the x-axis are equal.

α = β

Therefore tan α =tan β

m₁ = m₂

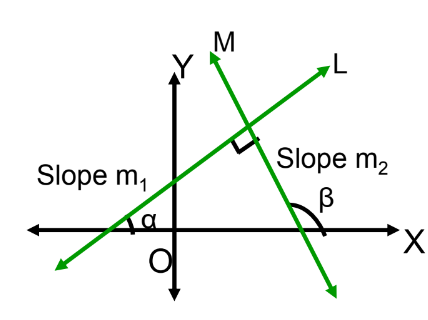
Condition for Perpendicularity of Lines in Terms of Their Slopes

Let L and M be two perpendicular lines with slopes m₁ and m₂​. If their inclinations with the positive direction of the x-axis are θ and θ + 90°, then:

m₁ . m₂ = −1

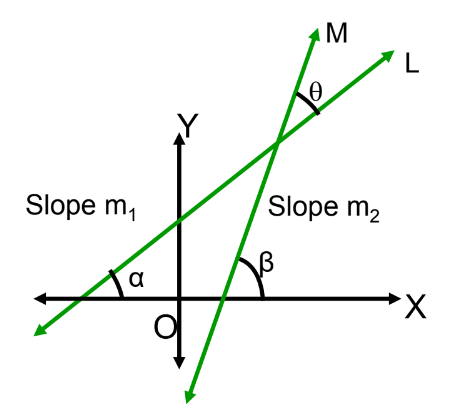
Angle Between Two Lines

Let L and M be two non-vertical lines with slopes m₁ and m₂​ respectively. Let α and β are their inclinations with the positive direction of the x-axis, then θ = β – α and α,β ≠ 0.

Therefore tan θ = tan β – tan α / 1 + tan β. tan α  = m₂ – m₁ / 1+ m₁m₂

If m₂ – m₁ / 1+ m₁m₂ is positive, θ will be acute and 

If m₂ – m₁ / 1+ m₁m₂ is negative, θ will be obtuse.

Also ∅ = 180 – θ

tan ∅ = – (m₂ – m₁ / 1+ m₁m₂)

If m₂ – m₁ / 1+ m₁m₂ is positive, ∅ will be acute and 

If m₂ – m₁ / 1+ m₁m₂ is negative, ∅ will be obtuse.

Thus, the acute angle between the two lines with slopes m₁ and m₂ is tan θ = ∣ m₂ – m₁ / 1+ m₁m₂ ∣ 

Example:

The slopes of the two lines are 1/2​ and 3/2​. Find the angle between them.

Solution:

Collinearity of Three Points

Three points P, Q, and R are collinear if:

slope of PQ = slope of QR

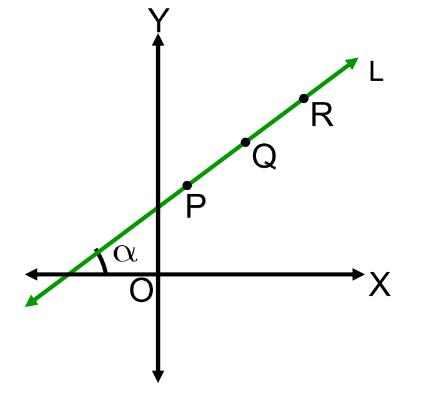
Example:

Are the points P(5,2), Q(3,−1) and R(7,3) collinear?

Solution:

• Slope of PQ = −1−2/3−5 = −3/−2 = 3/2
• Slope of QR = 3−(−1)7−3 = 4/4 = 1

Since the slopes are not equal, the points are not collinear.

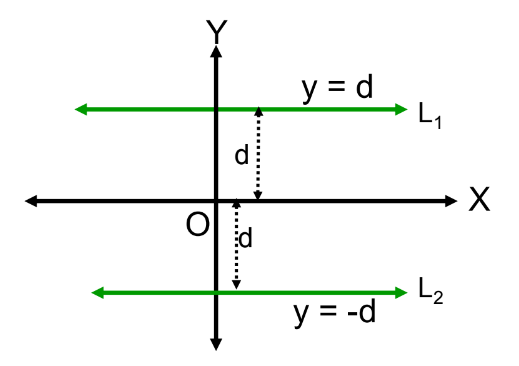
Equation of a Line Parallel to X-axis

• A line parallel to the x-axis at a distance d above the x-axis has the equation:
  y = d.
• A line parallel to the x-axis at a distance d below the x-axis has the equation:
  y = −d.

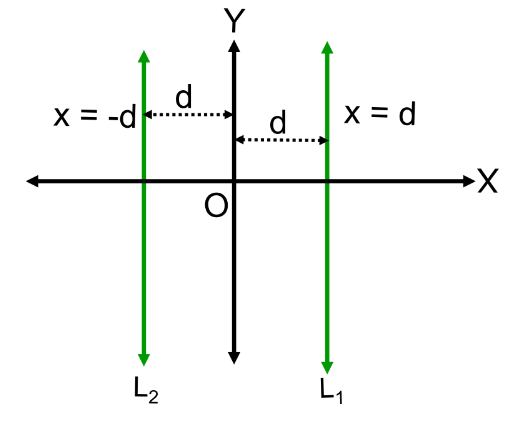
Equation of a Line Parallel to Y-axis

• A line parallel to the y-axis at a distance d to the right of the y-axis has the equation:
  x = d.
• A line parallel to the y-axis at a distance d to the left of the y-axis has the equation:
  x = −d.

Various Forms of Line Equations in Straight Lines

Within the chapter Straight Lines from class 11 math, there are various forms of line equations in straight lines. Those include- 

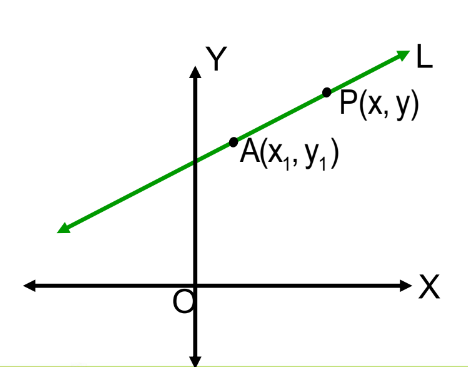
Point-Slope Form

If a line passes through a fixed point A(x₁,y₁), the equation of the line is:

y − y₁ = m (x−x₁)

Example:

The perpendicular from the origin to the line y = mx+c meets it at (−1,2). Find m and c.

Solution: 

From y = mx+c, substituting the point (−1,2):

−1⋅m+c = 2

-m + c = 2

Using the points (0, 0) and (-1, 2), we get the slope of the perpendicular line.

Since the lines are perpendicular, we get m = 1⁄2.

Substituting the value of m in the first step, we get c.

Two-Point Form

If a line passes through two points A(x₁,y₁) and B(x₂,y₂), the equation is:

y – y₁ = y₂ – y₁/  x₂ – x₁ .(x – x₁)

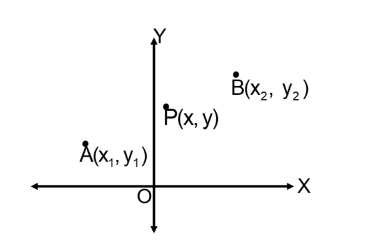
Slope-Intercept Form

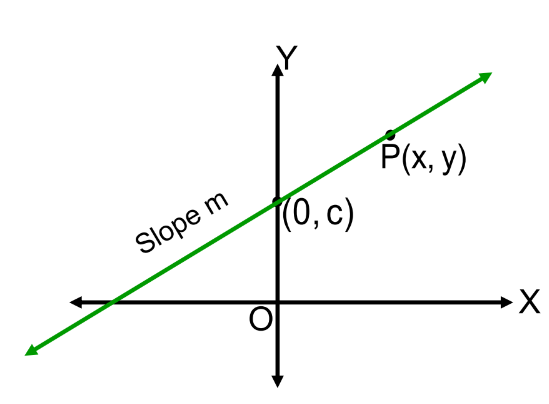
The equation of a line with slope m and y-intercept c is:

y = mx + c

Intercept Form

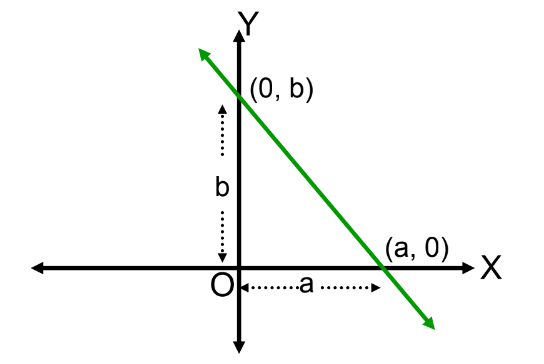
The equation of a line making intercepts a and b on the x-axis and y-axis is:

x/a + y/b=  1

Normal Form

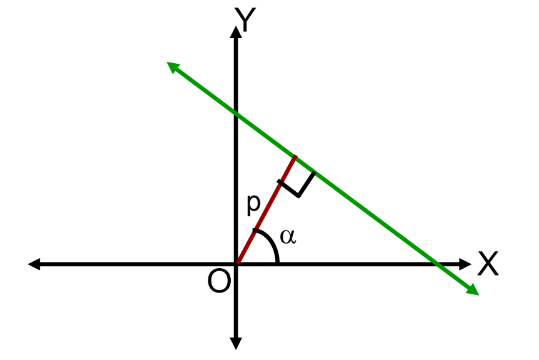
The equation of a line having a normal distance p from the origin and angle α is:

x cos⁡ α + y sin ⁡α = p

General Equation of a Line

The equation of a line in general form is:

Ax + By + C = 0

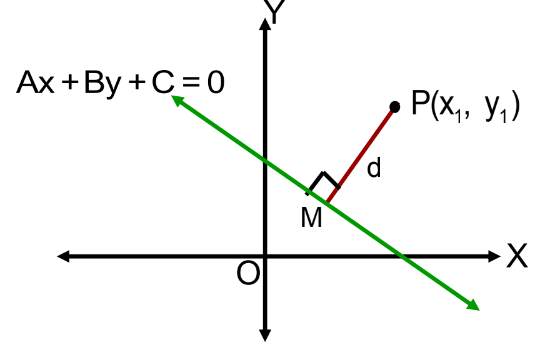
Distance of a Point from a Line

The distance of a point P(x₁,y₁) from a line Ax + By + C = 0 is:

d = ∣Ax₁+By₁+C∣/√A²+B²

Example:

Find the distance between the line 2x − y + 1 = 0 and the point (1,−1).

Solution:

d = ∣Ax₁+By₁+C∣/√A²+B²

d = ∣2(1)−(−1)+1∣√2²+(−1)² = 4/√5

Distance Between Two Parallel Lines

For parallel lines y = mx+c₁ and y = mx+c₂​, the distance between them is:

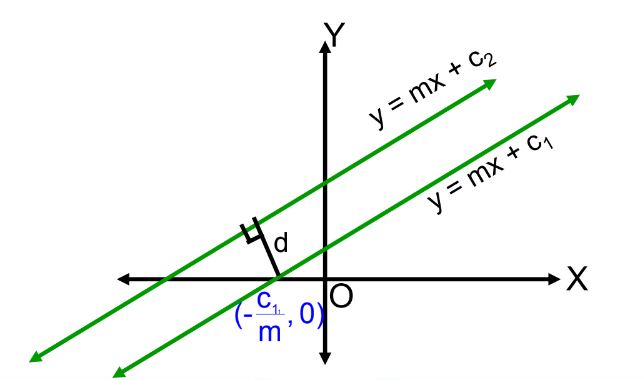
d = ∣c₁ − c₂∣/√1+m²​

For lines in general form Ax + By + C₁ = 0 and Ax + By + C₂​=0:

d = ∣C₁ − C₂∣/√A²+B²

Let’s Conclude

In conclusion, the CBSE Chapter 9 of Class 11 Math, Straight Lines, provides a foundational understanding of key concepts in coordinate geometry. By mastering the equations of straight lines, including the slope-intercept, point-slope, and general forms, you will gain valuable skills applicable to higher mathematics. Our resources ensure that your journey through Straight Lines is engaging and effective, empowering you to tackle problems with confidence. Remember, a solid grasp of this chapter will not only help you excel in exams but also pave the way for more advanced topics in geometry and calculus. Embrace the challenge and enjoy the learning experience as you navigate through Straight Lines!