Sequences and Series – Complete Guide For Class 11 Math Chapter 8
Our learning resources for Mathematics Class 11 ‘Sequences and Series’ chapter 8 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.
Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Sequences and Series. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze.
Introduction To Sequences and Series
Sequences and Series in Class 11 Mathematics introduces the study of ordered lists of numbers called sequences and their associated sums called series. A sequence is a set of numbers arranged in a specific order, and a series is the sum of terms of a sequence. This chapter covers arithmetic progression (AP), geometric progression (GP), and other important types of sequences. It explores formulas for the n-th term and the sum of terms for both AP and GP. The chapter also introduces special series like the sum of squares and cubes of the first n natural numbers.
In this chapter, we explore the concept of sequences and series, including their types, properties, and applications. The focus is on arithmetic and geometric progressions (A.P. and G.P.), their general terms, sum formulas, and key concepts like arithmetic and geometric means.
Let us observe the number of squares in the following pattern:
The observed numerical pattern is 1, 4, 9, 16, …
Also, let us observe the lengths of the rungs of a ladder:
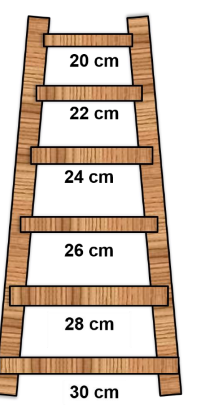
30, 28, 26, 24, 22, 20, …
These patterns are generally known as sequences.
Sequence
- A sequence is an arrangement of numbers in a definite order according to some rule.
- In other words, a sequence can be defined as a function whose domain is the set of natural numbers.
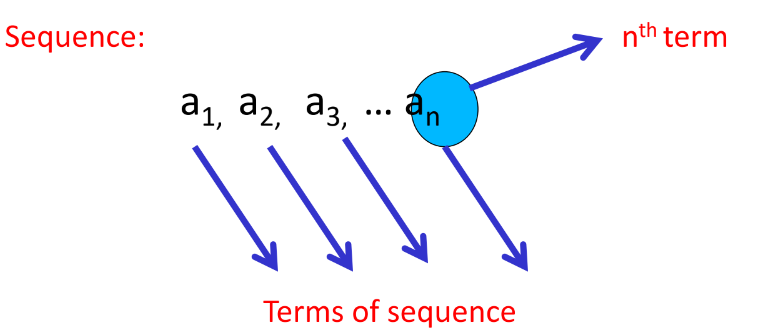
Terms of a Sequence
A sequence is denoted by: the nth term: a₁, a₂, a₃, … aₙ
These are known as the terms of the sequence.
Finite Sequence
- A sequence containing a finite number of terms is called a finite sequence.
- For example, the sequence of even natural numbers between 1 and 100 is: 2, 4, 6, …, 100
Infinite Sequence
- A sequence is called infinite if it is not finite.
- For example, the sequence of odd natural numbers is 1, 3, 5, …
Series
If a sequence is: a₁, a₂, a₃, … aₙ,
Then a series is: a₁ + a₂ + a₃ + … + aₙ
A series is an expression consisting of the terms of a sequence with the symbol ‘+’.
Progression
A sequence is said to be a progression if it follows a certain pattern.
Let us observe the number of fish in each column:

The observed sequence is 2, 4, 6, 8…, We find that each number, other than the first number, is obtained by adding a fixed number 2 to the immediate preceding number.
Such a number pattern is said to form an arithmetic progression (A.P.)
Arithmetic Progression (A.P.)
A sequence is called an arithmetic progression (A.P.) if each term, except the first, is obtained by adding a fixed number to the immediately preceding term.
For example:
a₁, a₂, a₃, … aₙ
In an A.P.:
a₂ = a₁ + d, a₃ = a₂ + d, …, aₙ = aₙ₋₁ + d
This fixed number (d) is called the common difference.
Thus, a₂ – a₁ = a₃ – a₂ = … = aₙ – aₙ₋₁ = d.
General Term of an A.P.
Consider an arithmetic progression a, a + d, a + 2d,… with first term a and common difference d.
The general term is given by:
Nth term aₙ = a + (n – 1)d
Example: Show that the sequence 4, 9, 14, 19, … is an A.P. Find its 16th term and the general term.
Solution:
We have, 9 – 4 = 14 – 9 = 19 – 14 = 5.
Therefore, the given sequence is an A.P. with a common difference of 5 and first term 4.
The 16th term:
a₁₆ = 4 + 15 × 5 = 79
General term:
aₙ = 4 + (n – 1) × 5 = 5n – 1
Arithmetic Mean (A.M.)
For two numbers a and b, the arithmetic mean (A.M.) is given by:
A = a+b/2
A is called the arithmetic mean of a and b.
Geometric Progression (G.P.)
A sequence is called a geometric progression (G.P.) if the ratio of each term (except the first one) to its preceding term is constant. This constant ratio is called the common ratio (r).
For example, the sequence 1, 2, 4, 8 is a G.P. with the first term a = 1 and common ratio r = 2.
General Term of a G.P.
The general term of a G.P. is given by:
The Nth term of a GP is given by –
aₙ = arⁿ⁻¹

Sum to First n Terms of a G.P.
The sum of the first n terms of a G.P. is given by:
Sₙ = a(rⁿ – 1/r – 1) or Sₙ = a(1-rⁿ /1 – r) , for r ≠ 1
Sum to Infinite Terms of a G.P.
For a G.P. with an infinite number of terms, the sum is:
S∞ = a/1 − r, if ∣r∣<1
Geometric Mean (G.M.)
Let a and b be two positive numbers.
Insert a number G such that a, G, b is a G. P.
So, G/a = b/G
G² = √ab
Relationship Between A.M. and G.M.
For two positive numbers a and b, let A be the arithmetic mean and G be the geometric mean. Then:
A≥G
Special Series
The sum of the first n natural numbers is:
n(n+1)/2
The sum of the squares of the first n natural numbers is:
n(n+1)(2n+1)/6
The sum of the cubes of the first n natural numbers is:
{n(n+1)/2}²
Let’s Conclude
In conclusion, mastering Sequences and Series from CBSE Class 11 Math Chapter 8 is crucial for building a strong foundation in advanced mathematical concepts. Through a blend of arithmetic and geometric progressions, this chapter equips you with essential tools for solving real-world problems. With our comprehensive resources, including animated videos, practice exercises, and detailed notes, you can confidently tackle every topic covered in Sequences and Series Class 11 Math Chapter 8. Stay consistent with your learning, and you’ll find that Sequences and Series Class 11 Math Chapter 8 becomes much easier to navigate and understand. Happy learning!
Practice questions on Chapter 8 - Sequences and Series
Get your free Chapter 8 - Sequences and Series practice quiz of 20+ questions & detailed solutions
Practice Now








