Permutations And Combinations – Complete Guide For Class 11 Math Chapter 6
Welcome to iPrep, your go-to destination for all your learning needs. Our learning resources for Mathematics Class 11 ‘Permutations and Combinations’ chapter 6 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.
Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Permutations and Combinations. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze.
Introduction to Permutations and Combinations
Permutations and Combinations, a crucial topic in Class 11 Mathematics, explores methods of counting and arranging objects. Permutations refer to the different ways objects can be arranged in a specific order, while combinations focus on selecting objects without regard to order. This chapter covers key concepts like factorial notation, the fundamental principle of counting, the difference between permutations with or without repetition, and binomial coefficients. By the end of the chapter, students will be able to solve complex problems related to arranging and selecting objects in various contexts.
In this chapter, we will explore the fundamental techniques used to count the number of ways objects can be arranged or selected. These methods will help solve problems related to permutations and combinations without needing to list out all possibilities.
Consider a scenario where you need to choose a bat and a ball.
There are 3 different bats and 3 different balls.
The total number of possible selections is 9 ways.

However, for larger numbers of objects, listing all possible selections would be tedious. Fortunately, there are basic techniques that allow us to efficiently calculate the number of ways to arrange and select objects without having to list them all.

This chapter will cover the Fundamental Counting Principle, which will help us count how many ways a task can be performed when a series of events are involved.
Fundamental Principle of Counting
Let’s understand the principle through an example:
- Suppose an event can occur in 3 ways.
- After this event, another event can occur in 2 ways.
We can observe all possible ways for these events to occur together:
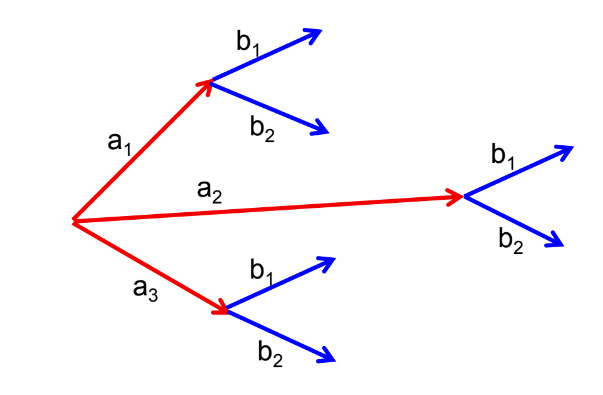
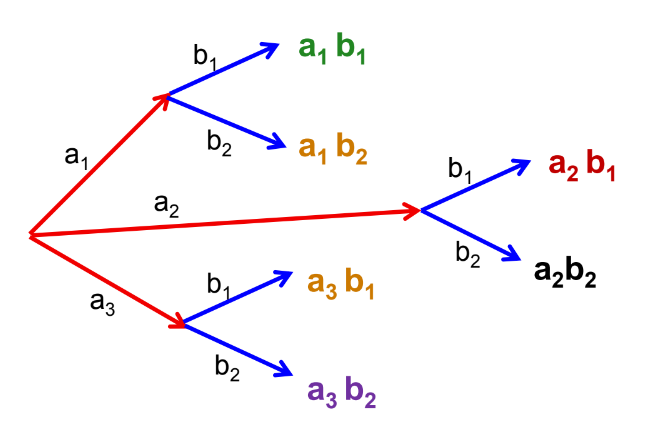
Thus, the number of possible ways these events can occur is 3 × 2 = 6.
Multiplication Principle
- If event A can occur in exactly m ways, and following it, event B can occur in exactly n ways, then the two events A and B can occur in exactly m × n ways.
This principle can also be generalized for any finite number of events.
Example:
Sonali is taking a test with four True/False questions. Each question has two possible answers. How many ways can she answer the entire test?
- There are four questions, and each has two possible answers:
Therefore, the required number of ways is 2×2×2×2=16.
Addition Principle
Let’s say a person wants to take either a red flower or a white flower.
If there are 6 red flowers and 5 white flowers, the total number of ways to take a flower is 6 + 5 = 11 ways.
If there are two mutually exclusive events, such that they can occur independently in m and n ways, respectively, then either of the two events can occur in m + n ways.
Example:
If we draw one card from a standard deck of playing cards, there are 4 ways of choosing a king and 4 ways of choosing a queen. Since we cannot choose both a king and a queen in one draw, the total number of ways of getting a king or a queen is 4 + 4 = 8 ways.
Factorial Notation
The notation n! represents the product of the first n natural numbers.
- We read this symbol as n factorial.
- 1×2×3×…×(n−1)×n = n!
- We define 0! = 1.
- Factorials of fractions or negative integers are not defined.
Permutations
A permutation is an arrangement in a definite order of several objects taken some or all at a time.
When all the objects are distinct and repetition is not allowed, the number of permutations of n different objects taken r at a time is given by the formula:
ⁿPᵣ = n!/(n−r)!
Example:
The number of permutations of 6 boys out of 8 boys to stand in a queue is:
P(8,6) = 8!/(8−6)! = 8×7×6!/6! = 8×7 = 56
When repetition is allowed, the number of permutations of n different objects, taken r at a time, is nʳ.
Example:
The number of three-digit numbers made using the digits 4, 6, and 8, where repetition is allowed, is:
3×3×3 = 27
Combinations
A combination is a selection made by taking some or all of several objects, regardless of their arrangement.
The number of all combinations of n distinct objects, taken r at a time, is denoted by ⁿCᵣ and is given by the formula:
ⁿCᵣ = n!/r!(n−r)!, where 0 ≤ r ≤ n.
Example:
The number of combinations of 2 fruits out of 4 fruits is:
C(4,2) = 4!/2!(4−2)! = 4/2!2! = 4×3×2!/2×2! = 6
Properties of Permutations and Combinations
- ⁿCᵣ = ⁿCₙ₋ᵣ, where 0 ≤ r ≤ n.
- ⁿCᵣ + ⁿCᵣ₋₁ = ⁿ⁺¹Cᵣ, where 0 ≤ r ≤ n.
- ⁿCₓ = ⁿCᵧ, x = y or x + y = n
- ⁿPᵣ = ⁿCᵣ×r!, 0 < r ≤ n
- ⁿC₀ = ⁿCₙ = 1
- ⁿPₙ = ⁿPₙ₋₁
Let’s Conclude
In conclusion, Chapter 6 of NCERT Class 11 Mathematics, Permutations and Combinations, comprehensively explores counting and arrangement techniques. Understanding the principles of permutations and combinations is crucial for solving various problems related to arranging and selecting objects. This chapter covers everything from basic factorial notation to advanced concepts like permutations with repetition and combinations, ensuring a solid grasp of these foundational topics.
By mastering Permutations and Combinations, students can approach complex mathematical problems with confidence. The detailed explanations and examples in this chapter will aid your current studies and lay a strong foundation for future mathematical concepts. Dive into this chapter with enthusiasm and utilize the resources provided to enhance your understanding and excel in your exams. With iPrep’s engaging content and thorough coverage of Permutations and Combinations, you’re well on your way to mastering this essential topic.
Practice questions on Chapter 6 - Permutations and Combinations
Get your free Chapter 6 - Permutations and Combinations practice quiz of 20+ questions & detailed solutions
Practice Now








