Electric Charges and Fields – Complete Guide For Class 12 Physics Chapter 1
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Electric Charges and Fields in Physics for Class 12th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.
The chapter Electric Charges and Fields introduces the fundamental concepts of electrostatics. It covers the nature of electric charges, the interactions between like and unlike charges, and the methods of charging objects. The chapter Electric Charges and Fields, explains Coulomb’s Law, which describes the force between two point charges and introduces the concept of the electric field as the region around a charge where other charges experience a force. Fundamental principles such as the additivity, quantization, and conservation of charge are also highlighted. Finally, the concept of the electric field is defined as the region around a charge where other charges experience a force, emphasizing its vector nature and the relationship with Coulomb’s force.
Electric Charges and Fields
Electric charges are the source of one of the most familiar yet powerful forces in nature. A common manifestation of this force is observed during a thunderstorm as lightning, where massive electric charges are discharged.

Origin and Definition
As stated in the chapter Electric Charges and Fields, the term electricity is derived from the Greek word ‘Elektron’, which means amber. Amber, a petrified tree resin, when rubbed with silk, attracts light objects such as small bits of paper or dust. This phenomenon reveals the presence of electric charges, indicating that the body has been electrified or charged.
Electric Charges
There are several facts about the electric charges mentioned in Electric Charges and Fields Class 12 Physics Chapter 1. These include-
- An object becomes positively charged by losing electrons.
- An object becomes negatively charged by gaining electrons.
- Objects without any net charge (neither positive nor negative) are considered neutral.
Types of Charges
Electric charge is a fundamental physical quantity responsible for electric and related effects in matter. As mentioned in class 12 physics chapter 1 – Electric Charges and Fields, it comes in two types:
- Positive Charge 2. Negative Charge

- Like charges repel each other
- Unlike charges attract each other
Electroscope

An electroscope is a simple device used to detect and measure small magnitudes of electric charge. It typically consists of a metal rod, metal plate, insulator, and gold foil leaf. When a charged object is brought near the electroscope, the gold leaves deflect, indicating the presence of a charge.
Construction and Working
Further in the chapter Electric Charges and Fields comes the topic of construction and working. This involves-
- Components: Metal rod, metal plate, insulator, gold foil leaf.
- Detection: When a charged object is near the electroscope, the gold leaves deflect, revealing the presence and magnitude of the charge.
Conductors and Insulators
- Conductors

Conductors are materials that contain free electric charges (electrons), allowing electricity to pass through them.
Examples: Iron nails and metals.
- Insulators

Insulators lack free electric charges and do not allow electricity to pass through them.
Examples: Wood and plastics.
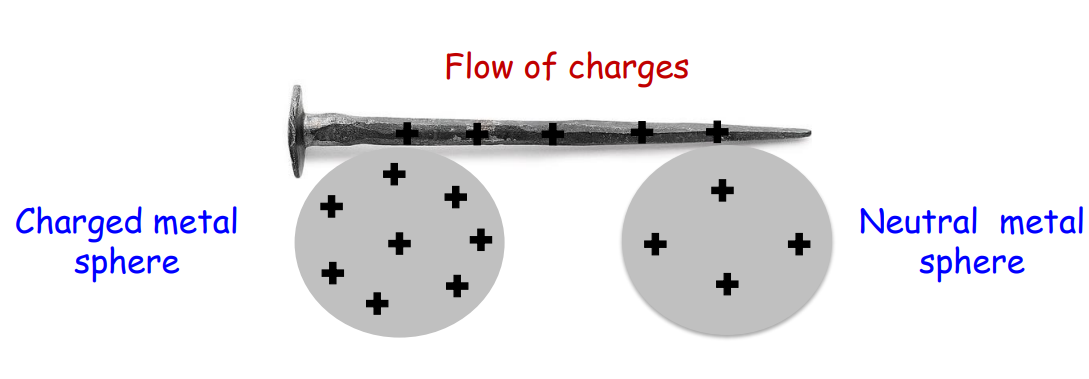
Charging by Induction
Charging by induction as stated in the chapter Electric Charges and Fields, involves charging an object without direct contact.
Here’s how it works:
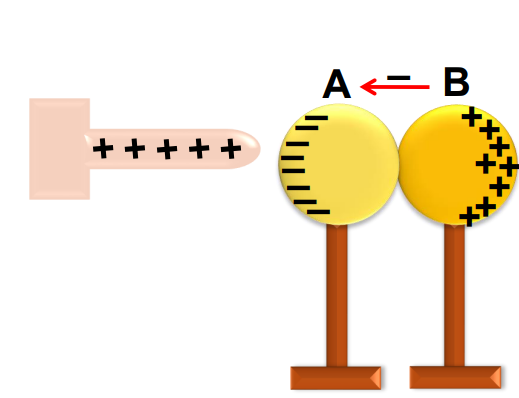
Initial Setup: Consider two uncharged metal spheres, A and B, in contact and mounted on insulated stands.
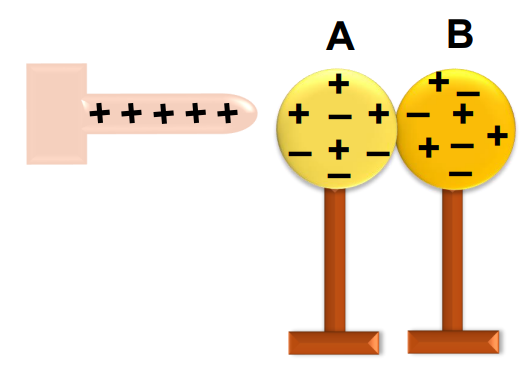
Inducing Charge: Bringing a positively charged rod near the spheres attracts electrons towards sphere A, leaving sphere B positively charged.
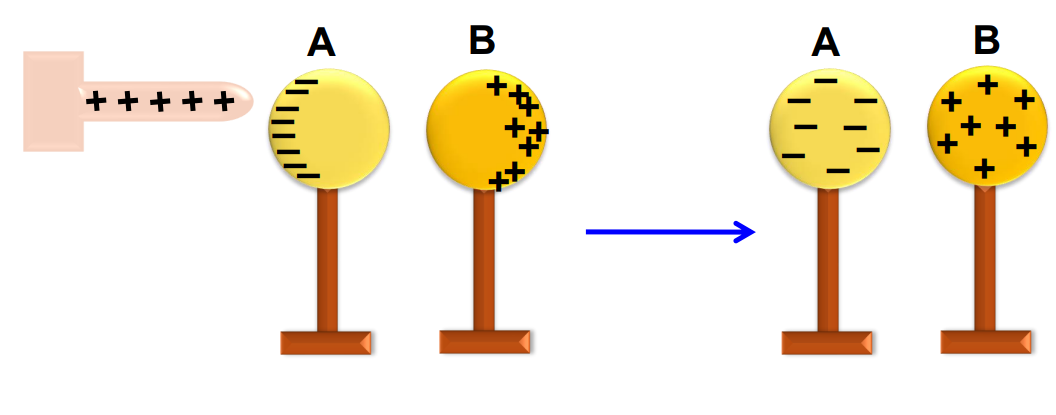
Separation and Distribution: Separating the spheres while the rod is present and then removing the rod distributes the charge evenly across both spheres.
Use of Grounding in Induction Charging
Grounding helps in induction charging by providing a path for excess electrons to flow into the earth, leaving the object with a net positive charge, as stated in the chapter Electric Charges and Fields.
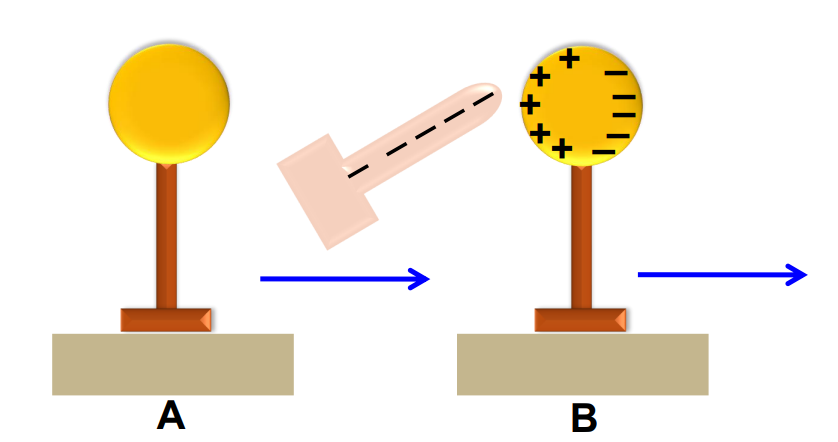
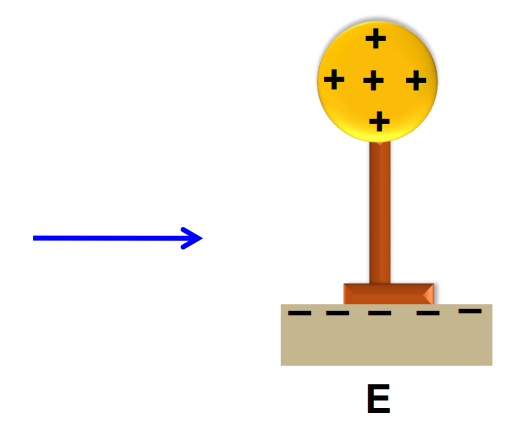
Let us consider an uncharged metal sphere supported by an insulated stand (figure A).
- A negatively charged rod is brought near it (figure B). The excess electrons on the rod repel the free electrons in the metal sphere away from the rod. At the same time, they attract positive charges towards the rod.
- These cannot escape from the sphere as the stand and the air surrounding it are insulators. This end is grounded with the earth by a wire through which the free electrons flow into the earth (figure C).
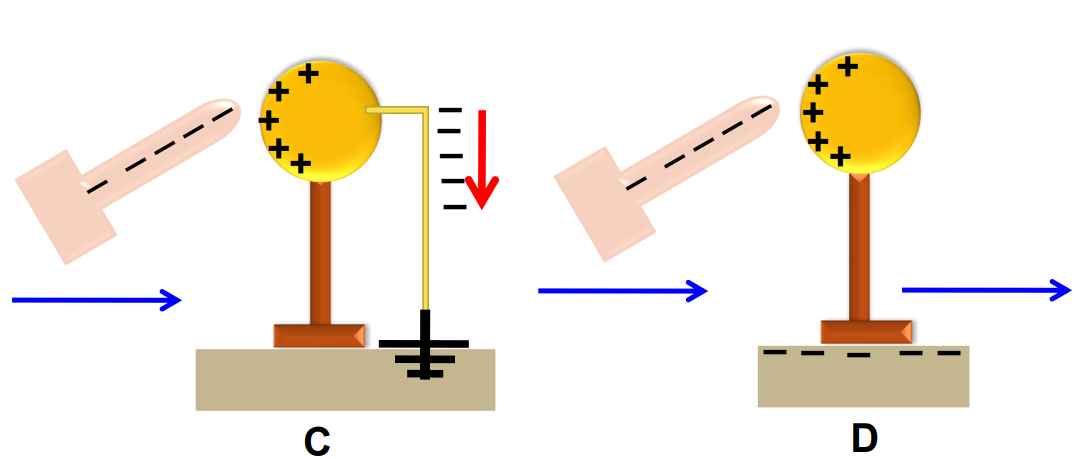
- Then, the charged rod is removed and the positive charges get distributed evenly on the whole sphere (figure E).
Additivity of Charge
The total charge of a system is the algebraic sum of all charges within it.
For example, if a system has charges q₁, q₂, q₃, ……, qₙ. The total charge
Qₜₒₜₐₗ is Qₜₒₜₐₗ: q₁ + q₂ + q₃ +………+ qₙ.
Quantisation of Charge
All free charges are integral multiples of a basic unit of charge ‘e’. The charge q of a body is given by: q = ne where n is an integer and e = 1.6 × 10⁻¹⁹ C.
Conservation of Charge
The total charge of an isolated system always remains constant.
It is impossible to create or destroy net charge in any isolated system.
Invariance of Electric Charge
Electric charge is independent of the frame of reference, meaning the charge on a body does not change regardless of its speed or the speed of the observer. Thus, Charge at rest = Charge in motion
i.e. 𝑞ᵣₑₛₜ = 𝑞ₘₒₜᵢₒₙ
Coulomb’s Law
Chapter 1 of class 12 Physics- Electric Charges and Fields” gives an in-depth understanding of the coulomb’s law. This covers-
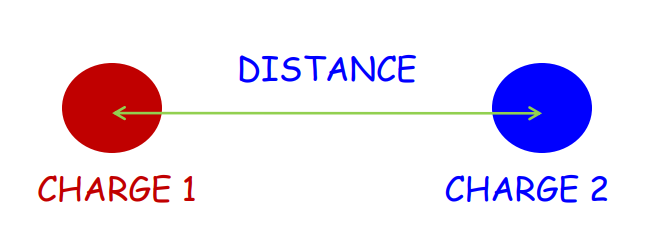
Coulomb’s Law describes the electrostatic force between two charged particles.
The Force F is:
- Directly proportional to the product of the magnitudes of the charges.
- Inversely proportional to the square of the distance between them.
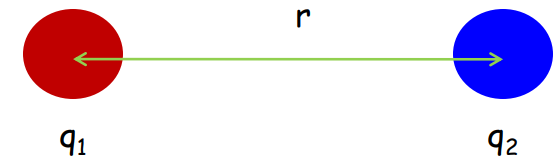
Mathematical Formulation
For charges q₁ and q₂ separated by distance r: F ∝ q₁q₂ / r².
Introducing the proportionality constant k: F = k q₁q₂ / r², where k = 4πϵ₀ and
𝜖₀ = 8.854 x 10⁻¹² C² N⁻¹ m⁻²
Vector Form
F = k q₁q₂ r/r², where r is a unit vector directed towards q₂
Nature of Coulomb Force
The nature of the coulomb force is also thoroughly discussed in the chapter Electric Charges and Fields. It covers-
- Coulomb force is directed along the straight line joining the two charges.
- The force is attractive and taken to be negative, if the charges are of opposite signs.
- The force is repulsive and taken to be positive, if the charges are of the same signs.
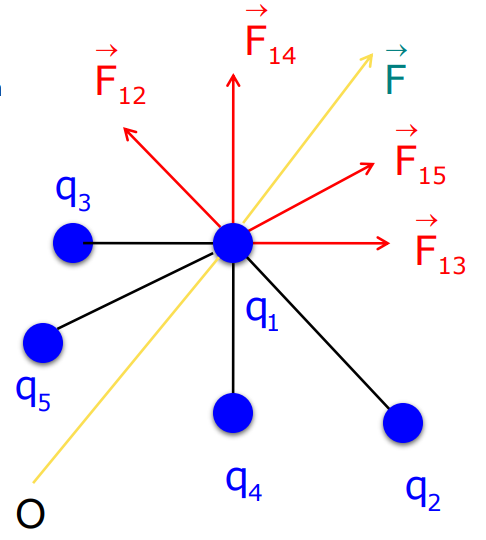
Forces Between Multiple Charges
For a system of multiple charges, as stated in the chapter Electric Charges and Fields, the total force on any charge is the vector sum of forces due to all other charges. Using the principle of superposition:
- Force on charge q₁ due to charge q₂
F₁₂= k q₁q₂ r₁₂/ r²₁₂
- Force on charge q₁ due to charge q₃
F₁₃ = k q₁q₂ r₁₃/ r²₁₃
By using the principle of superposition, the total force acting on the charge q₁ is given by:
F = F₁₂ + F₁₃
or F = k q₁q₂ r₁₂ / r²₁₂ + k q₁q₂ r₁₃ / r²₁₃
or F = k q₁q₂ / r²₁₂ r²₁₃ (r₁₂ + r₁₃)
or F = kq₁ i = 23qᵢ / r²₁ᵢ r₁ᵢ
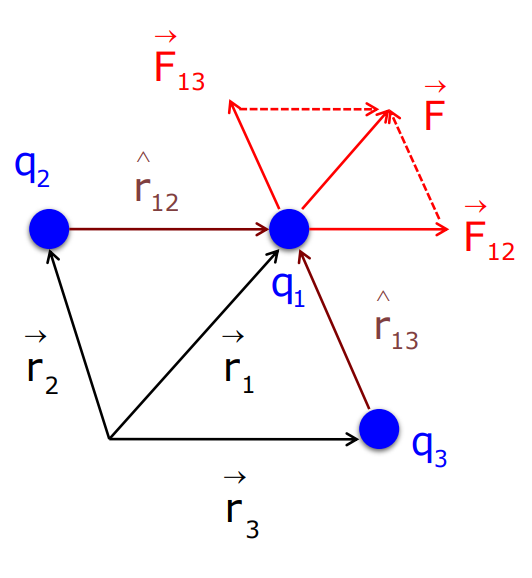
Similarly, for a system of ‘n’ charges, the total force on the charge q₁ due to various neighboring charges is
F = F₁₂ + F₁₃ + F₁₄ +……. + F₁ₙ
or F = q₁/4πϵ₀ i = 2nqᵢ / r²₁ᵢ r₁ᵢ, n = 2,3,4,……..
Electric Field
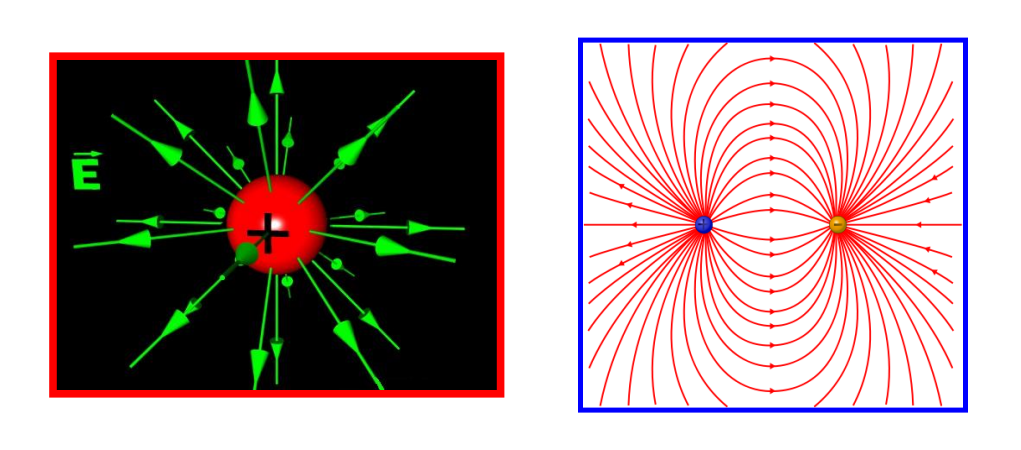
As mentioned in Physics Class 12 Chapter 1 Electric Charges and Fields, an electric field exists around a charge or system of charges, exerting electrostatic forces on other charges within that region.
Electric Field Intensity
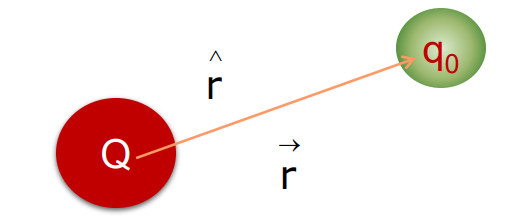
Electric field due to a charge Q at any point in space is defined as the force acting by a test charge q₀ when placed at that point, i.e.,
E= F/q₀
Coulomb’s force between the charges Q and q₀ is
F = 1/4πϵ₀ x Q q₀ r/r²
The electric field produced by the charge Q is
E = F/q₀ = Q q₀ r/4πϵ₀r² x 1/q₀ = Q r/4πϵ₀r²
E = Q r/4πϵ₀r²
It is also known as electric field strength or electric field intensity. SI unit of electric field is newton per coulomb, i.e., NC⁻¹
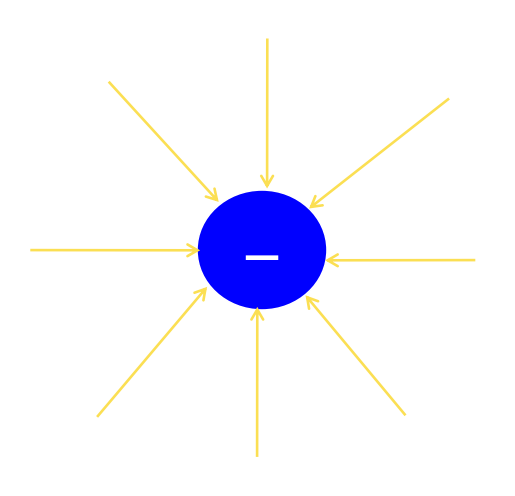
Direction and Magnitude
- The electric field will be directed radially outwards from a positive charge.
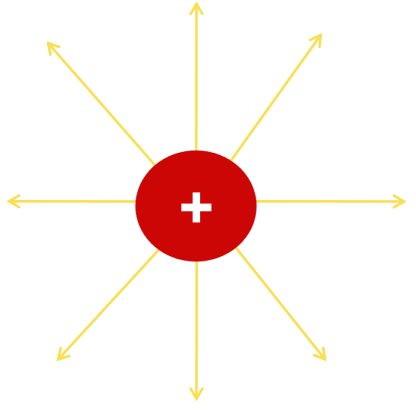
- The electric field is directed radially inwards from a negative charge.
Electric Field due to System of Charges
According to the chapter Electric Charges and Fields, In a system of four charges:
- The electric field produced by the charge q₁ at the distance r₁Q is
E₁ = Q r₁Q /4πϵ₀r²₁Q
- Similarly, the electric fields produced by the charges q₂Q, q₃Q, q₄Q are
E₂ = Q r₂Q /4πϵ₀r²₂Q
E₃ = Q r₃Q /4πϵ₀r²₃Q
E₄ = Q r₄Q /4πϵ₀r²₄Q
- The total electric field produced by the charges q₂Q, q₃Q, q₄Q
E = E₁ + E₂ + E₃ + E₄
= Q /4πϵ₀ (r₁Q / r²₁Q + r₂Q / r²₂Q + r₃Q / r²₃Q + r₄Q / r²₄Q is
E = Q /4πϵ₀ i = 14rᵢQ / r²ᵢQ
- The total electric field due to a system of n number of charges is
E = E₁ + E₂ + E₃ + E₄ + …………..+ Eₙ
E = Q /4πϵ₀ i = 1nrᵢQ / r²ᵢQ
Continuous Charge Distribution
A system of closely spaced electric charges forms a continuous charge distribution. The charge distribution is continuous in the sense that the system of closely spaced charges is equivalent to a charge, which is continuously distributed along a line on a surface or throughout a volume.
Linear Charge Density
According to class 12 physics chapter 1 – Electric Charges and Fields, If a charge ‘q’ is uniformly distributed along a line of length l, then the linear charge density is defined by:
= q/l
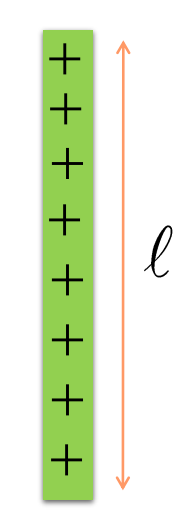
In the SI unit, it is measured in coulomb per meter (C/m).
Surface Charge Density
If a charge ‘q’ is uniformly distributed on a surface area A, then the surface charge density is defined by:
= q/A
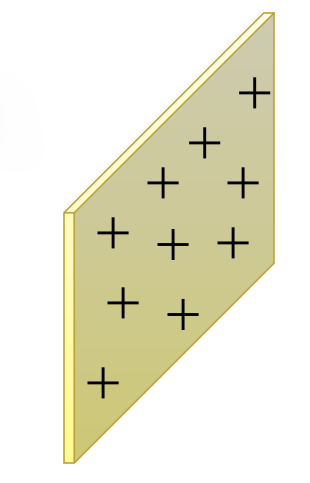
In the SI unit, it is measured in coulomb per meter (C/m²).
Volume Charge Density
If a charge ‘q’ is uniformly distributed throughout a volume V, then the volume charge density is defined by:
= q/V
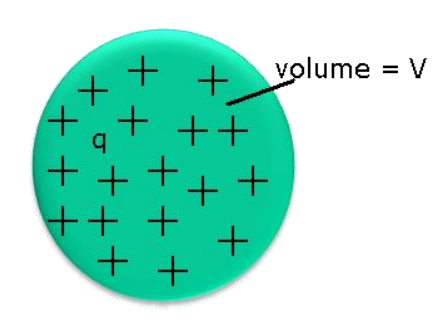
In the SI unit, it is measured in coulomb per meter (C/m³).
Electric Field Lines
The chapter Electric Charges and Fields clearly define the electric field lines. These involve
- These lines are the pictorial visualization of the electric field.
- These imaginary lines or curves are smooth and straight and are drawn in an electric field, along which, an isolated free unit positive charge moves. They describe the electrical behavior of a system of charges.
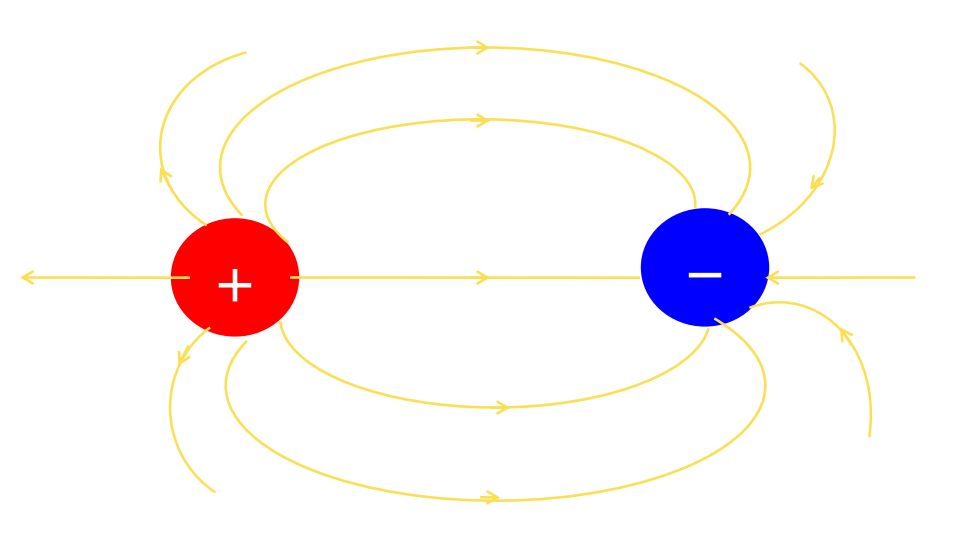
- They start with positive charges and end with negative charges. They never pass through the conductor.

- An electric field line is a curve drawn, in such a way, that the tangent to it at each point is in the direction of the net field at that point.
- The electric field lines are closer (crowded) in the region of a stronger electric field and wider apart, in the case of a weaker electric field.
- Two field lines never cross each other.
- They are continuous curves without any breaks.
- They do not form any closed loop due to the conservative nature of the electric field.
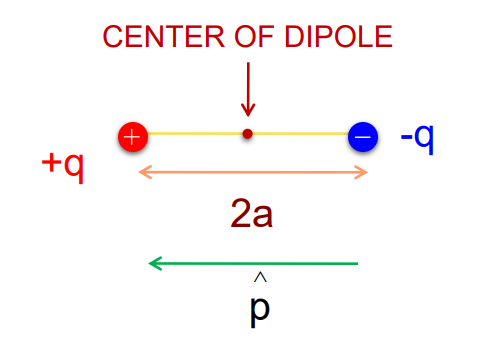
Electric Dipole
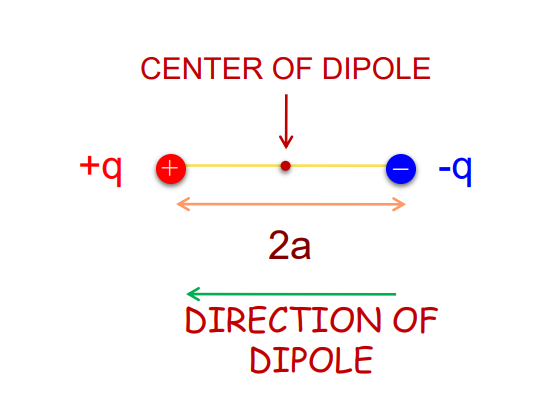
Key Points:
- It is a pair of equal and opposite point charges separated by a small distance.
- By convention, the direction of the electric dipole is from negative charges to positive charges.
- Dipole moment is defined as the product of the magnitude of one of the charges and the distance between them, i.e.
p = 2a qp
- It is a vector quantity.
- Its SI unit is cm.

Electric Field on Axial Line of a Dipole (End-on position)
- The electric field due to the negative charge of the dipole at the point P is given by:
E₋q = – q p /4πϵ₀(r + a)²
- The electric field due to the positive charge of the dipole at the point P is given by:
E₊q = – q p /4πϵ₀(r – a)²
- The total electric field at the point P is given by:
E = E₊q + E₋q
= q p /4πϵ₀ (1/ (r – a)² – 1 /(r + a)²)
Therefore, E = q p /4πϵ₀ x 4ar / (r² – a²)²

E = q p /4πϵ₀ x 4ar / (r² – a²)², ‘a’ can be change.
= 4qa p/4πϵ₀ x r/ r⁴ = 4qa p/4πϵ₀ r³
Therefore, E = 2 p /4πϵ₀r³
Since p = 2aq p
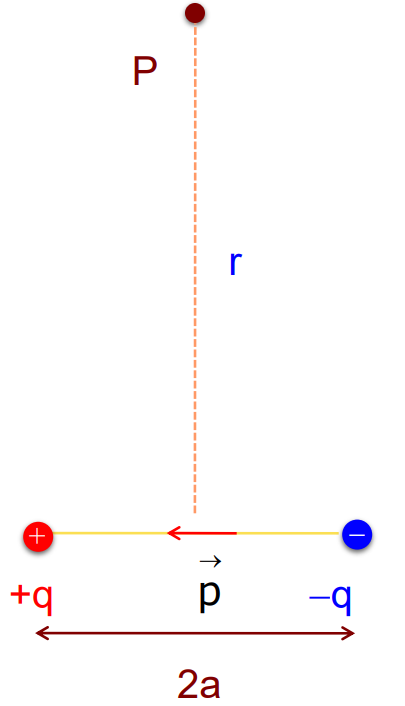
Electric Field on the Equatorial Line of a Dipole (Broad-on position)
- The magnitude of the electric field at the point P due to the positive charge is given by:
E₊q = q /4πϵ₀ (r²+ a²)
- The magnitude of the electric field along the dipole axis due to negative charges is
E₋q = q /4πϵ₀ (r²+ a²)
- The resultant electric field is opposite to the direction of the dipole.
- The component of the resultant field along the normal cancels away.
- The resultant electric field component along the dipole axis contributes to the total electric field.
E = – ( E₊q + E₋q ) cos p
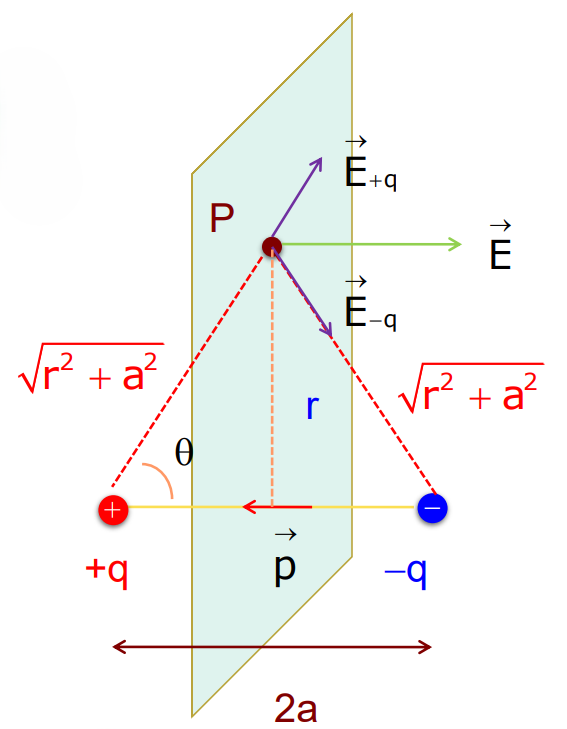
E = – (2q/4πϵ₀(a²+ r²)) cos p , where cos = a / (a²+ r²)1/2
E = – (2q/4πϵ₀(a²+ r²)) x a p / (a²+ r²)1/2
E = – 2qa p /4πϵ₀ (a²+ r²)3/2
If r >> a, E = – 2qa p /4πϵ₀ r3
Since p = 2aq p, E = – p /4πϵ₀ r3
Dipole in a Uniform External Electric Field
- Consider a dipole inclined at an angle concerning a uniform electric field.
- There are equal and opposite forces acting on the two charges of the dipole due to the uniform electric field.
- The dipole will experience a torque,
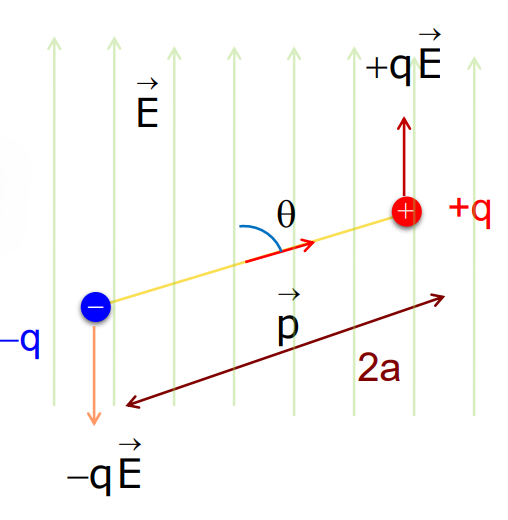
= qE 2a sin
Therefore, = p x E
Electric Flux
- In a uniform electric field, The electric flux through the area element subtending an angle q with the normal is defined as:
= E.n S = E S cos
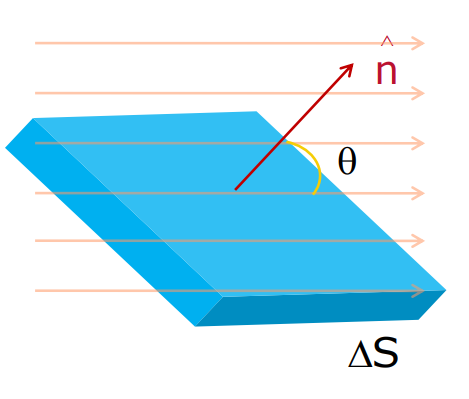
- Electric flux is the total number of electric lines of force over any closed surface.
- The total flux through the surface element is given by:
= E.n S
- The SI unit of electric flux is N C⁻¹ m².
- If the electric field is parallel to the surface, no field lines pass through the surface and the flux will be zero. The maximum flux occurs when the field is perpendicular to the surface.
Gauss’s Law
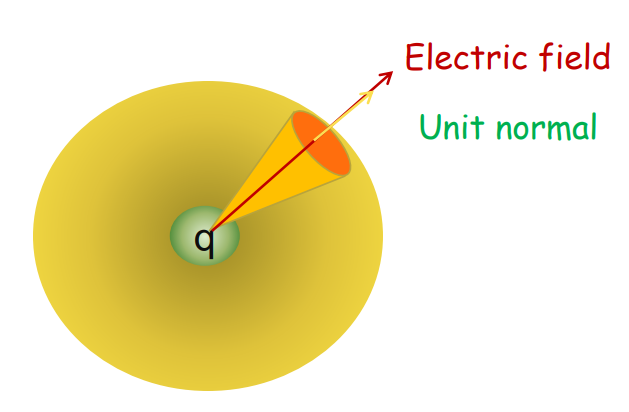
The law states that the total electric flux through a closed surface is equal to (1/∈₀) times the total charge enclosed by the surface area.
Mathematical Representation
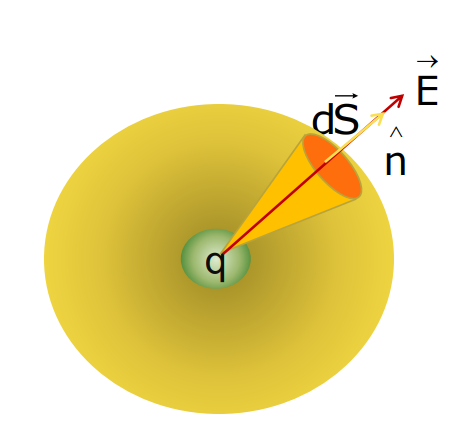
The total electric flux through the closed surface is
Therefore, =s E.DS = q /∈₀
Field due to an infinitely long straight uniformly charged wire
- Consider an infinitely long straight uniformly charged wire having charged current density l.
= q/l
- Imagine a cylindrical Gaussian surface having a radius r enclosing the charged wire.
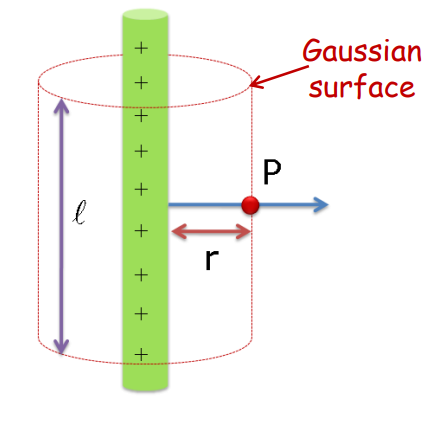
- The electric field is radially outwards.
- The electric flux from the bottom and the top of the cylinder will be zero, as the field is normal to the line of charge.
- Flux through the curved cylinder at the point P is
= E.DS = E x 2πrl
Using Gauss’s law, = q/∈₀
or, E x 2πrl = l/∈₀
E = /2πr∈₀
Field Due to a Uniformly Charged Infinite Plane Sheet
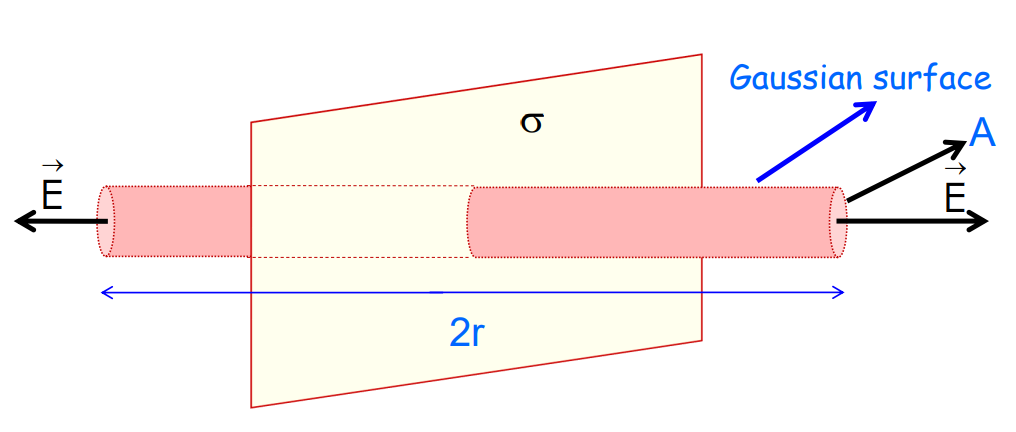
- Consider an infinite plane sheet of charge with surface charge density.
- A cylinder of length whose ends have an area A and whose walls are perpendicular to the sheet of charge is considered a Gaussian surface.
- No lines of force cross the sides of the cylinder, therefore, the component of normal to the all is zero.
- At the ends of the cylinder, the normal component E is equal to E.
- Thus, total flux through the closed surface is given by:
= E.dS = EA + EA + 0 = 2EA
- Charge enclosed by the Gaussian surface, q = A.
- According to Gauss’ law:
2EA = q/∈₀ = A/∈₀
or E = /2∈₀
Field Due to a Uniformly Charged Thin Spherical Shell
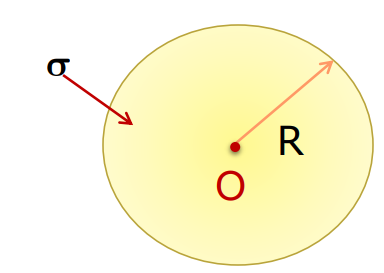
- Consider a thin charged spherical shell of radius R. Let its surface charge density be.
- The field outside, inside, and at the surface of the shell will depend on the radial distance from the center to the point of consideration.
Outside the shell
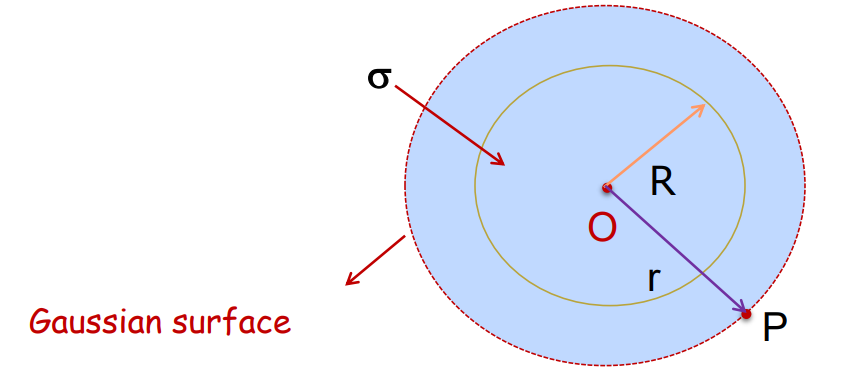
- Consider a spherical Gaussian surface having radius r passing through the point P.
- The total electric flux through the Gaussian surface is
= E x 4πr²
- The charge enclosed is given by:
q = x 4πr²
By Gauss’s law, = q/∈₀
or E x 4πr² = 4πR²/∈₀
E = q/4π∈₀ r² (Therefore, = q/4πR²)
On the surface of the shell
- At point ‘r’ outside the thin spherical shell, the electric field is given by:
E = q /4π∈₀ r²
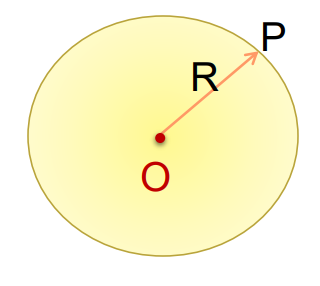
- At point P(r = R), the electric field is given by:
E = q /4π∈₀ R²
or, E = x 4πR² / 4π∈₀ R² = /∈₀ (q = x 4πR²)
Inside the shell
- Inside the spherical charged shell, the Gaussian surface lies inside the sphere with radius r
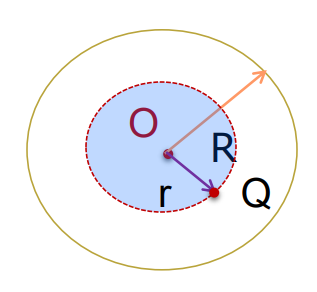
Applying Gauss’s law,
= E.dS = q / ∈₀
Inside the Gaussian surface, there is no charge, i.e.,
q = 0
E.dS = 0/∈₀ = 0
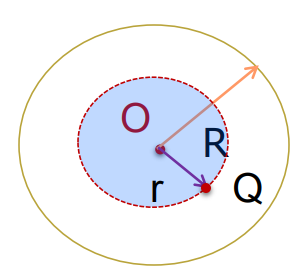
The electric field due to a uniformly charged thin shell is zero at all points inside the shell.
Conclusion
In conclusion, Chapter 1 of CBSE Class 12th Physics, Electric Charges and Fields, lays the foundation for understanding the intricate behavior of electric charges and the forces they exert in nature. By exploring the fundamental concepts of electrostatics, this chapter highlights key principles like Coulomb’s Law, the concept of electric fields, and the methods of charging. From understanding electric charge interactions to calculating the forces between multiple charges, this chapter provides a detailed framework for students preparing for their board exams.
At iPrep, we have enriched your learning experience with engaging videos, comprehensive notes, and practical questions to help you master the chapter Electric Charges and Fields for Class 12th Physics. Our learning resources are tailored to ensure that you grasp complex concepts with ease, ensuring a thorough preparation for all your Physics needs. Remember, with iPrep’s integrated learning, studying Electric Charges and Fields in CBSE Class 12th Physics becomes both efficient and enjoyable, setting a strong foundation for your future academic success.
Practice questions on Chapter 1 - Electric Charges and Fields
Get your free Chapter 1 - Electric Charges and Fields practice quiz of 20+ questions & detailed solutions
Practice Now








