Electrostatic Potential and Capacitance – Complete Guide For Class 12 Physics Chapter 2

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Electrostatic Potential and Capacitance in Physics for Class 12th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples. 

The chapter Electrostatic Potential and Capacitance explores the fundamental concepts of electrostatics, focusing on the potential created by static charges and the capacity of materials to store electric charge. The chapter covers the definition and calculation of electrostatic potential, the potential due to point charges and electric dipoles, and the concept of equipotential surfaces. It also delves into the potential energy of systems of charges and the behavior of dielectrics in electric fields. Furthermore, it explains the principles and calculations related to capacitors, including their configurations in series and parallel, and the energy stored in capacitors. The chapter concludes with an understanding of the Van de Graaff generator, which demonstrates the practical application of electrostatic principles to generate high voltages.

Electrostatic Potential and Capacitance

In this chapter, we delve into the principles of electrostatics, focusing on the potential created by static charges and the capacity of different materials to store electric charge.

Introduction

• The electrostatic potential of a body determines the degree of electrification of the body.  
• The charge flows from a body at a higher potential to another body at a lower potential. 
• The capacitance of a capacitor is the amount of charge required to raise its potential by unity.  
• A capacitor is a device that stores energy as potential energy in an electric field.

Electrostatic Potential

Let’s uncover the definition of the Electrostatic Potential from the chapter Electrostatic Potential and Capacitance.

Definition: The electrostatic potential of a body determines the degree of electrification. The charge flows from a body at a higher potential to another body at a lower potential.

Electrostatic Potential at a Point: It is the minimum work done in carrying a unit positive charge (without acceleration) from infinity to that point.

Capacitance

Let’s us now over the definition of Capacitance from Class 12 Physics Chapter 2- Electrostatic Potential and Capacitance.

Definition: Capacitance of a capacitor is the amount of charge required to raise its potential by unity. It is a device that stores energy as potential energy in an electric field.

Key Concepts

Electric Potential Due to a Point Charge

The electric potential V at a point with position vector r due to a point charge q placed at the origin is given by: 

V_(r) = 1/ 4πϵ₀ x q /r

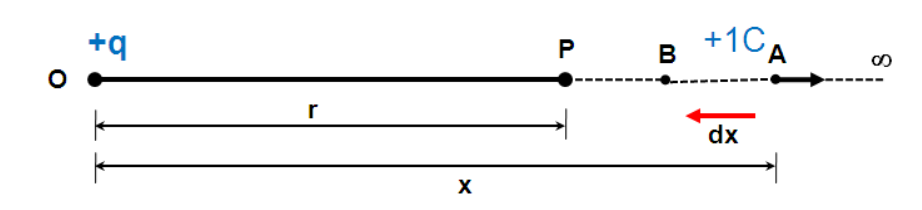
Potential Due to an Electric Dipole

For an electric dipole with charges −q and +q separated by a distance 2a, the potential V at a point P with position vector r is: 

V_(r) = 1/ 4πϵ₀ x p. r/r³ for r>>a

where p = q × 2a is the dipole moment.

The dipole moment |p| = q x 2a

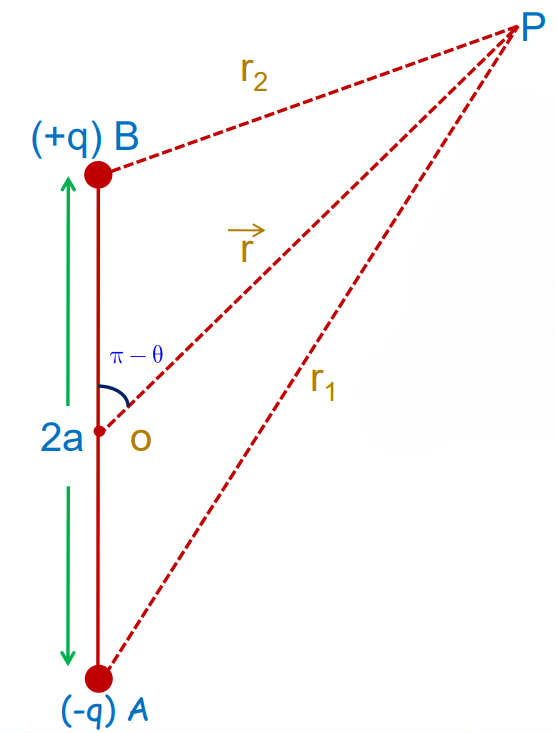
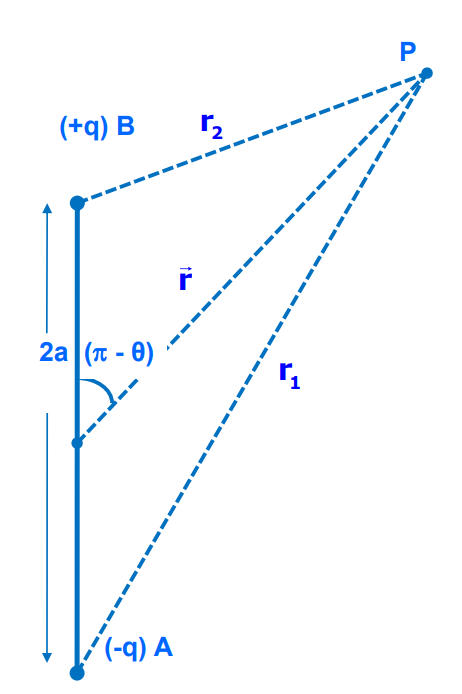
Potential at P due to -q,   V₁ = -q/4πϵ₀ r₁

Potential at P due to +q,  V₂ = q/4πϵ₀ r₂

Potential at P due to dipole is, V = V₁ + V₂ 

                                             V = p cos θ /4πϵ₀ r²

Potential Due to a System of Charges

For multiple charges 𝑞₁, q₂,……..qₙ at distances r₁, r₂,……..rₙ respectively from the point P, the potential is: V = 1/ 4𝜋𝜖₀ i = 1n qᵢ/rᵢ

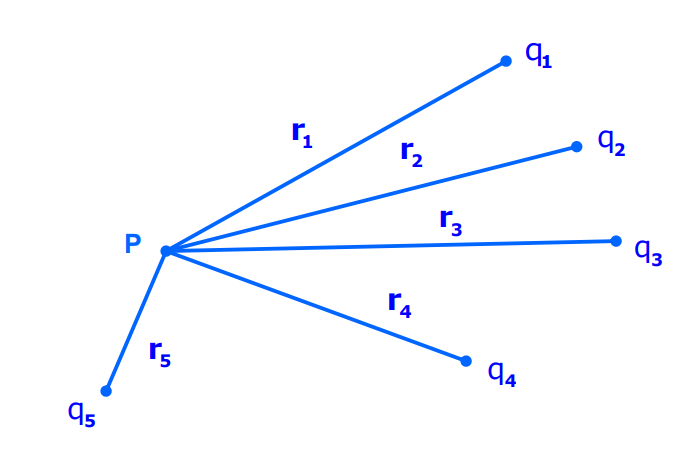
Keypoints for Point Charges

• The sum is an algebraic sum, not a vector sum.
• E may be zero, where V is not equal to zero.
• V may be zero, Where E is not equal to zero.

Equipotential Surfaces

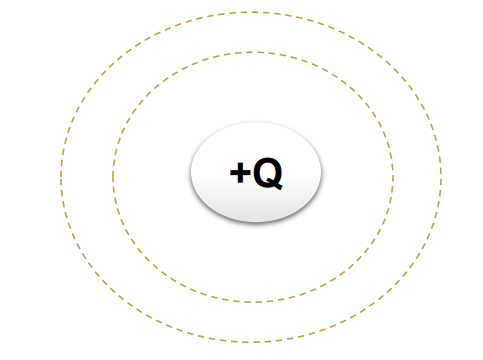
Definition: Equipotential surfaces have the same potential at all points on the surface.

Example: (a) Equipotential surfaces of a single-point charge are spherical surfaces centered at the charge. 

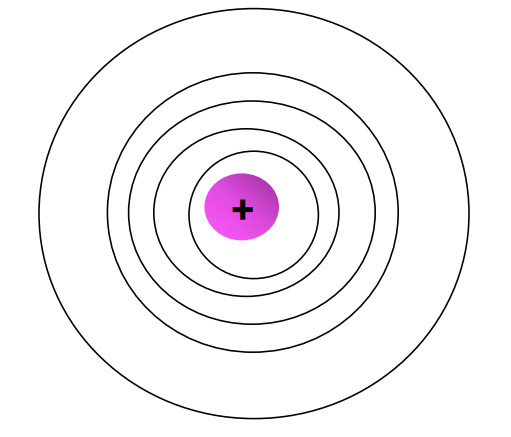
(b) Electric field lines are radial, starting from the charge if q > 0.

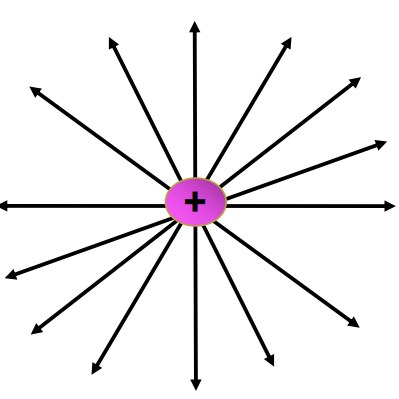
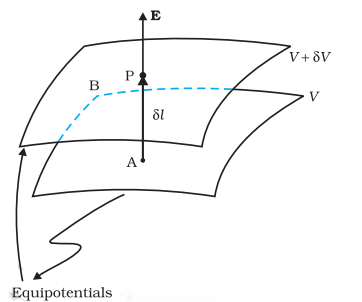
Relation between Field and Potential

|E| = – V/l = + |V|/l

Potential Energy of a System of Charges

The potential energy U of a system of two charges q₁ and q₂ separated by a distance r₁₂ is: 

U = 1x q₁.q₂/4πϵ₀ x r₁₂

​

The potential energy (U) of a system of charges q₁ and q₂ is directly proportional to the product of charges and inversely to the distance between them.

Potential Energy of a Single Charge in an External Field

If V_(r) is external potential at any point P of the position vector then by definition, work done in bringing a unit positive charge from infinity to the point P in the external field is q.V_(r).

Potential Energy of Two Charges in an External Field

If q₁, q₂ are two point charges at position vectors r₁ and r₂ in a uniform external field of intensity E, then : 

                 U = q₁.V_(r₁₎ + q₂.V_(r₂₎ + 1/ 4𝜋𝜖₀ x q₁, q₂/r₁₂

Potential Energy of Dipole in an External Field

The potential energy of dipole moment p in a uniform electric field E is given by

U = –  p.E

The potential energy of an electric dipole in an electrostatic field is defined as the work done in rotating the dipole from the zero energy position to the desired position in the field.  

The zero energy position is when the dipole is at right angles to the lines of force of the electric field.

Electrostatics of Conductors 

Let’s go deeper into the chapter Electrostatic Potential and Capacitance, and understand the concepts of Electrostatics Of Conductors. These involve-

• Inside a conductor, the electric field is zero.  
• At the surface of a charged conductor, the electrostatic field must be normal to the surface at every point.

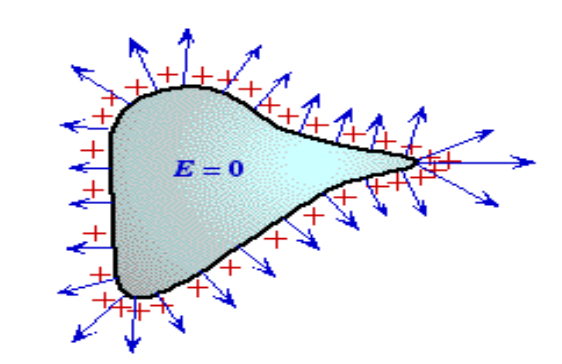
• The interior of a conductor can have no excess charge in the static situation.  
• The electrostatic potential is constant throughout the volume of the conductor and has the same value as on its surface.
• The electric field at the surface of a charged conductor is

                         E = /ϵ₀ . n

• Where, is the surface charge density and n is a unit vector normal to the surface in the outward direction

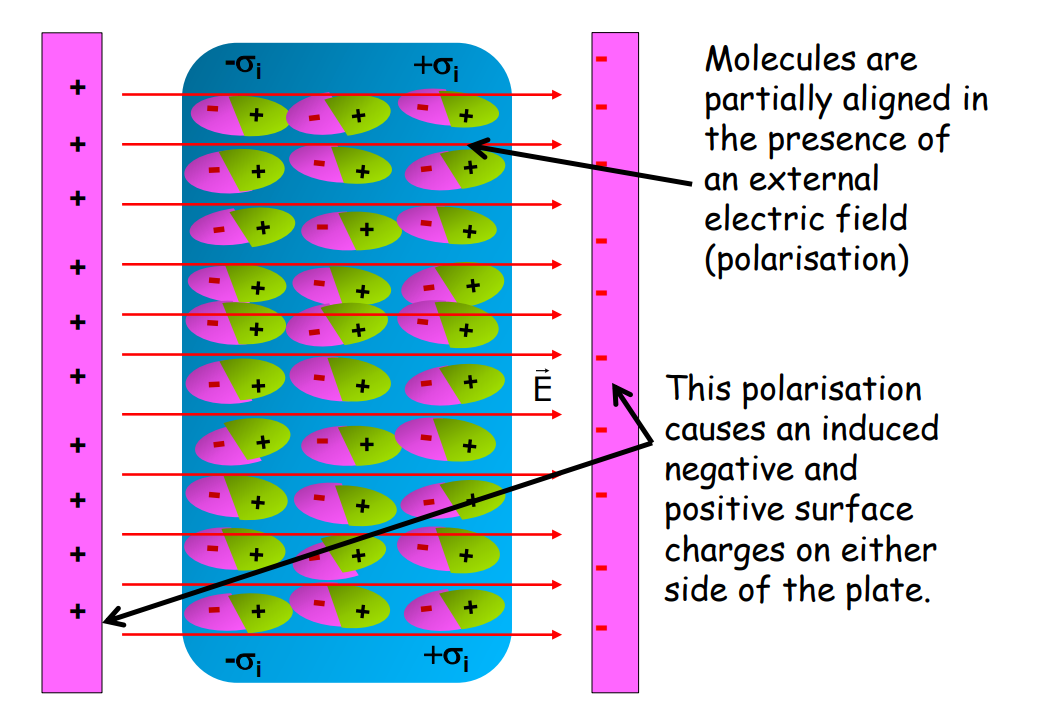
Dielectrics and Polarization

In this part of the chapter Electrostatic Potential and Capacitance, we’ll cover Dielectrics and Polarization.

Dielectrics

Materials that do not allow current to flow through them are called Dielectrics.

• The electrons in such materials remain bound within their molecules, thus preserving the overall neutrality of each molecule.  
• They are affected by external electric fields because the positive and negative charges tend to shift in opposite directions & thus transmit electrical effects.

Polar and Non-polar Molecules  

The molecules of a substance may be: Polar or Non-polar

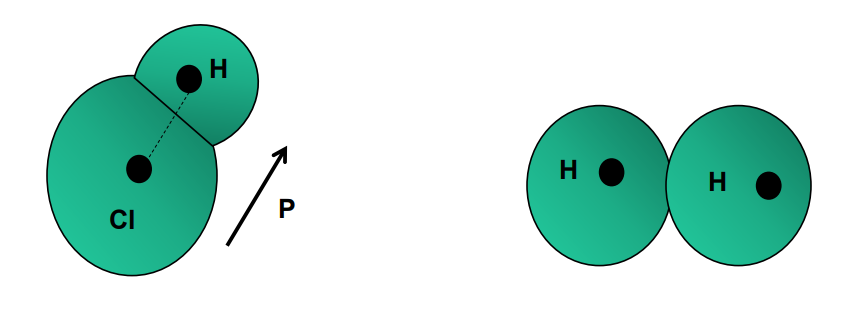
Non-Polar Molecules 

In molecules such as hydrogen, and oxygen, the center of positive charge coincides with the centre of negative charge in the molecule. Each molecule has zero dipole moment and is symmetric in shape.

Polar Molecules

In molecules of water and alcohol, the centers of the positive and negative charges do not coincide as the shape of the molecules is asymmetric.

Polarization

The chapter Electrostatic Potential and Capacitance also thoroughly covers the concept of polarization. This covers-

• In an external electric field, the positive and negative charges in a dielectric material shift in opposite directions, creating an induced dipole moment.
• The dielectric material is said to be polarised.

• For a dielectric with a polar molecule, in the absence of an electric field, the dipoles are oriented randomly because of thermal agitation.  
• So, the total dipole moment is zero.

• When an external field is applied, the individual dipole moments tend to align with the field. Hence, there is a dipole moment in the direction of the field.  
• Dielectric is said to be polarised.

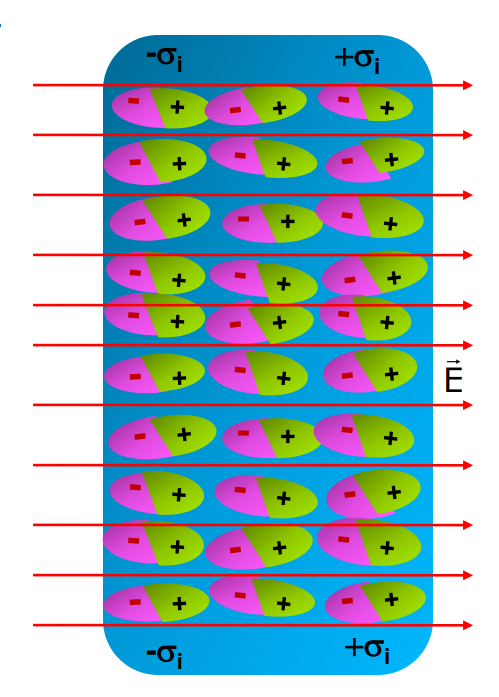
Molecular Model of the Induced Charge 

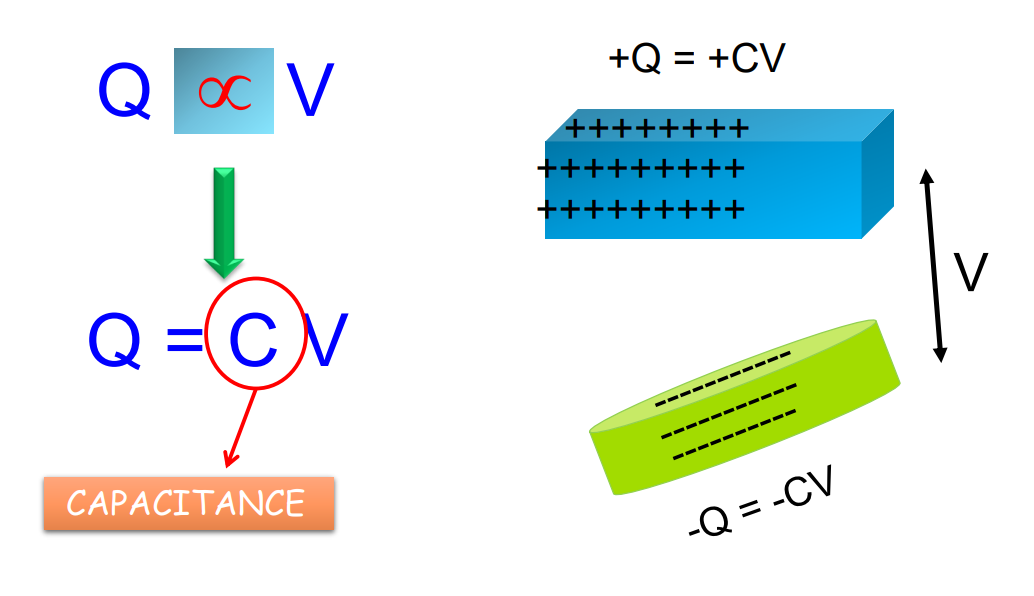
Capacitor

Any two conductors form a capacitor when carrying opposite charges of equal magnitude and separated by a dielectric.

Capacitance: The ratio of the magnitude of charge on one conductor to the potential difference between conductors. 

                                    C = V/Q

​

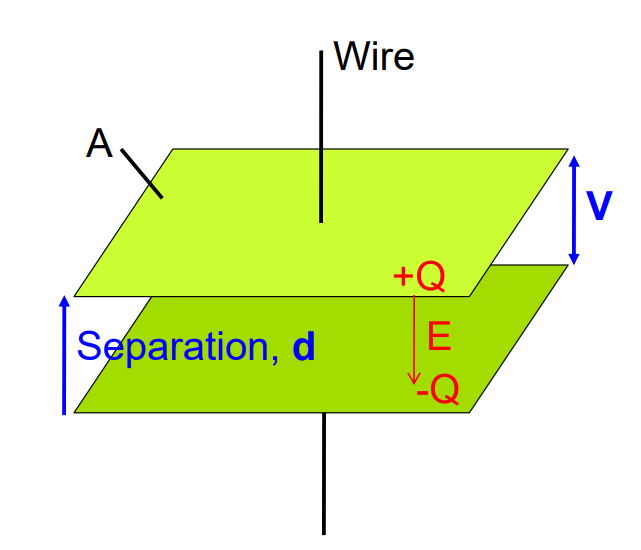
Parallel Plate Capacitor: Consists of two large plane conducting plates separated by a small distance. 

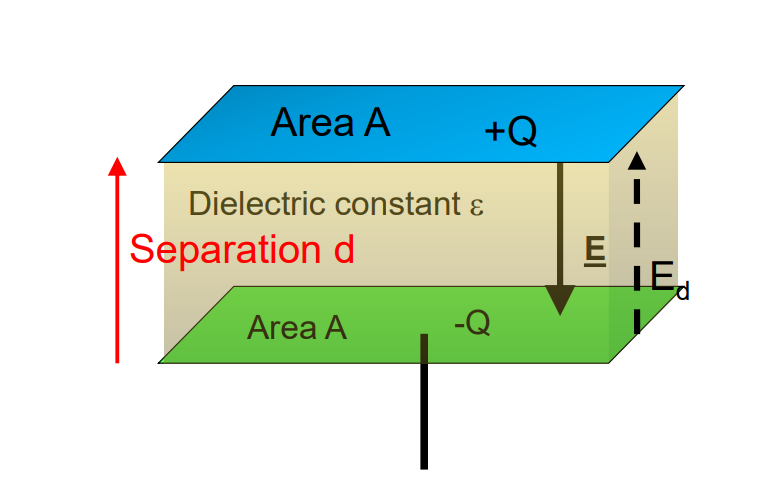
When a dielectric medium is introduced, its capacitance increases by a factor of the dielectric constant K.

Effect of Di-electric on Parallel Plate Capacitor

When plates of a capacitor are separated by a dielectric medium of relative permittivity eᵣ = K, its capacitance Cₘ increases from its value C₀ (when there is no medium) by the relation: 

                            Cₘ = KC₀

Parallel Plate Capacitor with Dielectric

When Capacitors are connected in Series

The reciprocal of the equivalent capacitance is the sum of the reciprocals of individual capacitances.

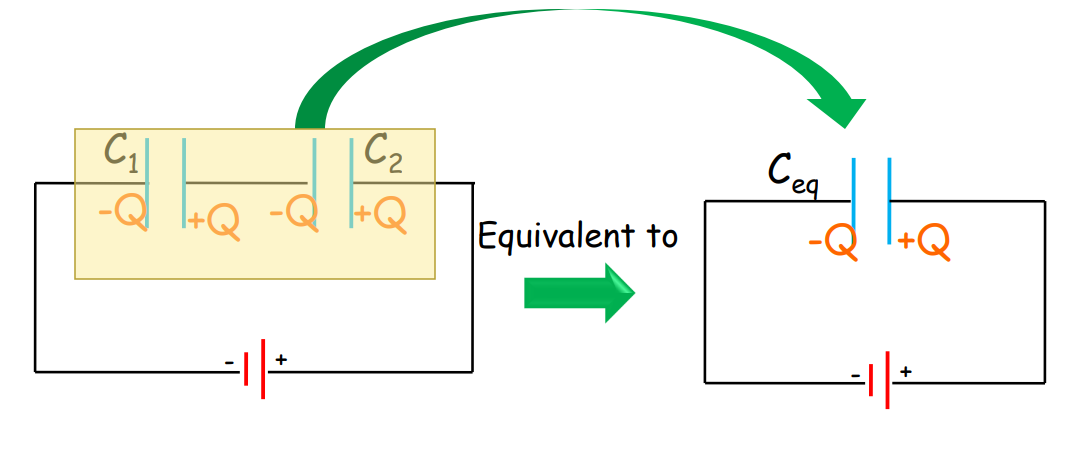
The equivalent capacitance: 1/C_eq = 1/C₁ + 1/C₂

n Number of Capacitors connected in Series

The equivalent capacitance of the n number of capacitors connected in series is 

                      1/C_eq = i = 1n1/Cᵢ

When Capacitors are connected in Parallel

 The equivalent capacitance is the sum of individual capacitances.

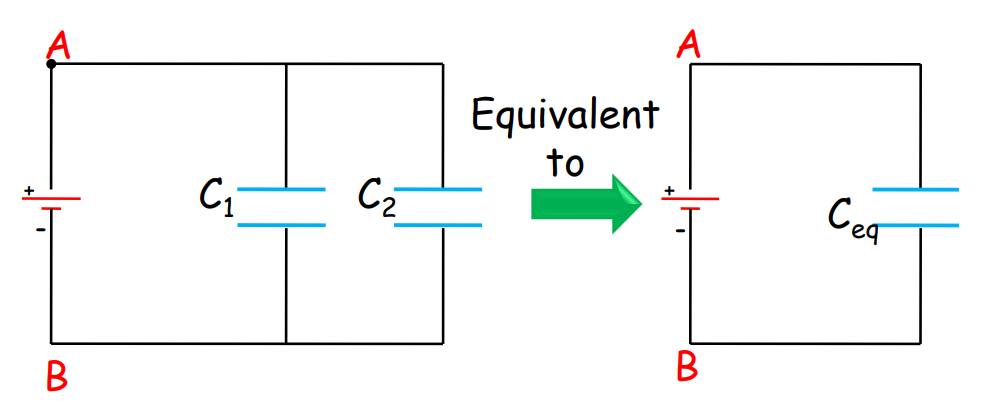
The equivalent capacitance: C_eq = C₁ + C₂

n Number of Capacitors connected in Parallel

The equivalent capacitance of the n number of capacitors connected in parallel is 

                      C_eq = i = 1nCᵢ

Energy Stored in a Capacitor

The total work done to charge the conductor to Q is,

                     W = Q²/2C

The energy U stored in a capacitor with capacitance C and voltage V is: 

                       U = 1/2 x CV² = Q²/2C = 1/2 QV

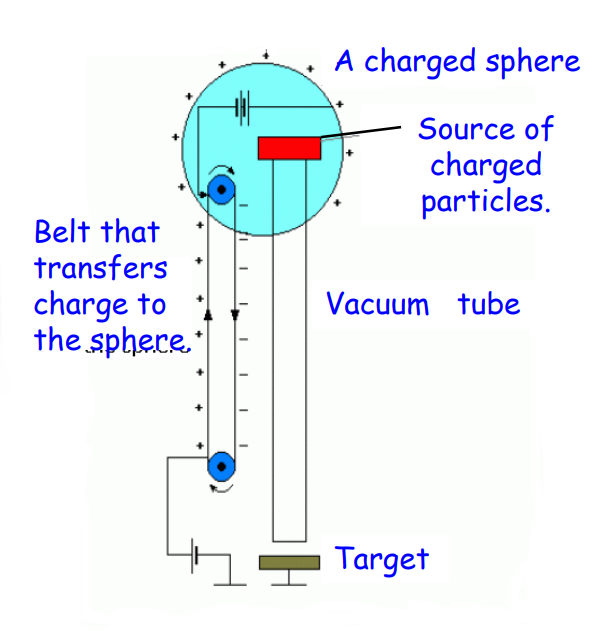
Van de Graaff Generator

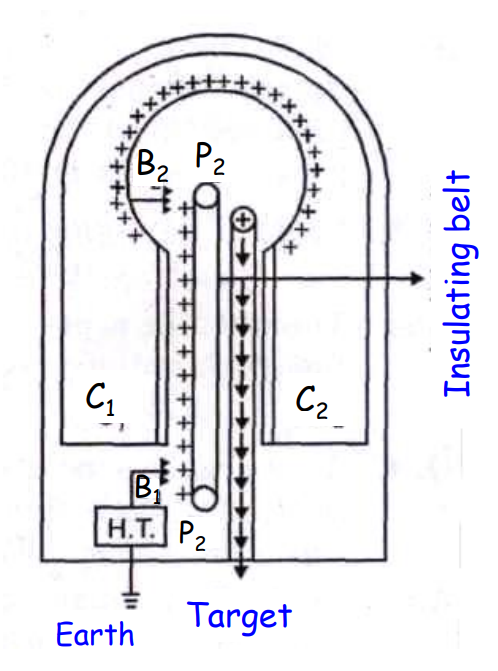
Principle of Van De Graaff Generator

It is based on  

• The phenomenon of Corona discharge.  
• The property that charge given to a hollow spherical conductor is transferred to the outer surface and is distributed uniformly over it.

Working Principle of  Van de Graaff Generator

Mechanism:

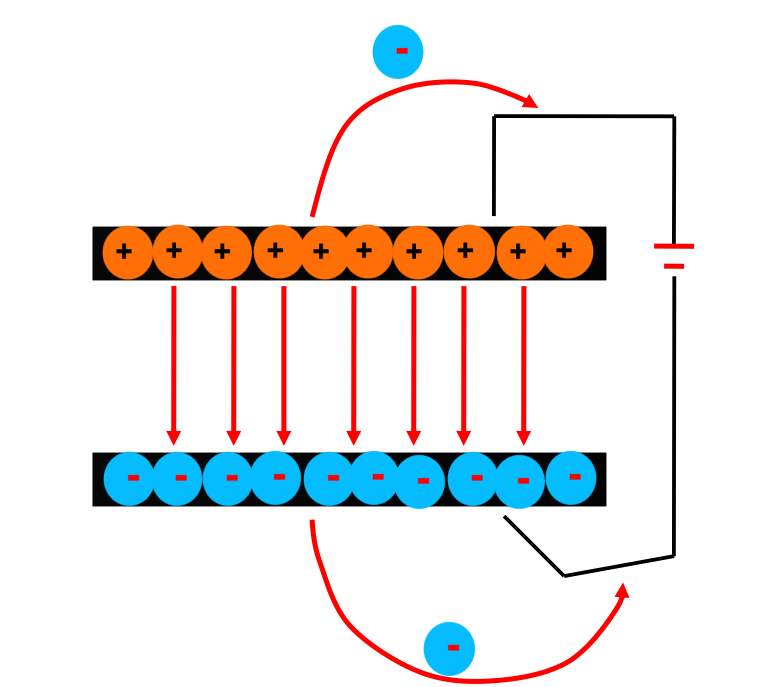
• As the belt moves and reaches the sphere, a negative charge is induced on the sharp ends of the second comb, as a result of which an equal positive charge is induced on the farther end of the second comb.  
• The positive charge shifts immediately to the outer surface of a sphere. 
• The comb is given a positive potential of nearly 104 volts.  
• Due to the discharging action of the sharp points, a positive charge gets sprayed on the belt.
• Due to the discharging action of the second comb, a negatively charged wind is set up which neutralizes the positive charge on the belt. 
•  The uncharged belt returns down and collects the positive charge from the first comb.

The process repeats. Thus, the positive charge goes on accumulating.  

The capacitance of the spherical shell is given by:  C = 4₀R and the potential developed is given by: V = Q/4₀R.

Conclusion

In CBSE Class 12th Physics, Chapter 2 – Electrostatic Potential and Capacitance, we have explored the essential concepts that define how electric charges interact and how energy is stored within electric fields. This chapter provides a comprehensive understanding of electrostatic potential, emphasizing the importance of charge distribution and the behavior of materials in electric fields.

By mastering the principles discussed in this chapter, including the relationship between potential and capacitance, students will be better equipped to tackle more complex topics in electromagnetism. Additionally, the applications of electrostatics, such as in capacitors and the Van de Graaff generator, showcase the practical relevance of these concepts in modern technology.

In summary, Electrostatic Potential and Capacitance is not just a chapter in your physics syllabus; it is a foundational element that connects various fields of study and paves the way for future explorations in physics and engineering. We encourage you to continue your journey in CBSE Class 12th Physics by diving deeper into these concepts and their real-world applications. Remember, the more you engage with these ideas, the clearer your understanding will become. Keep experimenting and learning!