Cubes and Cube Roots – Complete Guide Of Class 8 Math Chapter 7

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Cubes and Cube Roots in Mathematics Class 8th Chapter 7 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

Chapter 7, “Cubes and Cube Roots,” explores the concept of perfect cubes, properties of cube numbers, and methods to find cube roots. It includes both manual calculations and practical applications, enhancing students’ understanding of three-dimensional mathematics and preparing them for advanced topics in algebra and geometry.

Understanding cubes and cube roots is fundamental in mathematics. This chapter explores the concept of cube numbers, where a number is multiplied by itself three times. Here’s a quick glance:

• 1 x 1 x 1 = 1³
• 2 x 2 x 2 = 2³
• 5 x 5 x 5 = 5³
• 10 x 10 x 10 = 10³
• 12 x 12 x 12 = 12³

These are known as cube numbers.

Defining Cubes

In the chapter Cubes and cubes roots of class 8 we will first learn about cubes and then cube roots.

In general terms:

• For a number ‘a’, the cube is given by: a³ = a×a×a

Thus, the cube of a number is that number raised to the power of three.

Examples of Cubes

• Example 1:  2×2×2=8
• Example 2:  3×3×3=27

This means 27 objects can be arranged into a cube of 3 rows and 3 columns.

Perfect Cubes

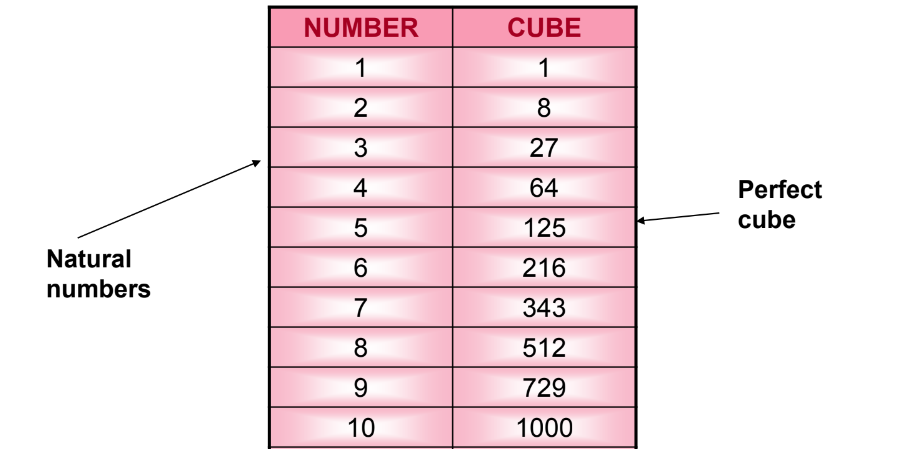
A perfect cube is a natural number that can be expressed as the cube of another natural number, n = m³.

Natural Numbers as Perfect Cubes

given here are some of the examples of the natural numbers that are also perfect cubes.

Properties of Cubes

1. Even Numbers’ Cubes are Even
   Examples:
   • 6³ = 216
   • 8³ = 512
   • 10³ = 1000
2. Odd Numbers’ Cubes are Odd
   Examples:
   • 5³ = 125
   • 7³ = 343
   • 9³ = 729
3. The sum of Cubes Formula
   The sum of the cubes of the first n natural numbers equals the square of their sum: 

1² + 2²+…+n² = (1+2+…+n)²

4. Cubes of Negative Numbers
   • (-a)³ = -a³

Examples:

• (-1)³ = -1
• (-5)³ = -125

Cubes of Rational Numbers

For a rational number m/n:

(m/n)³ = m³/n³​

Examples:

• (1/2)³ = 1/8​
• (−6/35)³ = −216/42875

Patterns in Cubes

• Adding Consecutive Odd Numbers
  Examples:
  • 1 = 1³
  • 3 + 5 = 8 = 2³
  • 7 + 9 + 11 = 27 = 3³
• Difference of Cubes
  a³ − b³ = 1+3 × a × b
  Examples:
  • 3³ − 2³ = 1+3×3×2 = 19
  • 5³ − 4³ = 1+3×5×4 = 61

Prime Factorization and Cubes

• Prime Factorization of 125
  125 = 5×5×5 = 5³ 
• Prime Factorization of 216
  216 = 2×2×2×3×3×3 = (2×3)³ = 6³

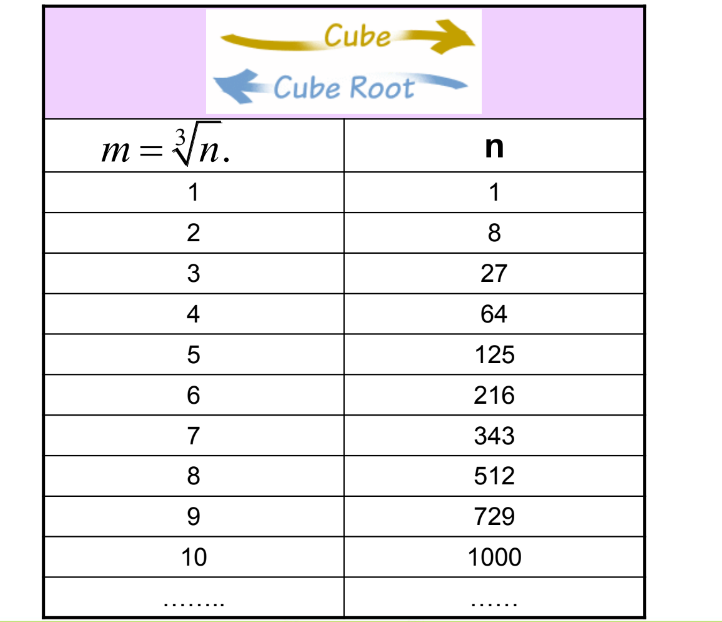
Cube Root

Now that we know very well about the cubes we will now learn to find the cube roots.

Cube root is the inverse operation of the cube:

• A number ‘a’ is the cube root of b if b=a³.

This symbol denotes CUBE ROOT: ∛​

Cube Root by Prime Factorization

To find the cube root:

1. Find the prime factorization of the number.
2. Group the factors in triples. If a prime factor is left ungrouped, the number is not a perfect cube. Otherwise, the product of one factor from each group gives the cube root.

Examples:

• 13824
  Prime factorization: 13824 = 2×2×2×2×2×2×2×2×2×3×3×3
  Cube root: ∛138243 = 24
• 55296
  Prime factorization: 55296=2×2×2×2×2×3×3×3×4×4×4
  This is not a perfect cube.

Cube Root of a Negative Perfect Cube

For a negative perfect cube:

• (−a)³ = −a³
• ∛−a³= −a 

Example:

• ∛−17283 = −12 

Cube Root of Product of Two Integers

For any two integers a and b:

∛ab = ∛a × ∛b

Example:

• ∛8×13313 = 2×11 = 22

Cube Root of a Rational Number

For any rational number a/b​:

∛a/b = ∛a/∛b​​

Example:

• ∛27/64 = 3/4​

This chapter offers a thorough exploration of cubes and cube roots, covering the basic principles, properties, and various methods for finding cube roots, including practical applications with rational numbers.