Direct And Inverse Proportions – Complete Guide For Class 8 Math Chapter 11

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Direct and Inverse Proportions in Mathematics Class 8th Chapter 11 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

Chapter 11 in class 8 covers direct and inverse proportions. In direct proportion, two quantities increase or decrease together, maintaining a constant ratio. In inverse proportion, one quantity increases while the other decreases, keeping their product constant. These concepts are crucial for understanding relationships in real-life scenarios.

Let’s start with chapter 11 of Class 8 Mathematics, where we delve into the fascinating concepts of direct and inverse proportions. Understanding these relationships is essential for grasping how quantities interact with each other in various situations.

Introduction: What Are Direct and Inverse Proportions?

Mathematics is all about understanding relationships between quantities. Two key types of relationships are direct and inverse proportions:

• Direct Proportion: When two quantities increase or decrease together, keeping a constant ratio.
  
  
• Inverse Proportion: When one quantity increases while the other decreases, such that their product remains constant.
  
  

These ideas are not just theoretical—they apply to everyday situations like calculating expenses or understanding speed and travel time.

Direct Proportion

Imagine a petrol pump scenario. As you buy more petrol, your car can travel further. This situation perfectly illustrates direct proportion: as one quantity increases, the other increases proportionally. For example, the more petrol you purchase, the further you can travel.

Understanding Direct Proportion

In direct proportion, an increase or decrease in one quantity causes a corresponding increase or decrease in another. This relationship is defined by a constant ratio. Consider the following example:

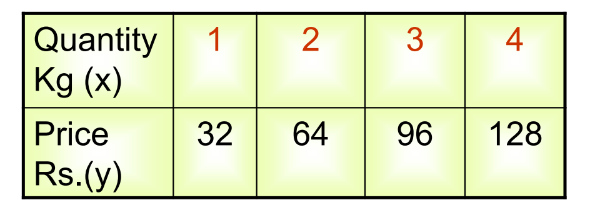
Here, as the quantity of rice increases, the price also increases, maintaining a constant ratio (1/32).

Methods to Solve Direct Proportion Problems

Unitary Method

1. Find the cost or value of one unit.
   
   
2. Multiply the one-unit value by the desired number of units.
   
   

Example:
If 5 pencils cost Rs 25, then the cost of 12 pencils is determined by:

• Cost of 1 pencil = 25 ÷ 5 = Rs 5
  
  
• Cost of 12 pencils = 5 × 12 = Rs 60
  
  

Ratio Method (Proportion Rule)

This method uses the equation:

x1/y1  =  x2/y2

Example:
If 3 kg of rice cost Rs 120, to find the cost of 8 kg, set up the ratio:

3/120   = 8/x

Solving for x gives:

x=8×120/3 = Rs320

Applications of Direct Proportions

Let’s explore some practical applications:

1. Cost Calculation: If 7 kg of sugar costs Rs 147, then the cost of 12 kg can be calculated using either the unitary or tabular method. Both methods yield Rs 252.
2. Balloon Purchase: If 50 balloons cost Rs 45, then for Rs 27, Mannat can buy 30 balloons.
3. Water for Tea: Mary needs 300 ml of water for 2 people; for 5 people, she needs 750 ml, hence an additional 250 ml.

In real life, direct proportion examples include:

• More commodities purchased, more cash required.
• More homework, more time needed.
• More visitors, more seats occupied.

Identifying Direct Proportions

To determine if quantities are in direct proportion, check if their ratios remain constant. For instance:

In the first table above, the ratio of x to y is consistent (1/3), indicating a direct proportion.
However, if the ratio varies as in the second table, the quantities are not in direct proportion.

Real-Life Direct Proportion Problems

Consider the cost of clothing:

• 7 meters cost Rs 350.
• Using this, calculate the cost for 3, 5, 8, and 12 meters.

Or, if a recipe requires certain ingredients for 5 people, calculate the amounts needed for 35 people, scaling up proportionally.

Practice Problems on Direct Proportion

1. If 10 books cost Rs 500, what is the cost for 15 books?
   
   
2. A car consumes 8 liters of fuel for 120 km. How much fuel is needed for 300 km?
   
   
3. If a train travels 240 km in 4 hours, how far will it travel in 6 hours?
   
   
   

Inverse Proportion

In inverse proportion, the increase in one quantity results in a decrease in another, maintaining a constant product. For example:

• More people can complete a task faster.
• A car traveling faster reaches the destination sooner.

Understanding Inverse Proportion

Consider an organization buying books. If the budget is fixed at Rs 50,000:

• More expensive books mean fewer books can be bought.

This relationship can be generalized: if x1 and x2 are two values of one variable and y1 and y2 are corresponding values of another, then x1y1 = x2y2 = k, where k is a constant.

Examples of Inverse Proportion

1. Speed and Time: A car at 75 km/hr takes 40 minutes to reach a destination. Reducing the speed to 50 km/hr increases the time to 60 minutes.
2. Leakages in a Tank: More leakages empty the tank faster. Repairing two out of six increases the time needed to empty the tank.
3. School Periods: If a school has 8 periods of 45 minutes each, increasing to 9 periods shortens each to 40 minutes, assuming the total school time remains constant.

Method to Solve Inverse Proportion Problems

The relationship for inverse proportions is given by:

x1 × y1=x2 × y2

Example:
If 4 men take 12 days to complete a job, then to find out how long 6 men would take:

4 × 12=6 × x

Solving for x:

x=4 × 12 / 6= 8 days

Practice Problems on Inverse Proportion

1. If 8 taps fill a tank in 3 hours, how long will 4 taps take?
   
   
2. A car takes 6 hours to travel a distance at 50 km/hr. How long will it take at 75 km/hr?
   
   
3. If 15 workers complete a task in 12 days, how many days will it take for 10 workers?

This chapter Direct And Inverse Proportions helps students understand these fundamental concepts and their applications, crucial for solving real-world problems and mathematical equations.

To read the NCERT text of the CBSE class 8 Maths chapter Direct and Inverse Proportions, click here.

To read our notes for the next chapter in class 8 Maths, Exponents and Powers, click here.