Mensuration – Complete Guide For Class 8 Math Chapter 11

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Mensuration in Mathematics Class 8th chapter 9 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

Mensuration explores the measurement of shapes. Learn to calculate areas and perimeters of 2D figures like triangles, squares, rectangles, circles, and quadrilaterals. Understand the concept of surface area and volume for 3D shapes like cubes, cuboids, and cylinders. Apply these concepts to real-world problems.

Introduction to Mensuration

In this chapter, we’ll explore the fascinating world of mensuration for class 8 in chapter 9, a branch of mathematics dealing with the measurement of geometric figures and their attributes like length, area, and volume. From mowing lawns to designing swimming pools, understanding mensuration is crucial for solving real-world problems involving shapes and spaces.

Key Concepts in Mensuration

Perimeter and Area

Before diving into complex shapes, let’s revisit some basic concepts:

• Perimeter: The distance around a figure.
• Area: The surface covered by a figure.

For example, consider a boy mowing the lawn. The area of the field he’s mowing and the perimeter of the field are key measurements he’ll need.

Similarly, the surface of the water in a swimming pool covers the area, while the border of the pool defines the perimeter. 

Formulas for Common Shapes

Rectangle and Square

• Rectangle: Area = Length × Breadth
• Square: Area = Side × Side

Triangle

• Triangle: Area = ½ × Base × Height
• Perimeter: Sum of all sides

Parallelogram

• Area: Base × Height
• Perimeter: Sum of all sides

Circle

• Area: πr² (where r is the radius)
• Circumference: 2πr

Practical Examples

Parallelogram

For a parallelogram with sides of 14 cm, 7cm, and a height of 7 cm:

• Perimeter: 2(14 + 7) = 42 cm
• Area: 14 × 7 = 98 cm²

Semi-Circle

For a semi-circle with a radius of 7 cm:

• Perimeter: πr + diameter = 22 + 14 = 36 cm
• Area: ½ × πr² = 77 cm²

Triangle

For a triangle with sides 11 cm, 10 cm, and 14 cm:

• Perimeter: 35 cm
• Area: ½ × 14 × 7 = 49 cm²

Path in a Rectangle

To find the area of a path around a rectangle:

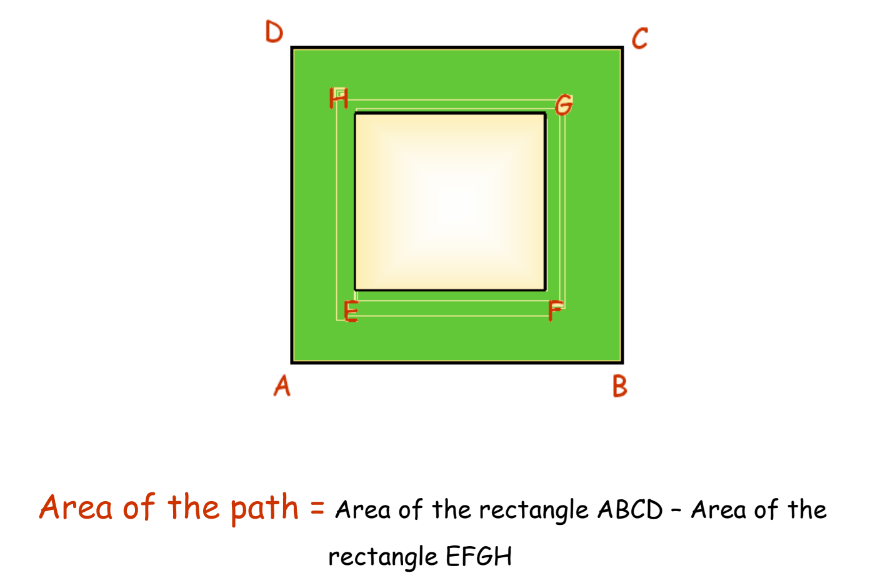
• Outer Rectangle (ABCD): 25 m × 20 m = 500 m²
• Inner Rectangle (EFGH): 21 m × 16 m = 336 m²
• Area of Path: 500 m² – 336 m² = 164 m²

Special Shapes

Trapezium

To find the area of a trapezium:

• Area: ½ × (Sum of parallel sides) × Height

Quadrilateral

To find the area of a general quadrilateral:

• Area: ½ × AC × (h1 + h2)

Rhombus

For a rhombus:

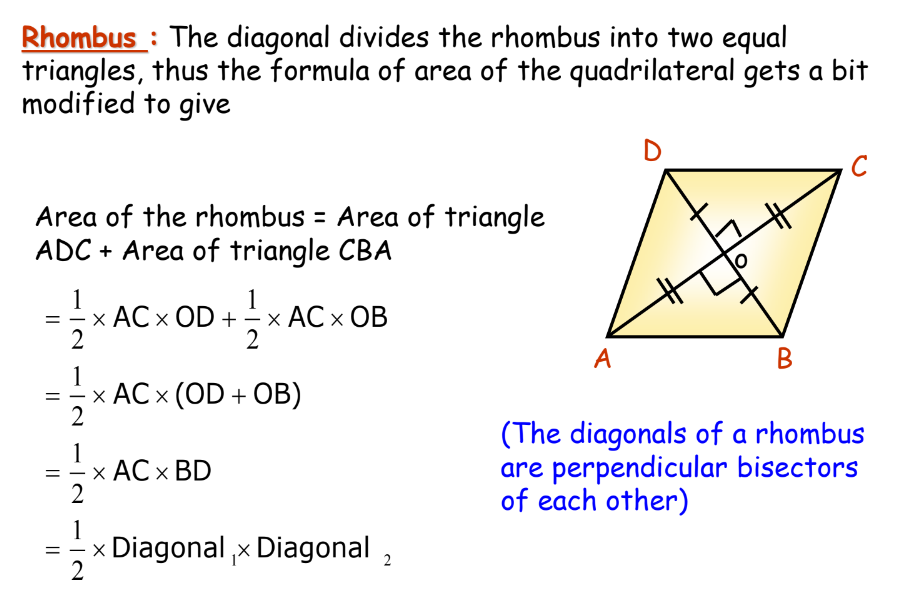
• Area: ½ × Diagonal₁ × Diagonal₂

Polygon

To find the area of a polygon:

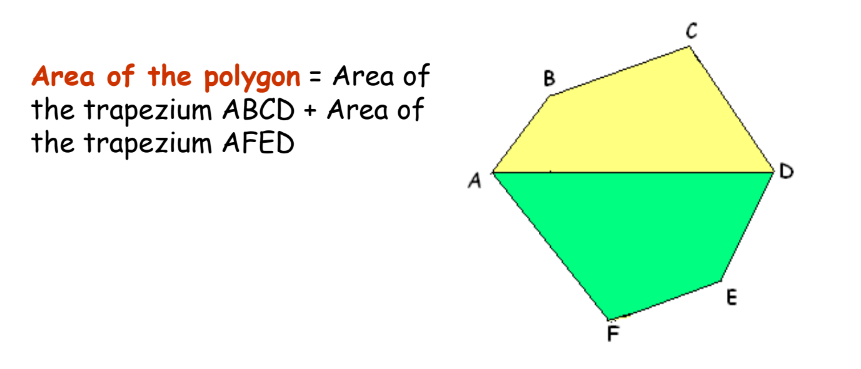
• Area: Sum of areas of triangles and trapeziums formed within the polygon

Surface Areas of 3D Figures

Cuboid and Cube

• Cuboid Total Surface Area: 2(lb + bh + hl)
• Cuboid Lateral Surface Area: 2(bh + lh)
• Cube Total Surface Area: 6a²
• Cube Lateral Surface Area: 4a²

Cylinder

• Curved Surface Area: 2πrh
• Total Surface Area: 2πr(r + h)

Volumes of 3D Shapes

Volume of Cuboid

• Volume: Length × Breadth × Height

Volume of Cube

• Volume: Side³

Volume of Cylinder

• Volume: πr²h

Practical Applications

Example: Volume of a Hollow Cylinder

For a hollow cylinder with an inner radius of 12 cm, outer radius of 14 cm, and height of 35 cm:

• Volume of Wood: πh(R² – r²) = 5720 cm²

Conclusion

Mensuration is not just a theoretical concept but a practical tool used in various fields such as architecture, engineering, and everyday life. Understanding the formulas and their applications enables us to solve real-world problems efficiently and accurately.