Circles- Complete Guide for Class 9 Math Chapter 9
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Circles in Mathematics Class 9th chapter 9 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.
Chapter 9 of Class 9 Mathematics focuses on Circles, exploring fundamental concepts such as the definition of a circle, its various components (radius, diameter, chord, secant, tangent, arc), and properties. The chapter delves into theorems related to angles subtended by chords, cyclic quadrilaterals, and tangent properties, providing a comprehensive understanding of the geometric principles and their applications.
Definition Of Circles
Circles are round objects. This chapter delves into the fundamental aspects of circles, their properties, and related theorems. For Example –

Related Terms
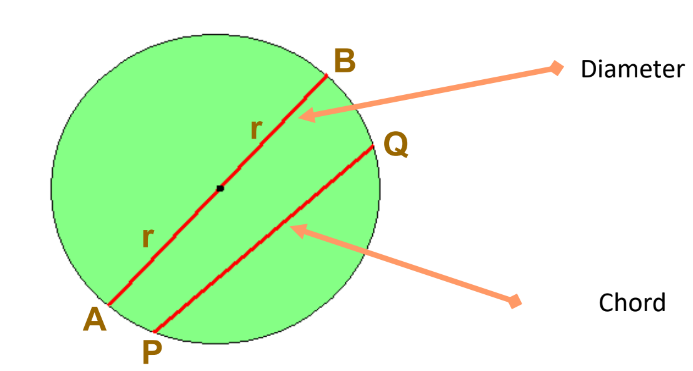
- Circle: The collection of all points in a plane that are at a fixed distance from a fixed point in the plane.
- Center: The fixed point of the circle.
- Radius: The fixed distance from the center to any point on the circle.
Diameter and Chord
- Diameter: The longest chord of a circle, equal to two times the radius.
- Chord: A line segment with both endpoints on the circle.
Arcs
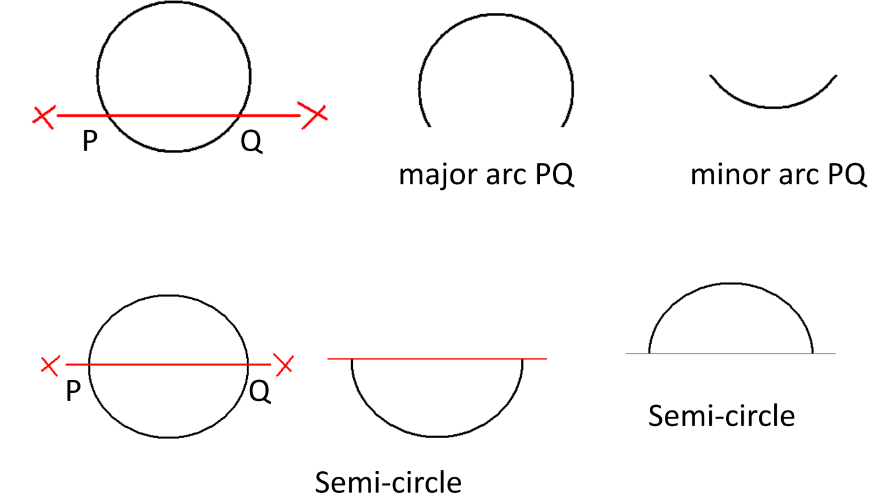
- Major Arc and Minor Arc: Different segments of a circle.
- Semi-circle: Half of a circle.
Circumference
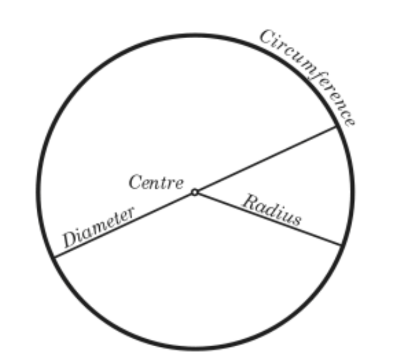
The length of the complete circle.
More Related Terms:
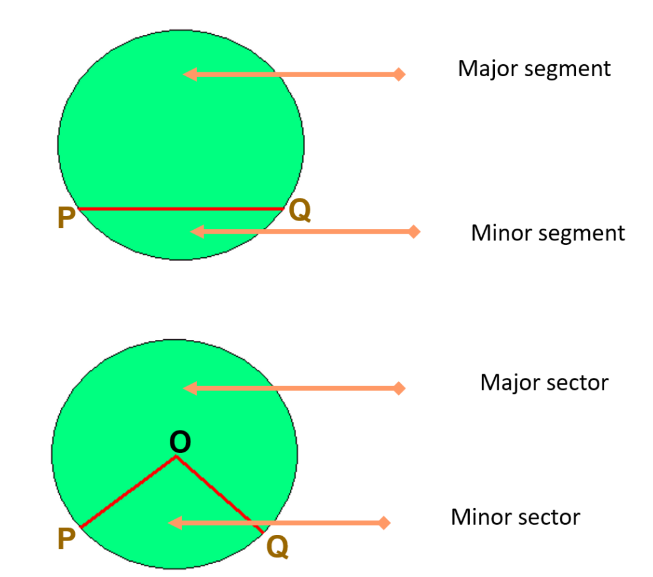
Angles Subtended by Chords
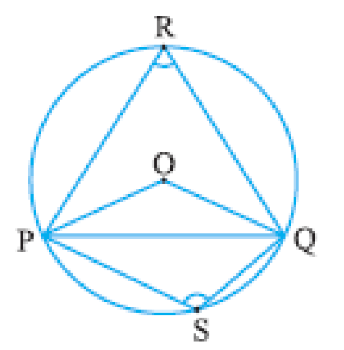
- Angles subtended by chord PQ at the center is ∠POQ.
- Angles subtended by chord PQ at the major arc is ∠PRQ.
- Angles subtended by chord PQ on the minor arc is ∠PSQ.
Theorems
- Equal Chords Subtend Equal Angles:
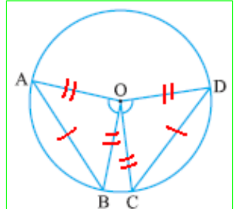
Given: AB = CD
To Prove: ∠AOB = ∠COD
Proof: In triangle AOB and COD
OA = OC (radii)
OB = OD (radii)
AB = CD (given)
⧍AOB ≅ ⧍COD (SSS)
∠AOB = ∠COD (CPCT)
- If the angles subtended by the chords at the center are equal, then the chords are equal:
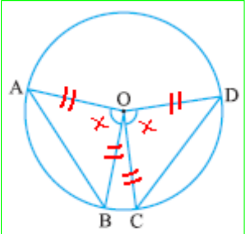
Given: ∠AOB = ∠COD
Prove: AB = CD
Proof: In triangle AOB and COD
OA = OC (radii)
OB = OD (radii)
∠AOB = ∠COD (given)
⧍AOB ≅ ⧍COD (SAS)
AB = CD (CPCT)
Perpendicular from the Centre to a Chord
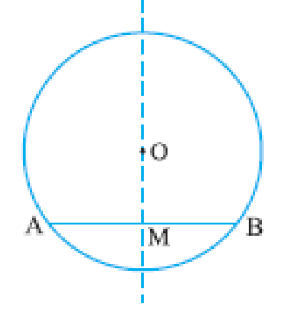
AB is the chord.
OM is the perpendicular from the center of the circle to the chord AB.
- The perpendicular from the center of a circle to a chord bisects the chord.
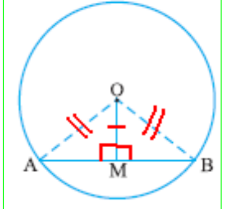
Given: OM ⊥ AB
Prove: AM = BM
Proof: In triangles OMA and OMB
OA = OB (radii)
OM = OM (common)
∠OMA = ∠OMB = 90⁰ (given)
⧍AOM ≅ ⧍BOM (RHS)
AM = BM (CPCT)
- The line drawn through the center of a circle to bisect a chord is perpendicular to the chord:
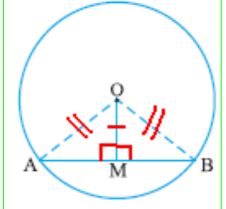
Given: AM = BM
Prove: OM ⊥ AB
Proof: In triangles OMA and OMB.
OA = OB (radii)
OM = OM (common)
AM = BM (given)
⧍AOM ≅ ⧍BOM (SSS)
∠OMA = ∠OMB = 90⁰ (CPCT)
Circles Through Points
- Infinite circles can pass through one or two points.
- Only one circle can pass through three non-collinear points.
- There is one and only one circle passing through three given non-collinear points.
If ABC is a triangle.
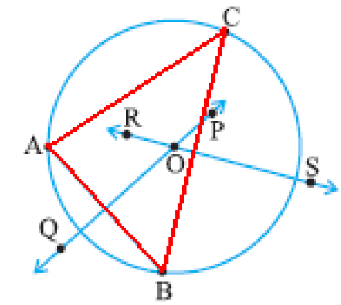
• Then the circle (above) is called the circumcircle.
• Centre of the circle is called the circumcentre.
• Radius of the circle is called circumradius.
Equal Chords and Distances from Centre
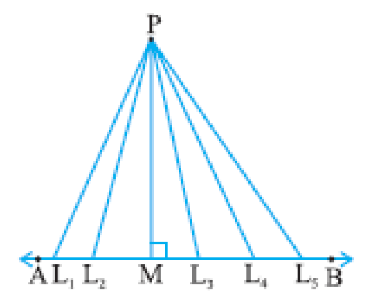
The length of the perpendicular from a point to a line is the distance of the line from the point.
In the figure above, PM is the distance of the line AB from the point.
Equal Chords and Distances
- Theorem: Equal chords are equidistant from the center.
- Theorem: Chords equidistant from the center are equal.
Angles Subtended by Arcs
- Theorem: Equal chords have congruent arcs and subtend equal angles at the center.
- Theorem: The angle subtended by an arc at the center is double the angle subtended at any other point.
Cyclic Quadrilaterals
- Definition: A quadrilateral with all vertices on a circle.
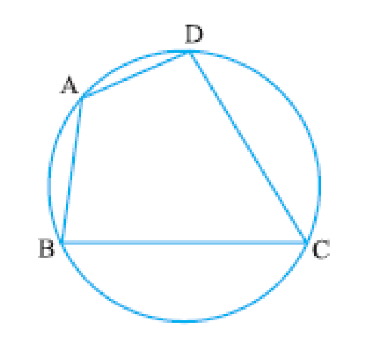
- Theorem: The sum of either pair of opposite angles of a cyclic quadrilateral is 180⁰.
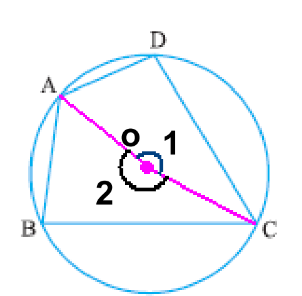
Draw AO & OC and name the angles as ∠1 and ∠2 as shown in the figure.
∠1 = 2 ∠ABC
∠2 = 2 ∠ADC
∠1 + ∠2 = 2 ( ∠ABC + ∠ADC)
But, ∠1 + ∠2 = 360⁰
2 ( ∠ABC + ∠ADC) = 360⁰
and ( ∠ABC + ∠ADC) = 180⁰
By understanding these fundamental properties and theorems, students will gain a comprehensive understanding of circles for chapter,9 class 9, and their geometric significance.
In conclusion, Chapter 9 of Class 9 Mathematics, Circles, offers a deep dive into one of the most fascinating geometric shapes. From understanding the basic definition of a circle to exploring its components like radius, diameter, and chords, to learning essential theorems, this chapter lays a solid foundation in geometry.
The practice of these concepts will enable you to solve complex problems with ease. At iPrep, our resources for Class 9 Math Chapter 9 Circles are tailored to ensure you excel in your studies. Dive into the animated videos, practice exercises, and notes to reinforce your understanding of Circles and boost your performance in exams. Keep revisiting this guide to master the intricacies of Class 9 Chapter 9 Circles, and enjoy learning with iPrep!
Practice questions on Chapter 9 - Circles
Get your free Chapter 9 - Circles practice quiz of 20+ questions & detailed solutions
Practice Now








