Complete Guide For Class 9 Math Chapter 8 – Quadrilaterals

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Quadrilaterals in Mathematics Class 9th Chapter 8 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

Chapter 8 introduces four-sided polygons. It covers types of quadrilaterals (parallelogram, rectangle, square, rhombus, trapezium), their properties, and conditions for specific quadrilaterals. Key concepts include angle sum property, properties of diagonals, and relationships between sides and angles.

Quadrilaterals

A quadrilateral is a figure formed by joining four points in an order. Understanding its types, properties, and related theorems is fundamental in geometry.

Types of Quadrilaterals

• Regular Quadrilaterals:

1. Parallelogram
2. Kite
3. Trapezium

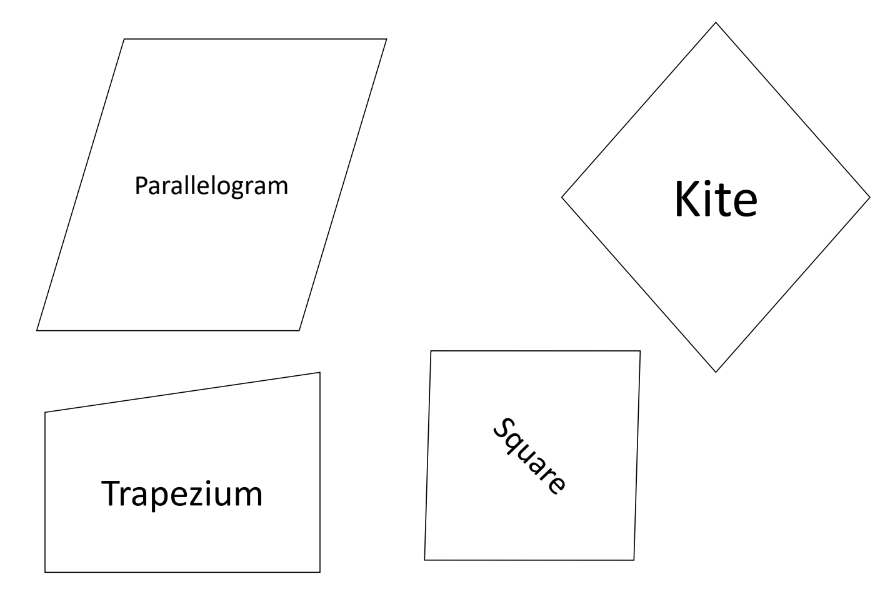
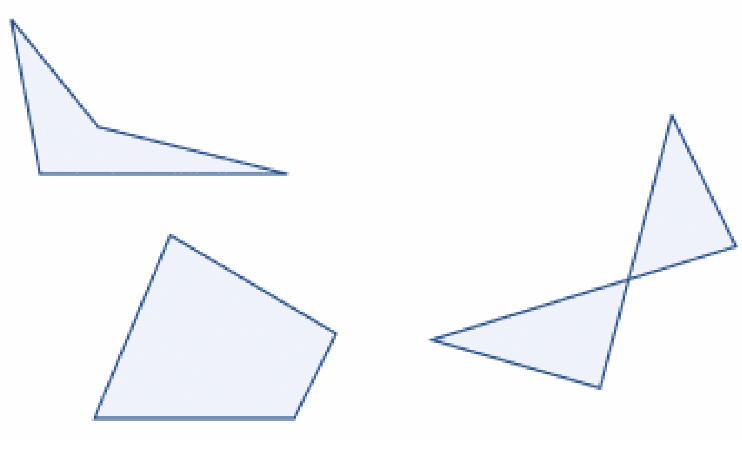
• Irregular Quadrilaterals:

1. Quadrilaterals that do not fit into the categories of regular quadrilaterals.

Angle Sum Property of a Quadrilateral

The sum of the angles of a quadrilateral is 360º. This can be verified by dividing the quadrilateral into two triangles using a diagonal.

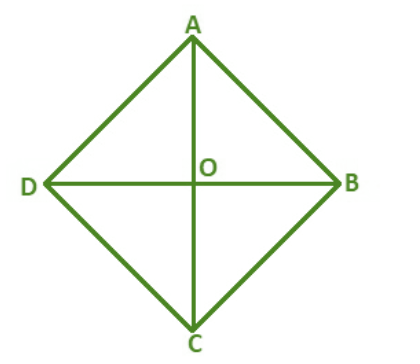
Proof:

Let ABCD be a quadrilateral with AC as a diagonal.

In triangle ΔDAC: ∠DAC + ∠ACD + ∠D = 180°

In triangle ΔCAB: ∠CAB + ∠ACB + ∠B = 180°

Adding these, we get ∠DAC + ∠ACD + ∠D + ∠CAB + ∠ACB + ∠B = 360°

Thus, ∠A + ∠B + ∠C + ∠D = 360°

Example: If three angles of a quadrilateral are 110°, 50°, and 40°, find the fourth angle: 

Solution: 110° + 50° + 40° + x = 360° x = 160°.

Parallelogram

A parallelogram is a quadrilateral with two sets of parallel sides. Key properties include:

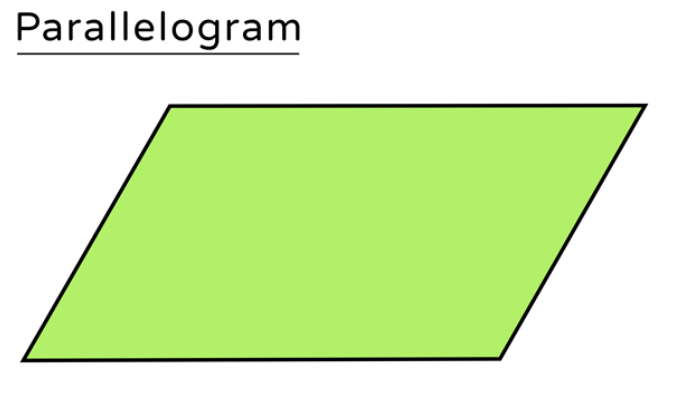
1. Opposite sides are equal.
2. Opposite angles are congruent.
3. Diagonals bisect each other.

Theorems Related to Parallelograms

Theorem 1: A diagonal of a parallelogram divides it into two congruent triangles.

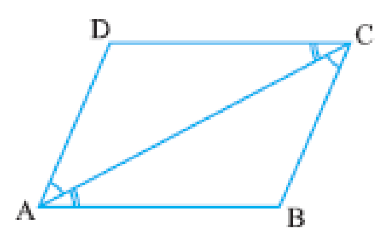
• Proof: Let ABCD be a parallelogram and AC be a diagonal. Observe that the diagonal AC divides parallelogram ABCD into two triangles, namely, Δ ABC and Δ CDA. We need to prove that these triangles are congruent.

In Δ ABC and Δ CDA, BC || AD and AC is a transversal. So, ∠ BCA = ∠ DAC (Pair of alternate angles). Also, AB || DC and AC are transversals. So, ∠ BAC = ∠ DCA (Pair of alternate angles) and AC = CA (Common)

So, Δ ABC ≅ Δ CDA (ASA rule) or, diagonal AC divides parallelogram ABCD into two congruent triangles ABC and CDA. Thus, AB = DC and AD = BC.

Hence Proved.

Theorem 2: In a parallelogram, opposite sides are equal.

• Proof: Since we have already proved that a diagonal divides the parallelogram into two congruent triangles. The congruent parts of congruent triangles are equal. Thus, AB = DC and AD = BC.

Theorem 3: The opposite angles of a parallelogram are equal.

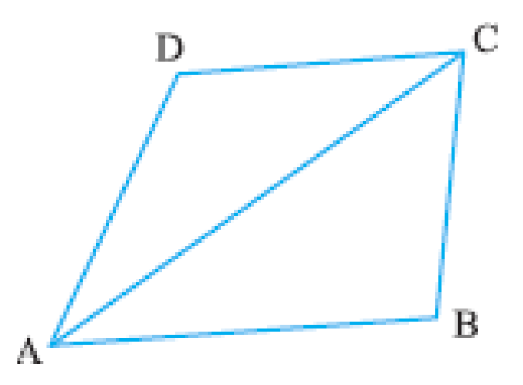
• Proof: Given: A parallelogram ABCD

To prove:  ∠ A = ∠ C and  ∠ B = ∠ D

Proof: Since ABCD is a parallelogram, Therefore,

AB ∥ DC and AD ∥ BC

Now, AB∥ DC and transversal AD intersects them at A and D respectively.

 ∠ A + ∠D = 180° and  ∠ D + ∠ C = 180°

 ∠ A + ∠D = ∠ D + ∠ C

So,  ∠ A = ∠ C

Similarly, ∠ B = ∠ D

Hence,  ∠ A = ∠ C and ∠ B = ∠ D

Theorem 4: The diagonals of a parallelogram bisect each other.

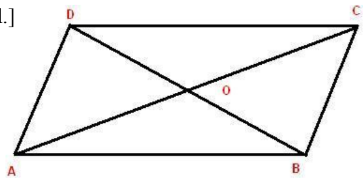
• Proof: Given: A parallelogram ABCD such that its diagonals AC and BD intersect at O.

To Prove: OA = OC and OB = OD

Proof : Since, ABCD is a parallelogram. Therefore,

AB ∥ DC and AD ∥ BC

Now, AB ∥ DC and transversal AC intersects them at A and C respectively.

∠BAC = ∠DCA (Since alternate interior angles are equal.) 

∠BAO = ∠DCA  (i)

Again, AB ∥ DC and transversal BD intersect them at B and D respectively.

 ∠ABD = ∠CDB (Since alternate interior angles are equal.) 

∠ABO = ∠CDO  (ii)

Now, in triangles, AOB, and COD, we have

∠BAO = ∠DCO [from (i)]

AB = CD [ Opposite sides of a parallelogram are equal.]

and,  ∠ABO = ∠CDO [from (ii)]

So, by ASA congruence criterion 

⧍ABO ≅ ⧍COD

OA = OC and OB = OD [c.p.c.t.]

Hence, OA = OC and OB = OD

Properties of Rectangle, Rhombus, and Square

Rectangle

1. Each angle is a right angle.
2. Diagonals are equal in length.

Rhombus:

1. All sides are of equal length.
2. Opposite angles are equal.

Square:

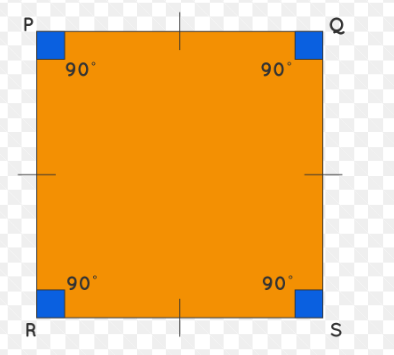
1. All angles are right angles.
2. All sides are of equal length.

Some Useful Facts About a Triangle

Theorem 1: The line segment joining the mid-points of two sides of a triangle is parallel to the third side.

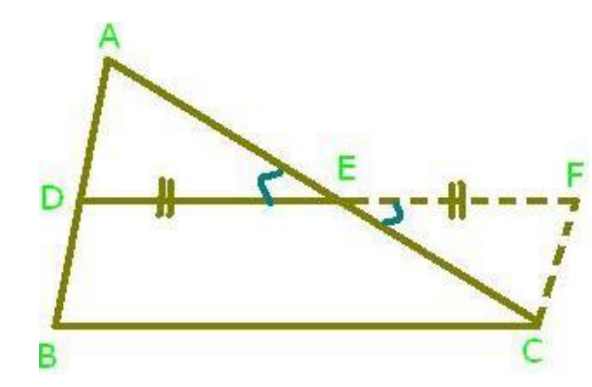
• Proof: Given: A  ⧍ABC in which D and E are the midpoints of sides AB and AC respectively. DE is joined.

To prove: DE ∥ BC and DE = 1/2 BC

Construction: Produce the line segment DE to F, such that DE = EF. Join FC

Proof: In triangles AED and CEF, we have 

AE = CF [ E is the midpoint of AC]

∠AED = ∠CFE [Vertically Opposite angles]

and, DE = EF [By construction]

So, by the SAS congruence criterion, we have

⧍ABO ≅ ⧍COD

AD = CF [c.p.c.t] ……..(i)

and, ∠ADE = ∠CFE……..(ii)

Now, D is the midpoint of AB

AD = DB

DB = CF ………(iii)

Now, DF intersects AD and FC at D and F respectively such that

∠ADE = ∠CFE……..from (ii)

i.e., alternate interior angles are equal.

AD ∥ FC 

DB  ∥ CF

From (iii) and (iv), we find that DBCF is a quadrilateral such that one pair of sides is equal and parallel.

Therefore, DBCF is a parallelogram

DF  ∥ BC and DF = BC [opposite sides of a parallelogram are equal and parallel]

But D, E, and F are collinear, and DE = EF.

Therefore, DE  ∥ BC and DE = 1/2 BC 

Theorem 2: The line drawn through the mid-points of one side of a triangle, parallel to another side, intersects the third side at its mid-point.

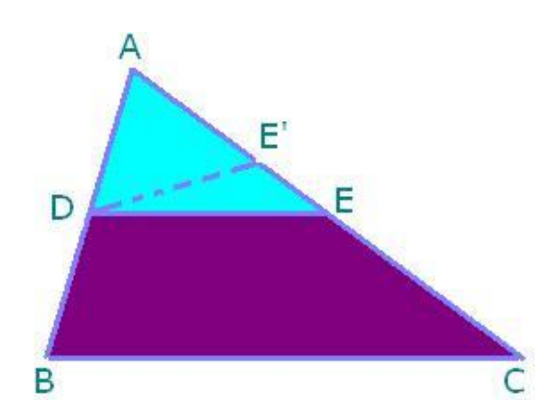
• Proof: Given: Triangle ABC in which D is the midpoint of AB and DE  ∥ BC

To prove: E is the midpoint of AC.

Proof: We have to prove that E is the midpoint of AC. If possible, let E be not the midpoint of AC. Let E prime be the midpoint of AC. Join DE Prime.

Now, in triangle ABC, D is the midpoint of AC

Therefore, we have DE’ ∥ BC….(i)

Also, DE ∥ BC….(ii)

From (i) and (ii), we find that two intersecting lines DE and DE’ are both parallel to line BC.

This is a contradiction to the parallel line axiom. So, our supposition is wrong.

Hence, E is the midpoint of AC.

Understanding these concepts and theorems about quadrilaterals is essential for mastering geometry in Class 9 mathematics. Keep practicing with examples and proofs to solidify your knowledge.

In conclusion, mastering Quadrilaterals, as covered in Class 9 Math Chapter 8 – Quadrilaterals, is essential for building a solid foundation in geometry. This chapter not only introduces you to the various types of quadrilaterals, like parallelograms, rectangles, rhombuses, and squares, but also helps you understand their unique properties and theorems. As you practice and apply these concepts, you’ll gain confidence in solving complex problems related to quadrilaterals. With iPrep’s engaging resources, including videos, notes, and practice questions, excelling in Class 9 Chapter 8 – Quadrilaterals becomes more achievable. Keep exploring and practicing to master quadrilaterals and enhance your overall understanding of geometry!