Introduction to Euclid’s Geometry- Complete Guide For Class 9 Math Chapter 5
Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Introduction to Euclid’s Geometry in Mathematics Class 9th chapter 5 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.
Chapter 5, “Introduction to Euclid’s Geometry,” for Class 9 explores the foundational principles of geometry, introduced by the ancient mathematician Euclid. This chapter covers Euclid’s definitions, axioms, and postulates, establishing a logical framework for geometric concepts. It emphasizes the importance of logical reasoning and proof in geometry, laying the groundwork for further studies in the subject.
Meaning of Geometry
The term “geometry” derives from the Greek words ‘geo,’ meaning Earth, and ‘metry,’ meaning measurement. Essentially, geometry is the measurement of the Earth.
Examples of Geometrical Figures
Ancient structures like altars (vedis), pyramids, and designs such as Sriyantra and Havan Kund illustrate early uses of geometric principles.

Euclid: The Father of Geometry
Euclid was a pioneering Greek mathematician who introduced a systematic approach to proving geometric results using deductive reasoning. This method relied on previously established results and axioms, fundamental assumptions taken as self-evident.

Thales and Pythagoras
Thales, another Greek mathematician, provided the first known geometric proof that a circle is bisected by its diameter. Pythagoras and his disciples expanded on these principles, contributing significantly to the field of geometry.
Euclid’s Contributions
Euclid compiled all known geometric knowledge into his treatise, laying the foundation for what is now known as Euclidean geometry. This geometry is based on deductive logic, emphasizing the logical structure of proofs.
Now we will learn some illustrations of Axioms for chapter 5 of class 9 “Introduction to Euclid’s Geometry”
Axioms: The basic facts that are taken for granted, without proof, are called axioms.
Illustration 1: Halves of equals are also equal
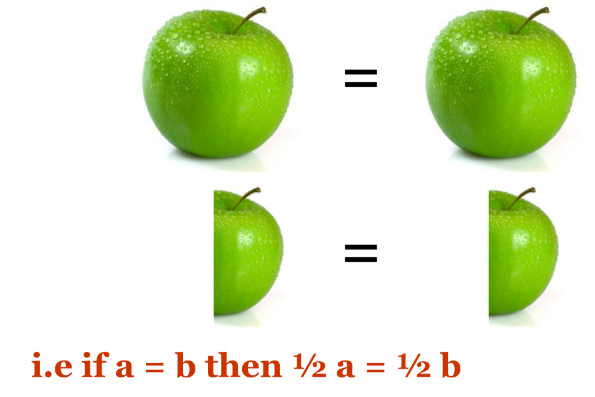
Illustration 2 :

Thus if a > b and b> c then this implies a > c.
Illustration 3: The whole is equal to the sum of the parts and greater than any of its parts.
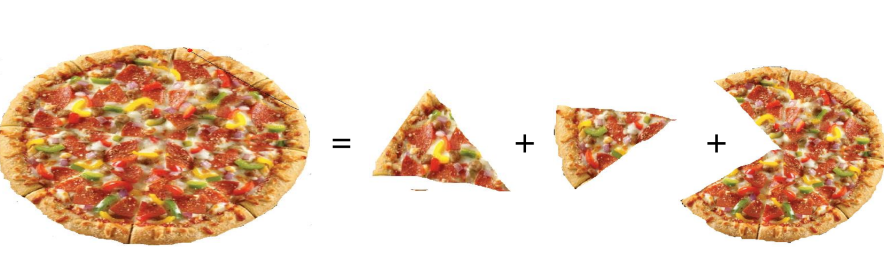
Basic Concepts in Euclid’s Geometry
Point
A point is a precise location with no length, breadth, or height, represented by a dot.
Plane
A plane is a flat, two-dimensional surface extending infinitely in all directions, like a sheet of paper or a smooth wall.
Line
A line is a collection of points extending infinitely in both directions without any endpoints.
Incidence Properties of a point
- Point Properties
a) Infinite lines can pass through a single point.
b) Only one line can pass through any two distinct points.
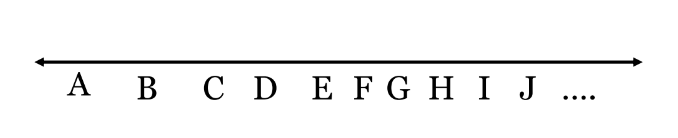
- Line Properties
Two lines can be:
a) Intersecting lines: Suppose they intersect then they have one point in common.
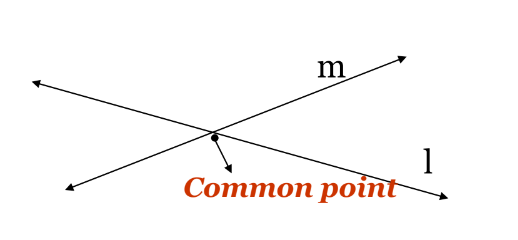
b) parallel lines: Suppose they are parallel then they have no points in common.
Axioms and Theorems
- Axioms
- Halves of equals are equal.
- The whole is greater than any of its parts.
- Theorems
- Two distinct lines cannot share more than one point.
- Lines parallel to the same line are parallel to each other.
- If a line intersects one of two parallel lines, it will also intersect the other.
Euclid’s Axioms and Postulates
Axioms
- Things equal to the same thing are equal.
- The whole is greater than the part.
Postulates
- A straight line can be drawn from any point to any other point.
- A terminated line can be extended indefinitely.
- A circle can be drawn with any center and radius.
- All right angles are equal.
- If a line intersects two others and makes the interior angles on one side less than two right angles, the two lines will eventually intersect on that side.
Equivalent Versions of Euclid’s Fifth Postulate
‘For every line l and for every point P not lying on l, there exists a unique line m passing through P and parallel to l.’
Let us understand the concept with the help of figure:
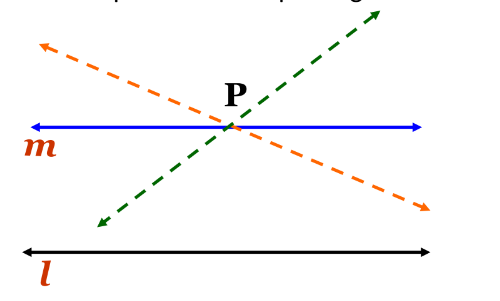
This result can also be stated in the following form: Two distinct lines cannot be parallel to the same line.
This blog post provides an overview of the foundational concepts of Euclidean geometry, highlighting the key contributions of Euclid and other early mathematicians. It serves as an introduction to the logical structure and principles that form the basis of geometric study.
In conclusion, Chapter 5: Introduction to Euclid’s Geometry is a critical foundation for understanding the logical principles behind geometry. Euclid’s contributions, along with the axioms and postulates introduced in this chapter, provide the framework for logical reasoning in mathematics. As you delve into Chapter 5: Introduction to Euclid’s Geometry, you’ll explore the timeless concepts that have shaped geometry as we know it today. The understanding of basic geometrical terms like points, lines, and planes, along with the significant role of Euclid’s axioms and postulates, lays the groundwork for more advanced studies. Remember, Chapter 5: Introduction to Euclid’s Geometry isn’t just about memorizing definitions; it’s about developing a methodical approach to solving problems through logical reasoning. As you continue, the knowledge gained in Chapter 5: Introduction to Euclid’s Geometry will serve as a strong foundation for all future geometrical concepts.
Practice questions on Chapter 5 - Introduction to Euclid's Geometry
Get your free Chapter 5 - Introduction to Euclid's Geometry practice quiz of 20+ questions & detailed solutions
Practice Now








