Surface Areas and Volumes- Complete Guide For Class 9 Math Chapter 11
Our learning resources for Mathematics Class 9 ‘Surface Areas and Volumes’ chapter 11 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions, and notes offer you the best of integrated learning with interesting explanations and examples.
Our comprehensive approach ensures that you have access to everything you need to have an in-depth understanding of the chapter Surface Areas and Volumes. From detailed notes to interactive exercises, our materials are tailored to meet your learning needs and help you excel in your studies. Get ready to dive into an enriching educational experience that will make mastering this chapter a breeze.
Chapter 11, “Surface Area and Volume,” introduces students to calculate the surface area and volume of various 3D shapes, including cubes, cuboids, cylinders, cones, spheres, and hemispheres. It covers the derivation of formulas and practical applications. Emphasis is on understanding and applying these formulas to solve real-world problems, enhancing spatial reasoning and mathematical modeling skills.
Welcome to the fascinating world of 3-dimensional geometry! In this chapter, we explore solid figures, including cuboids, cubes, cylinders, cones, and spheres, learning how to calculate their surface areas and volumes. By mastering these concepts, you’ll be able to solve real-life problems involving various geometrical shapes.
Introduction to Solid Figures
Until now, we have focused on plane figures like circles, squares, and rectangles. Now, we shift our attention to solid figures, which have three dimensions. Examples include cuboids, cubes, and cylinders. Let’s delve into the formulas for their surface areas and volumes.
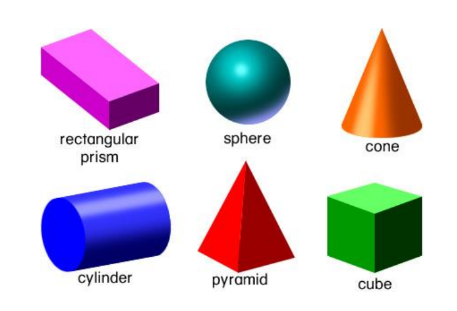
Surface Area of Cuboids and Cubes
Cuboid: A solid figure bounded by six rectangular plane regions.

- Faces: Six rectangular faces.
- Edges: Twelve edges where adjacent faces meet.
- Lateral Faces: Four faces that meet the base of the cuboid.
Total Surface Area of a Cuboid: TSA = 2(lb+bh+lh)
Lateral Surface Area of a Cuboid: LSA = 2(l+b)h
Cube: A cuboid with equal length, breadth, and height.
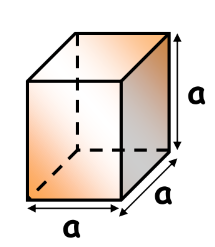
Total Surface Area of a Cube: TSA = 6a²
Lateral Surface Area of a Cube: LSA = 4a²
Examples
- Cuboid Tiffin Box: Find the surface area for dimensions 16 cm x 8 cm x 6 cm.

Solution: TSA = 2(16×8+8×6+6×16) = 2 ×272 = 544 cm²
- Dimensions Ratio: A cuboid with a surface area of 88 m² and dimensions in a 1:2:3 ratio. Find the dimensions of the cuboid.
Solution: The length, breadth, and height are l, 2l, and 3l respectively.
Then T.S.A of the cuboid = 2(lb+bh+hl)
88 = 2(lx2l + 2lx3l + lx3l)
88 = 2(2l² + 6l² + 3l²)
l² = 4
l = 2
Thus the dimensions are 2m, 4m, 6m.
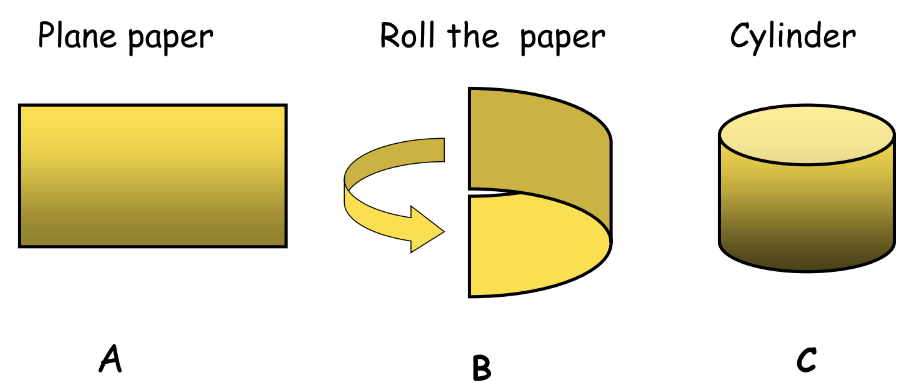
Cylinder
A cylinder is formed by rolling a rectangular sheet.
Curved Surface Area (CSA): CSA = 2πrh
Total Surface Area: TSA = 2πr(r+h)
Examples
- Rectangular Sheet to Cylinder: A rectangular sheet of paper 44 cm x 18 cm is rolled along its length and a cylinder is formed. Find the radius of the cylinder.
Solution: The length of the rectangular sheet forms the circumference of the base, and the breadth becomes the height of the cylinder.
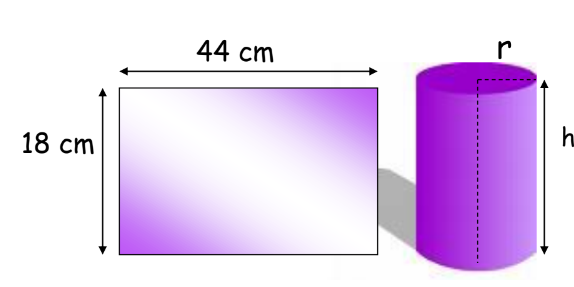
2πr = 44
2 × 22/7 × r = 44
r = 44 × 7 /2 × 22 = 7 cm
- Hot Water Heating System: In a hot water heating system, there is a cylindrical pipe of length 28 m and the diameter is 5 cm. Find the total radiating surface in the system.
Solution: The total radiating surface = 2πrh
Length = height = 28 m
radius = 5 cm = 5/200 m
Therefore the curved surface area = 2 × 22/7 × 5/200 × 28 = 4.4 m²
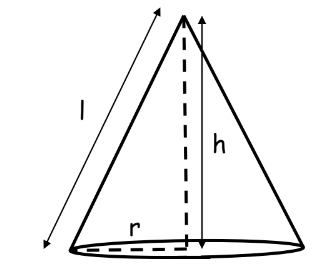
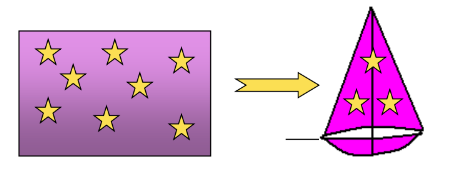
Cones
A cone is formed by rotating a right-angled triangle around one of its legs.

Curved Surface Area: CSA = πrl
Total Surface Area: TSA = πr(l+r)
Examples
- Curved Surface Area: The radius of a cone is 3 cm and its vertical height is 4 cm. Find the area of its curved surface.
Solution: We have radius = 3 cm and h = 4 cm . Let l be the slant height of the cone
l ² = r² + h²
l² = 3² + 4²
l² = 9 + 16
l² = 25
l = 5
Therefore Curved surface area = πrl = 22/7 × 3 ×4 = 141.3 cm²
- Cloth for Conical Tent: How many meters of cloth 5 m wide will be required to make a conical tent, the radius of whose base is 7 m and whose height is 24 m?
Solution: According to the question
l² = r² + h²
l² = 7² + 24²
l² = 49 + 576
l² = 625
l = 5
Area of the cloth = Curved surface area of the tent
l × b = πrl
l × 5 = 22/7 × 7 × 25
l = 110m
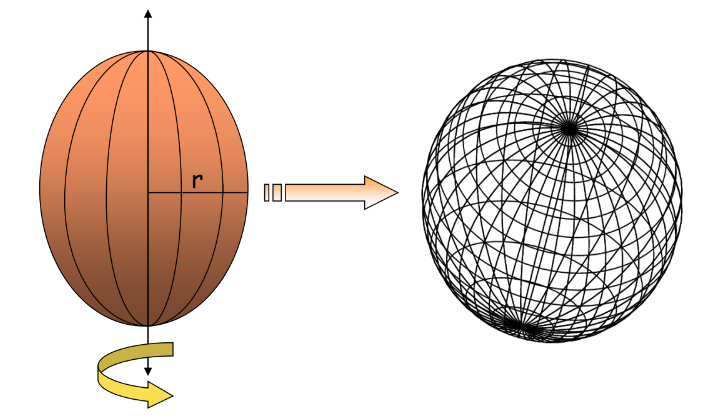
Spheres and Hemispheres
Sphere Surface Area: SA = 4πr²
Hemisphere Curved Surface Area: CSA = 2πr²
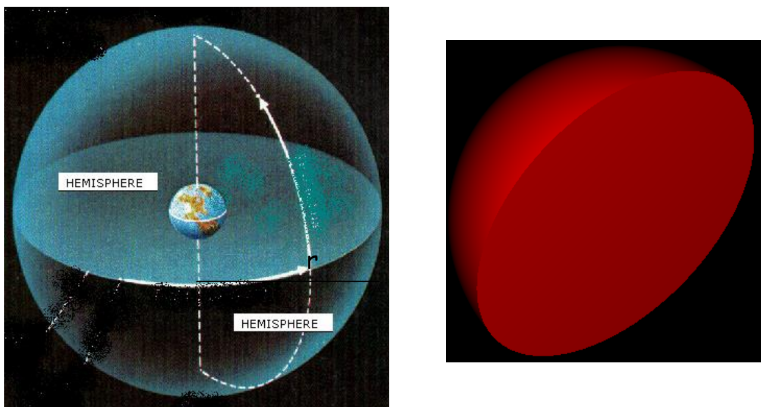
Total Surface Area of Hemisphere: TSA = 3πr²
Volumes of Solid Shapes
The space occupied by a solid object is its volume. For hollow objects, the capacity is measured.

Cuboid and Cube
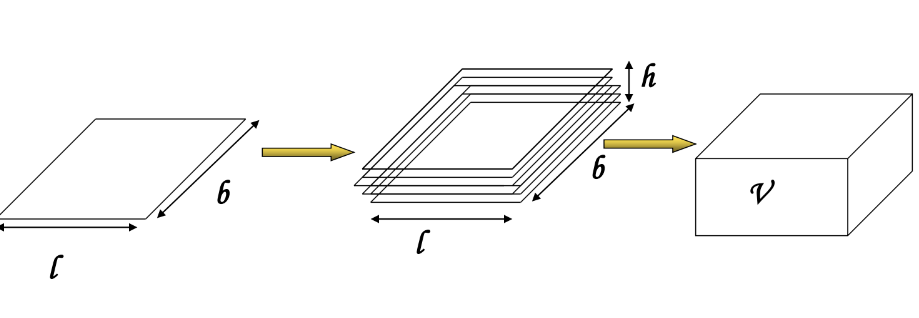
Volume of a Cuboid: V = l × b × h
Volume of a Cube: V = a³
Cylinders
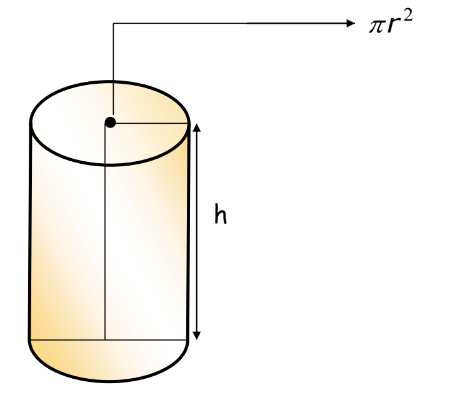
Volume of a Cylinder: V = πr²h
Hollow Cylinder: V = πh(R²−r²)
Cones
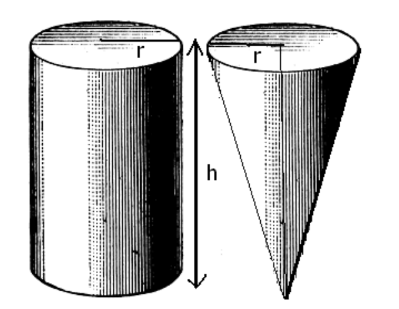
Volume of a Cone: V = 1/3πr²h
Suppose there is a cone and a cylinder of the same height and the same radius.
The volume of the cone = 1/3 × Volume of the cylinder
V = 1/3πr²h
Sphere and Hemisphere
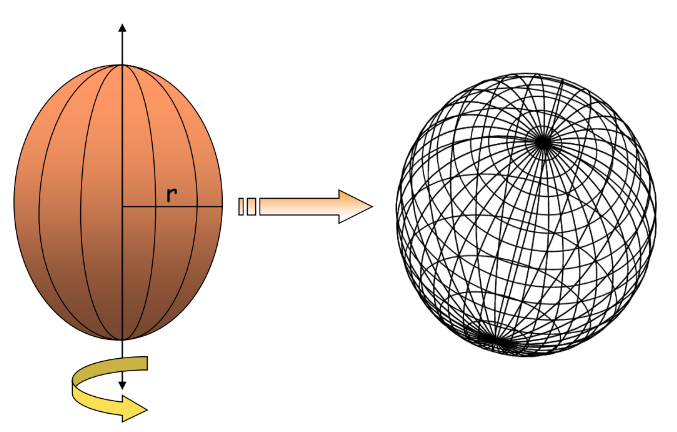
Volume of Sphere = 4/3 × πr³
Volume of Hemisphere = 2/3 × πr³
Understanding surface areas and volumes is crucial for solving practical problems involving three-dimensional shapes. By mastering these formulas and concepts, students can effectively tackle various geometrical challenges.
In conclusion, Chapter 11 – Surface Areas and Volumes of Class 9 Mathematics provides a thorough exploration of three-dimensional geometry. By understanding the key concepts and formulas for calculating the surface areas and volumes of various solid figures such as cuboids, cubes, cylinders, cones, spheres, and hemispheres, students gain valuable skills applicable to both academic and real-world scenarios.
Our resources for Surface Areas and Volumes ensure a comprehensive learning experience. With engaging animated videos, detailed notes, and practice questions, you will be well-equipped to master this chapter with ease. Whether you’re preparing for exams or seeking to reinforce your understanding, our materials are designed to enhance your grasp of Surface Areas and Volumes and help you excel in your studies.
By delving into the principles of Surface Areas and Volumes, you will improve your spatial reasoning and problem-solving abilities. Remember, mastering these concepts opens doors to tackling more complex geometrical problems, making your mathematical journey both enriching and rewarding. So, embrace the challenge and enjoy the learning process as you explore the fascinating world of Surface Areas and Volumes.
Practice questions on Chapter 11 - Surface Areas And Volumes
Get your free Chapter 11 - Surface Areas And Volumes practice quiz of 20+ questions & detailed solutions
Practice Now








