Complete Guide For Class 9 Math Chapter 7 – Triangles

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Triangles in Mathematics Class 9th chapter 7 are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples.

This chapter focuses on the properties of triangles. It covers the congruence of triangles (SSS, SAS, ASA, RHS criteria), inequalities in triangles, and the relationship between sides and angles. Key concepts include isosceles and equilateral triangles and the exterior angle property.

Triangles

A triangle is a closed figure made up of three line segments. A triangle has:

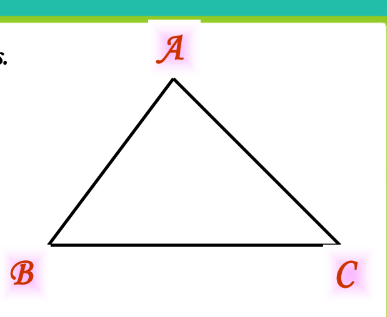
• 3 sides: AB, BC, CA
• 3 angles: ∠ABC, ∠BCA, ∠CAB
• 3 vertices: A, B, C

Concept of Congruence

Congruence means that when one figure completely overlaps another, the objects are equal in all respects; the shapes and sizes of the figures are the same. Congruent figures include circles, stars, cubes, and hexagons.

Non-Congruent Figures

When one figure completely overlaps the other figure, the objects are equal in all respects, and the shapes and sizes of the figures are the same. Then the objects are said to be congruent.

Though they may be similar, concentric circles and cylinders are examples of figures that are similar but not congruent.

Congruent Triangles

Given triangles with sides and angles as specified:

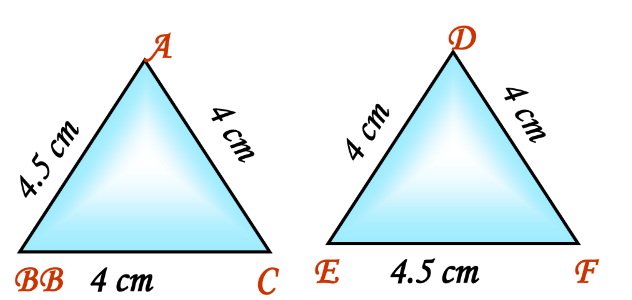
Example:

• AB = EF
• BC = FD
• CA = DE

Criteria for Congruence of Triangles

SAS Congruence Condition

Two triangles are congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.

ASA Congruence Rule

Theorem: If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the two triangles are congruent.

Proof:

• Case 1:

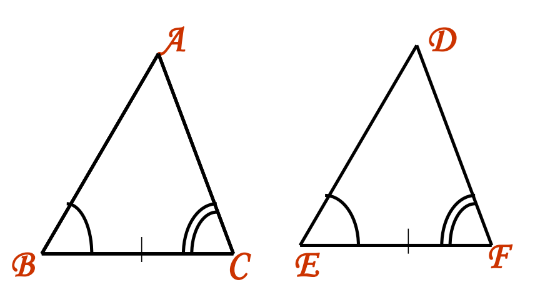
Suppose, AB = DE

∠B = ∠E

BC = EF

Therefore, ΔABC ≅ ΔDEF

• Case 2: When AB > ED:

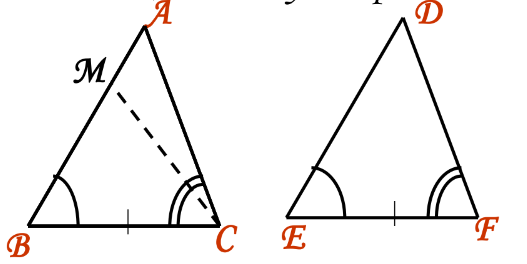
There may be a point M on AB where MB = DE, ∠B = ∠E, and BC = EF.

Therefore, ΔABC ≅ ΔDEF.

• Case 3: When AB < ED:

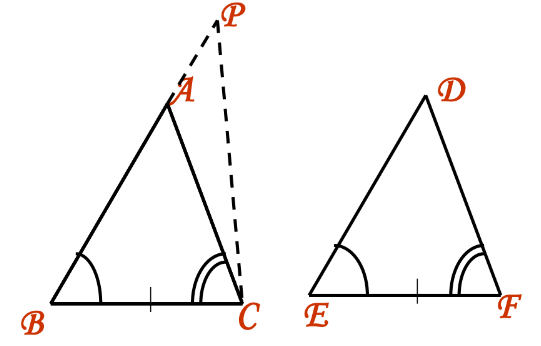
There exists a point P on AB where BP = ED, ∠B = ∠E, and BC = EF.

Therefore, ΔABC ≅ ΔDEF.

Applications Based on SAS and ASA Congruence

Example 1: In Quadrilateral ABCD, AC bisects ∠A and side AB = AD. Show that ΔADC ≅ ΔABC.

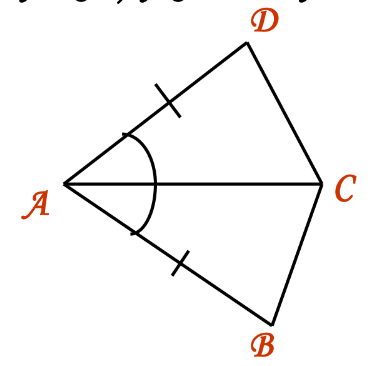
Solution: In ΔADC and ΔABC:

• AD = AB (Given)
• AC = AC (Common)
• ∠DAC = ∠BAC (Since AC is the angle bisector)
• By SAS rule, ΔADC ≅ ΔABC.

Example 2: Given Quadrilateral ABCD with AB = DC, and ∠DAB = ∠ADC. Show that ΔADC ≅ ΔDAB.

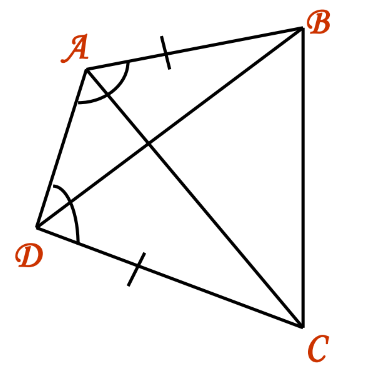
Solution: In ΔADC and ΔDAB:

• ∠ADC = ∠DAB
• AD = AD (Common)
• AB = DC (Given)
• By SAS rule, ΔADC ≅ ΔDAB.

Some Properties of a Triangle

Isosceles Triangle

A triangle in which two sides are equal.

Example: In triangle ABC, AB = AC.

Theorem: Angles opposite to equal sides of an isosceles triangle are equal. 

Proof: Construct the angle bisector of ∠A. In ΔABD and ΔACD:

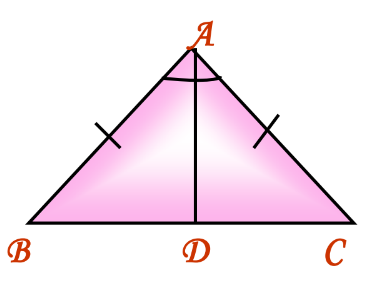
• AB = AC (Equal sides)
• ∠BAD = ∠CAD (AD is the angle bisector)
• AD = AD (Common)
• By the SAS rule, ΔABD ≅ ΔACD, thus ∠ABD = ∠ACD.

Theorem: The sides opposite to equal angles of a triangle are equal. 

Proof: Construct the perpendicular bisector AD to side BC. In ΔABD and ΔACD:

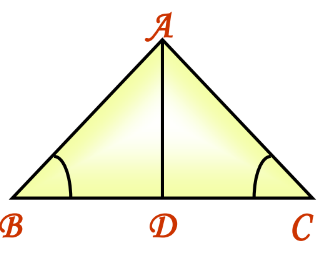
• AD = AD (Common)
• ∠ABD = ∠ACD
• ∠ADB = ∠ADC (AD is the perpendicular bisector)
• By AAS rule, ΔABD ≅ ΔACD, thus AB = AC.

Applications Based on Isosceles Triangle

Example 1: In isosceles triangle ABC with AB = AC, bisectors of ∠B and ∠C intersect at O.

Solution: In ΔAOB and ΔAOC:

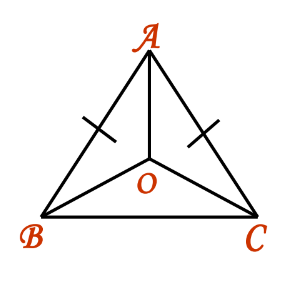
• AB = AC (Given)
• OB = OC (Proved)
• OA = OA (Common)
• By SSS rule, ΔAOB ≅ ΔAOC, thus AO bisects ∠A.

Example 2: In isosceles triangle ABC with altitudes BE and CF drawn to equal sides AC and AB respectively.

Solution: In ΔBEC and ΔCFB:

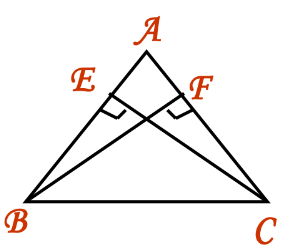
• ∠B = ∠C (Angles opposite to equal sides)
• BC = BC (Common)
• ∠E = ∠F (Right angles)
• By the AAS rule, ΔBEC ≅ ΔCFB, thus BE = CF.

Some More Criteria for Congruence of Triangles

RHS Congruence Criterion

Theorem: Two right triangles are congruent if the hypotenuse and one side of one triangle are respectively equal to the hypotenuse and one side of the other triangle.

SSS Congruence Rule

If the three sides of one triangle are equal to the three sides of another triangle, then the two triangles are congruent.

Applications Based on Congruence

Example: AD is an altitude of an isosceles triangle ABC in which AB= AC, showing that (i) AD bisects BC (ii) AD bisects ∠A

Solution: In ΔABD and ΔACD:

AB = AC ( equal sides of an isosceles triangle)

∠ABD = ∠ADC (AD is the altitude)

AD = AD (common)

By RHS rule, ΔABD ≅ ΔACD, By cpct BD = CD or AD bisects BC

Also by cpct ∠BAD = ∠CAD or AD bisects A.

Conclusion

This chapter on triangles explores the various properties, theorems, and applications related to congruence and inequalities within triangles. Understanding these principles is fundamental to solving geometric problems and proving the relationships between different elements of triangles.

Class 9 Math Chapter 7 – Triangles offers a comprehensive understanding of the various properties, theorems, and criteria related to triangles. Mastering the concepts of congruence, such as SAS, ASA, and RHS, as well as understanding the properties of isosceles and equilateral triangles, provides a solid foundation for geometric problem-solving. By exploring these topics through the engaging learning resources provided by iPrep, students can grasp the complexities of Triangles with ease and confidence. So, dive into the world of triangles and reinforce your understanding of Class 9 Math Chapter 7 – Triangles. With iPrep, learning becomes both effective and enjoyable, ensuring you excel in mastering the concepts of triangles.

Remember, Class 9 Math Chapter 7 – Triangles is crucial for building your geometry skills. So, keep practicing and strengthening your grasp on this important chapter!