Circles – Complete Guide For Class 10 Math Chapter 10

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Circles in Mathematics for Class 10th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples. 

The chapter on Circles explores the geometric properties of circles and their tangents. It begins by introducing fundamental elements such as the radius, diameter, chord, and arc. The concept of a tangent to a circle is then explained, emphasizing that a tangent touches the circle at exactly one point and that the radius at this point is perpendicular to the tangent.

The chapter also discusses the number of tangents that can be drawn from a point to a circle, noting that two tangents can be drawn from a point outside the circle, and one from a point on the circle. Understanding these concepts equips students with the skills needed to solve problems related to circles, tangents, and chords, enhancing their geometric reasoning and problem-solving abilities.

Circles

Imagine a bicycle moving along a road. If we consider the road as a straight line, it touches both wheels of the bicycle at only one point. This simple scenario introduces us to an essential geometric concept: the tangent of a circle.

In mathematical terms, a tangent to a circle is a line that touches the circle at exactly one point. This unique interaction forms the basis for understanding the geometric properties of circles and their tangents.

Understanding the Relationship Between a Circle and a Line

Consider a circle with center O and a line AB in a plane. The orientation of the line relative to the circle can create three different scenarios:

1. Non-intersecting Line: When the line AB does not intersect the circle at any point, it is known as a non-intersecting line concerning the circle.

2. Secant Line: If the line AB touches the circle at two distinct points, say P and Q, it is termed as a secant line of the circle.

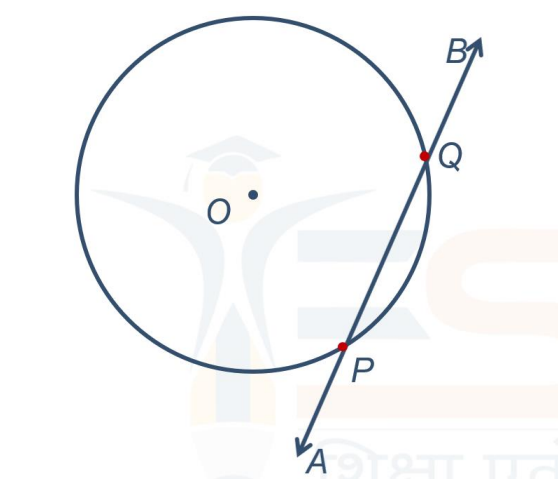
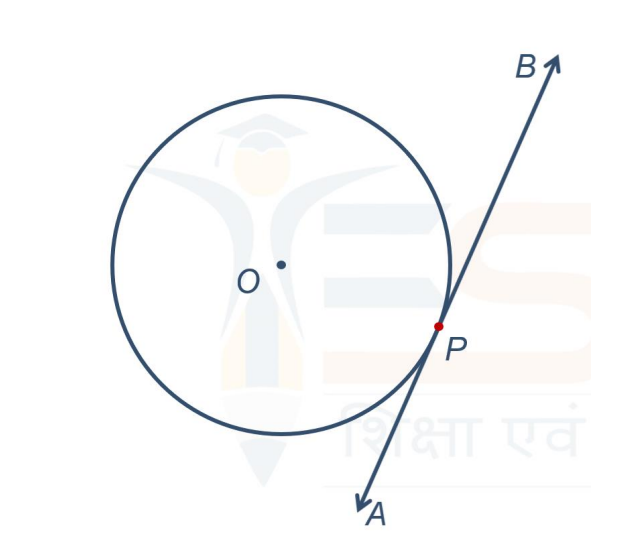
3. Tangent Line: When line AB touches the circle at only one point, P, it is referred to as a tangent line of the circle.

Tangent to a Circle

A tangent is defined as a line that touches a circle at exactly one point. This point is known as the point of contact.

Characteristics of Tangents

Let’s delve deeper into the properties of tangents with the help of a few illustrations:

• Consider a circle with center O and a secant line PQ. If we rotate PQ around the circle, keeping point P fixed, the length of the chord PQ decreases until it eventually reduces to zero, at which point Q coincides with P. This position gives us the tangent AB, with P as the point of contact.

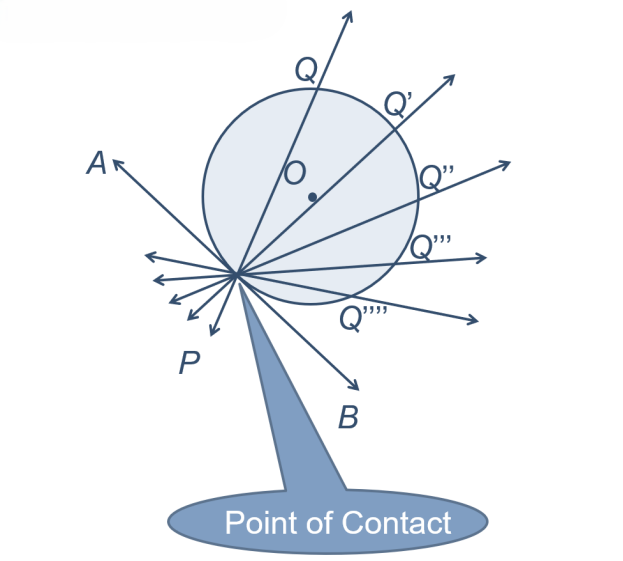
• Continuing the rotation of PQ beyond this point causes the chord to increase in length, but the tangent remains a unique case where only one tangent can be drawn from a point on the circumference of the circle.

The Tangent-Radius Relationship

Another significant property of tangents is their relationship with the radius of the circle:

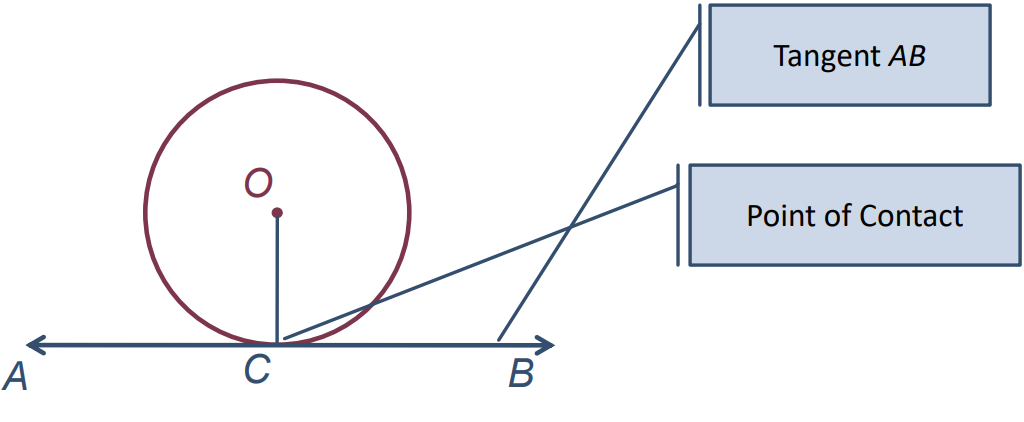
• Given a circle with center O and a tangent AB at point C, the radius OC drawn to the point of contact is always perpendicular to the tangent.
• This perpendicularity holds for any point P on line AB, meaning the radius drawn through the point of contact is the shortest distance between the center O and the tangent.

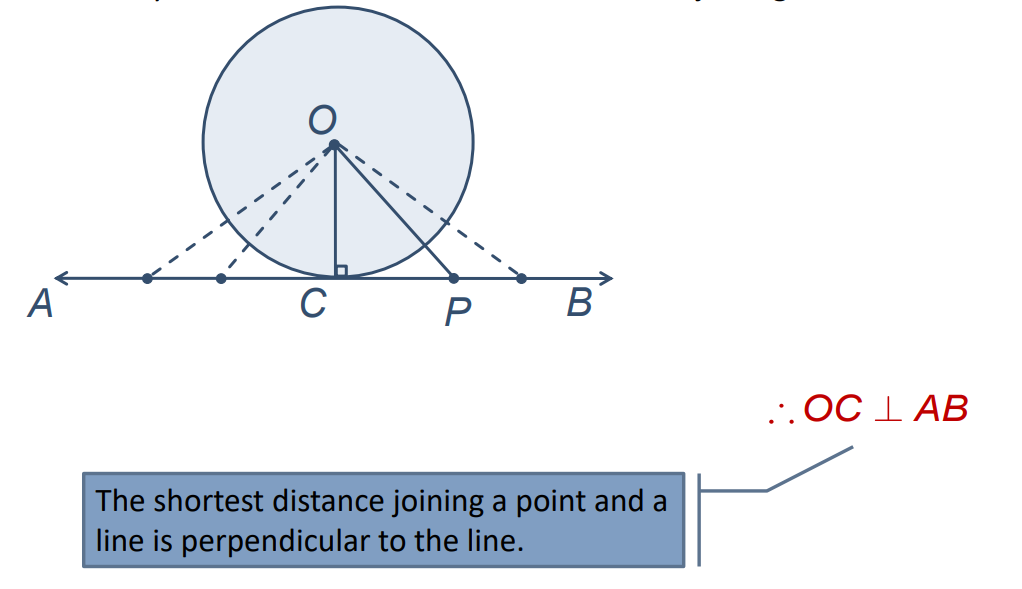
The observations above can be summarized in a key geometric theorem:

The Tangent Theorem: The tangent at any point of a circle is perpendicular to the radius through the point of contact.

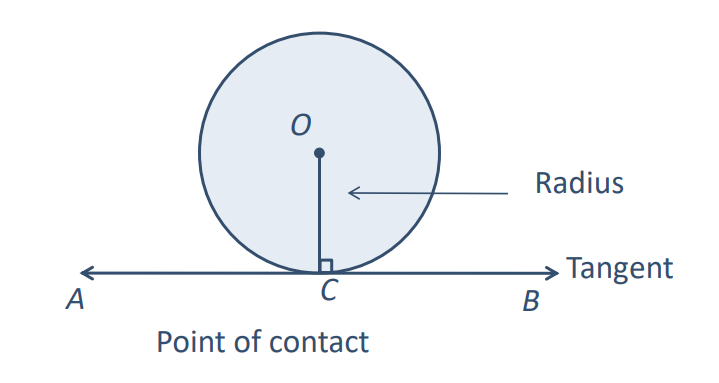
In the diagram, if OC is the radius and AB is the tangent at point C, then ∠OCB = ∠OCA = 90⁰

Conclusion

• The line containing the radius through the point of contact is called the ‘normal’ to the circle at the point. 
• A circle can have an infinite number of tangents, but at any point on a circle, there can be one and only one tangent.

Example: 

A point P is 17 cm from the center of a circle whose radius is 8 cm. Find the length of the tangent drawn to the circle at C from point P.

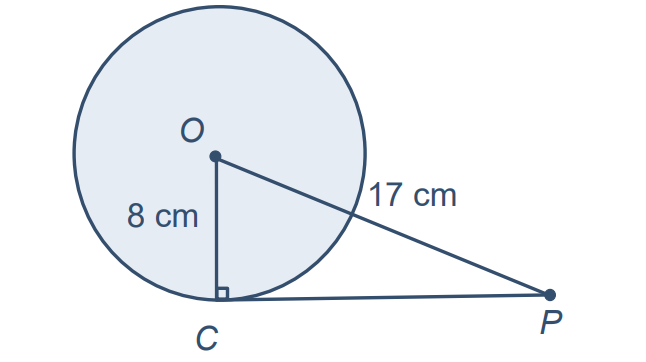
Let the length of the tangent CP = x cm.

OC = radius = 8 cm

OP = 17 cm. OC⟂OP (Radius is perpendicular to the tangent at the point of contact)

∆OCP is a right-angle triangle, right-angled at C.

Using Pythagoras Theorem, we have

OP² = OC² + CP²

17² = 8² +x² ⇒ x² = 17² – 8² = 289 – 64 = 225

⇒ x = 15 cm

Number of Tangents from a Point

The number of tangents that can be drawn to a circle depends on the position of the point relative to the circle:

1. When the point lies inside the Circle: No tangent can be drawn from a point inside a circle.

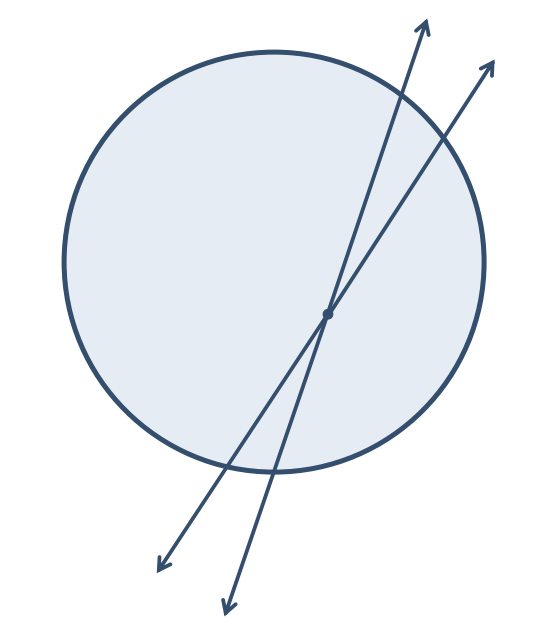
2. When the point lies on the Circle: Only one tangent can be drawn from a point on the circle.

3. When the point lies outside the Circle: Two tangents can be drawn from a point outside the circle.

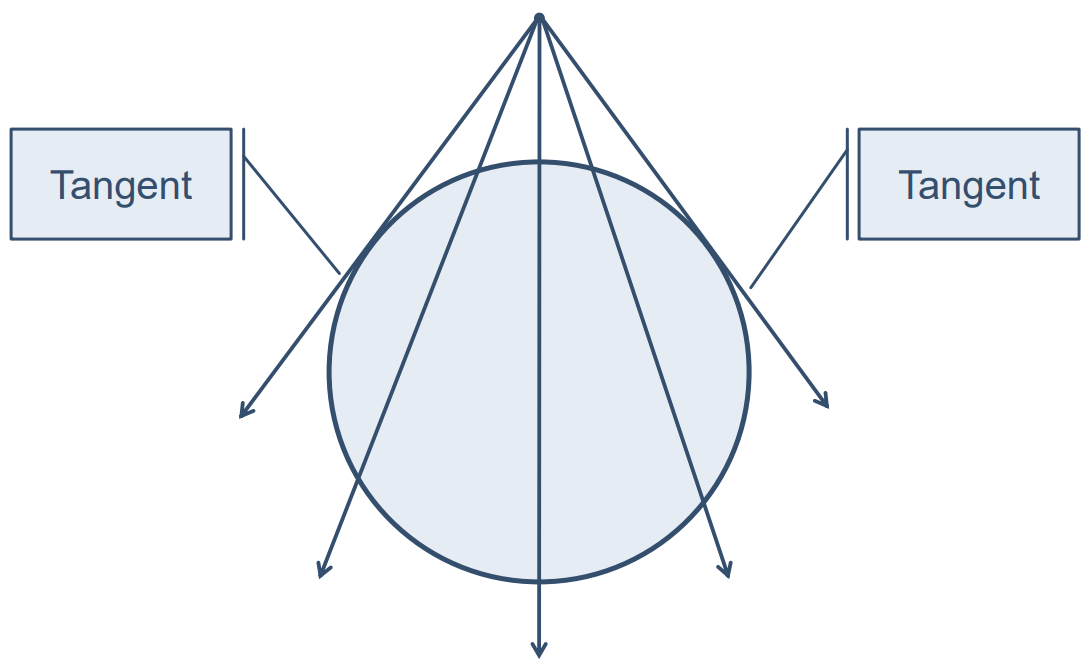
Equal Lengths of Tangents from an External Point

A remarkable property of tangents is that the lengths of the tangents drawn from an external point to a circle are equal.

Consider a circle with a center O and a point P outside the circle. The tangents PA and PB drawn from P to the circle are of equal length.

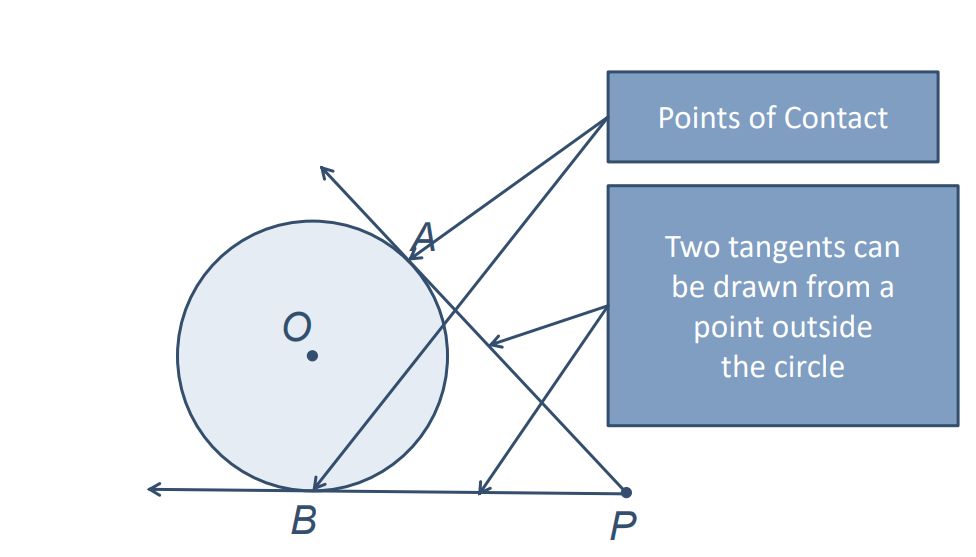
Let’s understand this:

A circle with center O and two tangents PA and PB to the circle are given.

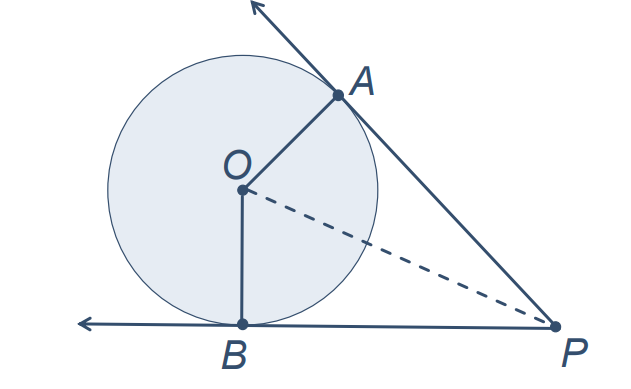
Join OA, OB, and OP.

In ∆OAP and ∆OBP, ∠OAP = ∠OBP = 90⁰

OP = OP (Common)

OA = OB (radii of the same circle)

∆OAP ≅ ∆OBP (RHS Congruence Criterion)

Therefore PA = PB (by CPCT)

This observation leads us to another geometric theorem:

The Tangent Length Theorem

The lengths of tangents drawn from an external point to a circle are equal.

In the diagram, if PA and PB are the tangents, then PA = PB

∠APO = ∠BPO (by CPCT) i.e.OP bisects ∠APB

Therefore, the center O lies on the bisector of the angle between the two tangents.

Example:

In the given figure, ∠AOB = 50⁰. Find ∠ABO and ∠OBT

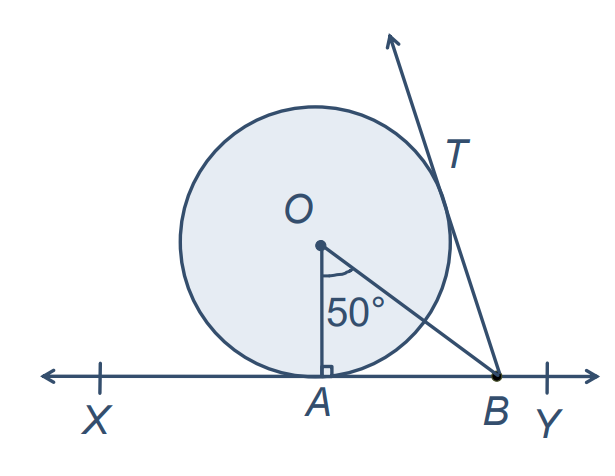
We know that OA ⟂  XY (As the radius is perpendicular to the tangent at the point of contact)

Therefore, ∠OAB = 90⁰

In ∆OAB, ∠OAB +∠ABO +∠AOB = 180⁰ (Using the angle sum property of a triangle)

∠ABO = 180⁰ – (90⁰+ 50⁰)

⇒ ∠ABO = 40⁰

∠ABO = ∠OBT = 40⁰

Let’s Conclude

In conclusion, CBSE Class 10th Math, Chapter 10 – Circles is a foundational topic that enhances students’ understanding of geometric properties related to circles and tangents. From the definition of a tangent to the exploration of the tangent-radius relationship, this chapter equips students with vital knowledge and problem-solving skills. Understanding the key theorems, such as the Tangent Theorem and the Tangent Length Theorem, is crucial for solving complex geometric problems. With our comprehensive resources on iPrep, mastering the concepts in Chapter 10 – Circles becomes an engaging and enriching experience. Whether it’s through animated videos, practice questions, or notes, you can deepen your understanding of Circles and excel in your studies.