Complete Guide For Class 10 Math Chapter 14 – Probability

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Probability in Mathematics for Class 10th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples. 

The chapter Probability in Class 10th Math introduces students to the concept of chance and the likelihood of events occurring. It covers the foundational ideas of random experiments, sample space, and events. Students learn to calculate the probability of an event using the ratio of favorable outcomes to the total number of outcomes. The chapter also explores types of events, including impossible, sure, and complementary events, and distinguishes between theoretical and experimental probability. Mastery of these concepts is crucial for understanding uncertainty and making predictions based on probability.

Introduction to Probability

Probability deals with the uncertainty associated with various events. It is a mathematical tool used to assign a numerical value to the degree of uncertainty. Whether it’s predicting the weather, tossing a coin, or drawing a card from a deck, probability plays a crucial role in various fields, including science and engineering.

There are two main types of probability:

• Experimental Probability: Based on actual experiments and events that have already occurred.
• Theoretical Probability: Predicts the likelihood of an event happening without actually experimenting.

Basic Definitions in Probability

Consider a random experiment of tossing two coins simultaneously 

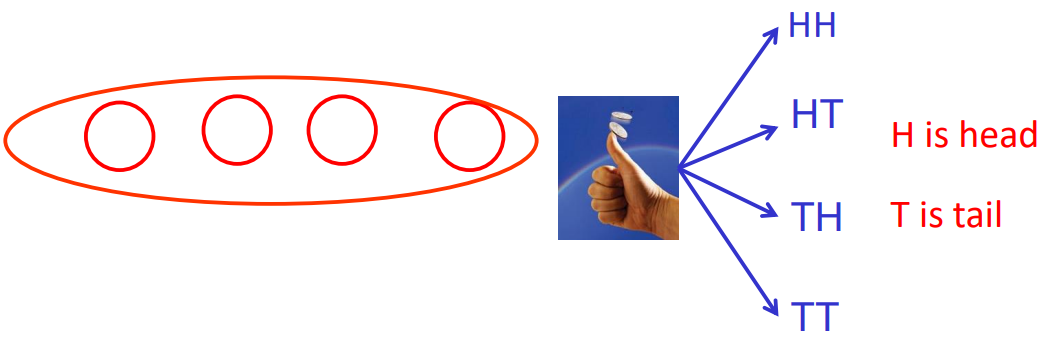
1. Compound Event: This is an event formed by combining two or more elementary events related to a random experiment.
2. Elementary Events: These are the most basic outcomes of a random experiment. For instance, in tossing two coins simultaneously, the possible elementary events are TT, TH, HT, and HH.

             Example: Let us take an example of throwing a die.

             Event: Throwing a die is an Event.

             Elementary Event: The outcomes are one, two, three, four, five, and six.

                  1, 2, 3, 4, 5, and 6 are the outcomes.

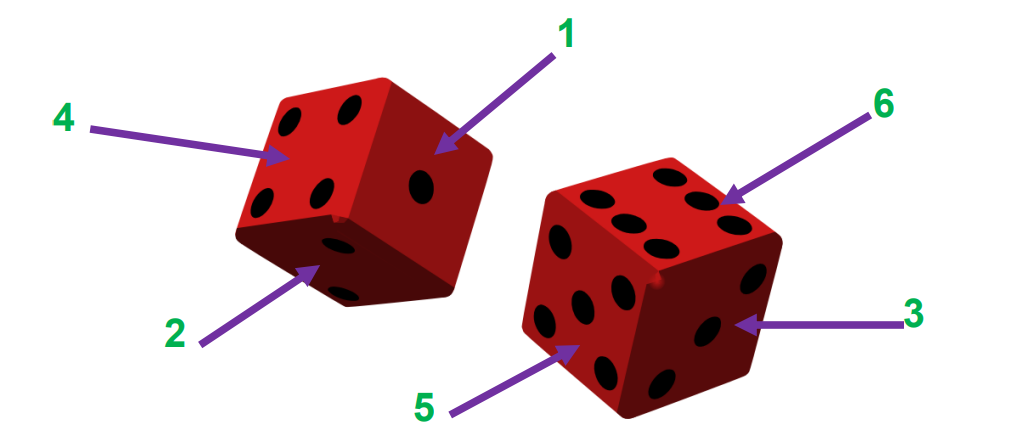
Example: Let us define an event E, i.e., E = Getting an odd number. 

Elementary events are 1, 2, 3, 4, 5, 6. 

If we get the outcome associated with the given event (1, 3, 5), then it is said that event E occurred.

3. Occurrence of an Event: An event is said to occur if any of the elementary events related to it is the outcome. For example, if you define an event E as getting an odd number when rolling a die, and you roll a 3, then event E has occurred.

If we get outcomes that are not associated with the given event (1, 3, 5), then it is said that event E does not occur. 

4. Favorable Elementary Event: An elementary event that satisfies the condition of a compound event is called a favorable elementary event. For example, if the event is “getting an odd number” when rolling a die, then 1, 3, and 5 are favorable elementary events.

Example: The event is “getting an odd number”. 

Favorable Elementary Event: (1, 3, 5)

5. Negation of an Event: The negation of an event A is defined as the event “not A,” which occurs when event A does not happen. For instance, the negation of “getting an odd number” is “getting an even number.”

Negation of the event is “getting an even number”. 

Non-favorable event: (2, 4, 6)

Elementary Event: The outcomes are one, two, three, four, five and six. 

Let us define an event E, i.e., E = Getting a number multiple of 7. P(E) = 0 

It is impossible to get a number multiple of 7.

6. Impossible Event: An event that cannot occur has a probability of 0 and is called an impossible event. For instance, getting a multiple of 7 when rolling a standard die is impossible.

Let us define an event E, i.e., E = Getting a number multiple of 1.

Elementary Event: The outcomes are one, two, three, four, five and six. Let us define an event E, i.e., E = Getting a number multiple of 1. P(E) = 1 It is always possible to get a number multiple of 1

7. Sure Event (Certain Event): An event that is certain to happen has a probability of 1. For example, getting a multiple of 1 when rolling a die is a sure event.

Key Probability Formula

The probability of an event E is calculated using the formula:

P(E) = Number of favorable outcomes / Total number of possible outcomes

Examples to Illustrate Probability

1. Candy Selection:
   • If a bag contains only orange-flavored candies, the probability of picking an orange candy is 1, while the probability of picking a lemon candy is 0.
2. Tossing Coins:
   • When two unbiased coins are tossed simultaneously, the probability of getting two heads (HH) is 1/4.
3. Throwing a Die:
   • If Gaurav throws a die, the probability of getting a real number less than 3 is 1/3, while the probability of getting a number equal to 5 is 1/6.
4. Drawing a Card:
   • From a pack of 52 cards, the probability of drawing a diamond is 1/4, while the probability of not drawing a diamond is 3/4. Similarly, the probability of drawing a black card is 1/2, and the probability of not drawing an ace is 12/13.

Key Points to Remember

1. The theoretical (classical) probability of an event E, written as P(E), is defined as P (E) = Number of outcomes favorable to E Number of all possible outcomes of the experiment where we assume that the outcomes of the experiment are equally likely. 

2. The probability of a sure event (or a certain event) is 1. 

3. The probability of an impossible event is 0. 

4. The probability of an event E is a number P(E) such that 0 ≤ P(E) ≤ 1 

5. An event having only one outcome is called an elementary event. The sum of the probabilities of all the elementary events of an experiment is 1. 

6. For any event E, P (E) + P ( E ) = 1, where E stands for ‘not E’. E and E are called complementary events.

Let’s Conclude

In summary, CBSE Class 10th Math, Chapter 14 – Probability provides essential insights into understanding and calculating the likelihood of various events. Mastery of this chapter is crucial for solving real-world problems that involve uncertainty and chance, whether in everyday life or more complex scientific and mathematical applications.

By engaging with the chapter Probability in Class 10th Math, students gain a solid foundation in key concepts such as experimental and theoretical probability, elementary and compound events, and the calculation of probabilities using basic formulas. Understanding these concepts helps in making informed predictions and decisions based on probability.

We at iPrep are dedicated to supporting your learning journey through interactive and comprehensive resources. Our animated videos, practice questions, and detailed notes are designed to make the study of Probability in Class 10th Math engaging and effective. Keep exploring these resources to build a robust understanding of probability and excel in your mathematics curriculum.