Introduction to Trigonometry – Awesome Guide For Class 10 Math Chapter 8

Struggling with Trigonometry? Master it with iPrep’s engaging videos, practice questions, and notes—designed to make learning easy and fun!

The chapter Introduction to Trigonometry introduces students to the fundamental concepts of trigonometry, focusing on the relationships between the angles and sides of a right-angled triangle. Students learn about trigonometric ratios—sine, cosine, and tangent—and how these ratios are used to solve problems involving right-angled triangles. The chapter covers the calculation of trigonometric ratios for specific angles such as 0°, 30°, 45°, 60°, and 90°, and explores their applications. Additionally, students are introduced to the concept of complementary angles and basic trigonometric identities.
Keep going and unlock the secrets of triangles and boost your math confidence! With iPrep, you’ll learn Trigonometry faster and easier than ever before.

Introduction to Trigonometry

Imagine you’re on an airplane flying at a certain height. You notice two towns directly to the left of the plane. How would you calculate the distance between these two towns? The answer lies in the fascinating field of trigonometry.

The word “Trigonometry” is derived from the Greek words:

1. Trigonon – meaning a triangle.
2. Metron – meaning to measure.

The word Trigonon means a triangle and the word Metron means to measure. Hence, trigonometry means the science of measuring triangles. Trigonometry literally means ‘measuring triangles’—but it does so much more! From GPS systems to roller coaster designs, introduction to trigonometry is everywhere.

Understanding Trigonometry

Angle

An angle is formed when a ray rotates around its endpoint. The initial position of the ray is called the initial side, and the final position after rotation is called the terminal side. The point around which the ray rotates is known as the vertex of the angle.

Measurement of an Angle

The measurement of an angle is determined by the amount of rotation from the initial side to the terminal side. Trigonometry is deeply rooted in the measurement of angles, with the most common unit being degrees.

Trigonometric Ratios

In a right-angled triangle, trigonometric ratios express the relationship between an acute angle and the lengths of the sides of the triangle. These ratios are essential for understanding the properties of triangles.

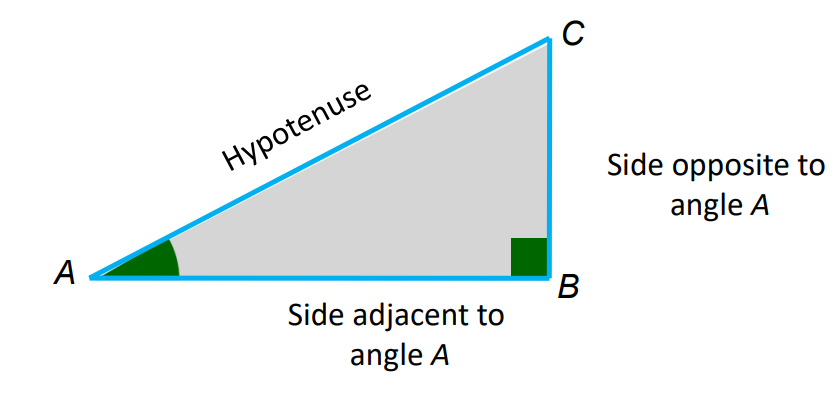
In a right-angled triangle ABC:

• Adjacent side (AB): The side next to the angle.
• Opposite side (BC): The side opposite the angle.
• Hypotenuse (AC): The side opposite the right angle, the longest side of the triangle.

Let’s move ahead with our journey of introduction to trigonometry and study the six trigonometric ratios.

Six Trigonometric Ratios

1. Sine (sin): The first basic trigonometric function is called sine (sin for short) and is defined as the ratio of the opposite side to the hypotenuse.

The ratio of the opposite side to the hypotenuse = BC / AC
         

              sin ⁡θ = Opposite side / Hypotenuse

2. Cosine (cos): The second basic trigonometric function is called cosine (cos for short) and is defined as the ratio of the adjacent side to the hypotenuse

             The ratio of the adjacent side to the hypotenuse = AB / AC
            

              cos ⁡θ = Adjacent side / Hypotenuse​

3. Tangent (tan): The third basic trigonometric function is called tangent (tan for short) and is defined as the ratio of the opposite side to the adjacent side.

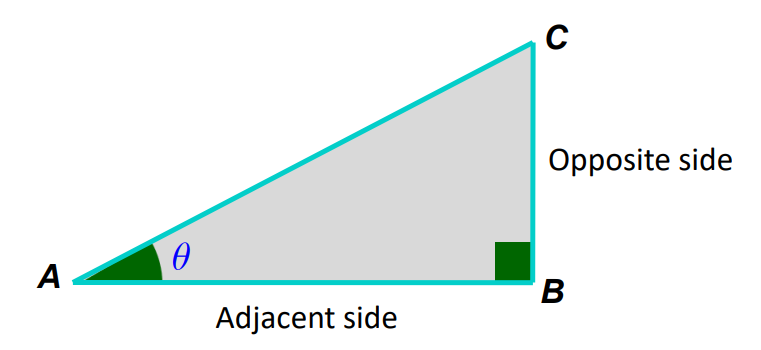
The ratio of the opposite side to the adjacent side = BC / AB

              tan⁡ θ = Opposite side / Adjacent side​

The other three ratios are the reciprocals of the above:

4. Cotangent (cot): Contangent of ∠⁡θ = Adjacent side / Opposite side = AB / BC, 

It is the reciprocal of tan.  

Cot⁡ θ = 1 / tan ⁡θ​

5. Secant (sec): Secant of ∠⁡θ = Hypotenuse / Adjacent side = AC / AB  

             It is the reciprocal of cos. 

             sec ⁡θ = 1 / cos⁡ θ​

6. Cosecant (cosec): Cosecant of ∠⁡θ = Hypotenuse / Opposite side = AC / BC

                It is the reciprocal of sin.

                cosec ⁡θ = 1 / sin ⁡θ

Reciprocal of Trigonometric Ratios

These reciprocal relationships form the basis of more complex trigonometric calculations, linking the fundamental trigonometric functions.

 cot⁡ θ = 1 / tan ⁡θ​

             sec ⁡θ = 1 / cos⁡ θ​

             cosec ⁡θ = 1 / sin ⁡θ

Relationship Between Sine, Cosine, and Tangent

In a right-angled triangle, the trigonometric ratio tan θ can be expressed in terms of sin θ and cos θ:

                tan θ = cos θ / sin θ​

Let’s move ahead with introduction to trigonometry and learn how to calculate trigonometric ratios of specific angles.

Trigonometric Ratios of Specific Angles

Using a trigonometric table, you can find the trigonometric ratios of specific angles like 0°, 30°, 45°, 60°, and 90°.

Trigonometric Ratios of 45°

In a right-angled triangle ABC:

Let BC = AC = x. By Pythagoras’ Theorem, we have

AC = √AB² + BC² = √x² + x² = x /√2

Therefore, sin 45° = BC / AC = x/ x /√2 = 1/√2

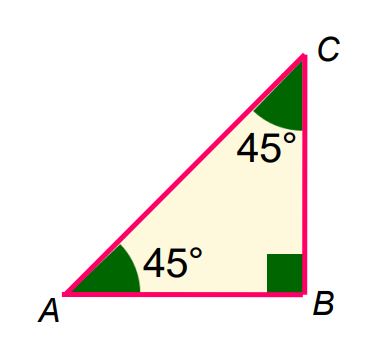
In the same way, other ratios are

• cos⁡ 45°= 1/√2​
• tan ⁡45°= 1
• cosec 45° = √2​
• sec 45° = √2​
• cot 45° = 1​

Trigonometric Ratios of 30° and 60°

In a triangle with specific angle measurements:

Let AB = BC = CA = 2x ⇒BD = 1/2 BC = x

In the right-angled triangle ABD,

By Pythagoras Theorem, we have

AD = √AB² – BD² = √2x² – x² = x /√3.

Therefore, sin 30° = BD /AB = x /2x = 1/2

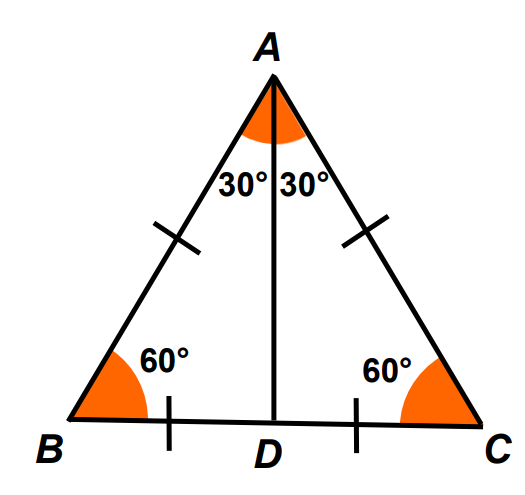
Similarly, the other ratios are:

• cos ⁡30°= √3/2​​
• tan ⁡30°= 1/√3​​
• cosec ⁡30°= 2​​
• sec ⁡30°= 2​​/√3
• cot ⁡30°= √3

Similarly, sin⁡ 60°= AD /AB = x √3/ 2x = ​​√3/2

• cos⁡ 60°= 1/2​
• tan⁡ 60°= √3
• cosec⁡ 60°= 2/√3​
• sec⁡ 60°= 2​
• cot⁡ 60°= 1/√3

Trigonometric Ratios of 0° and 90°

As angle A decreases to 0° or increases to 90° in a right-angled triangle, the trigonometric ratios adjust accordingly:

In ∆ABC, right-angled at B: If we continuously decrease the value of angle A, side BC also decreases. The point C coincides with point B when angle A becomes equal to zero. At this time AC will also be equal to AB.

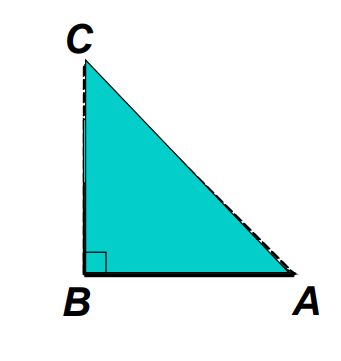
Here, sin θ = BC / AC is very close to zero 

i.e.sin 0° = 0

Since AC is nearly the same as AB, therefore cos θ = AB /BC is very close to 1 

i.e.cos 0° = 1 and tan 0° = sin 0° /cos 0° = 0 

Also cosec 0° = undefined, sec 0° = 1, and cot 0° = undefined

Similarly,  we have 

• sin ⁡90°= 1, cos⁡ 90° = 0, tan⁡ 90°= undefined, cos⁡ec 90°= 1, sec⁡ 90°= undefined, and cot 90° = 0

Trigonometric Table

A standard trigonometric table helps in finding the values of the sine, cosine, tangent, cosecant, secant, and cotangent for specific angles.

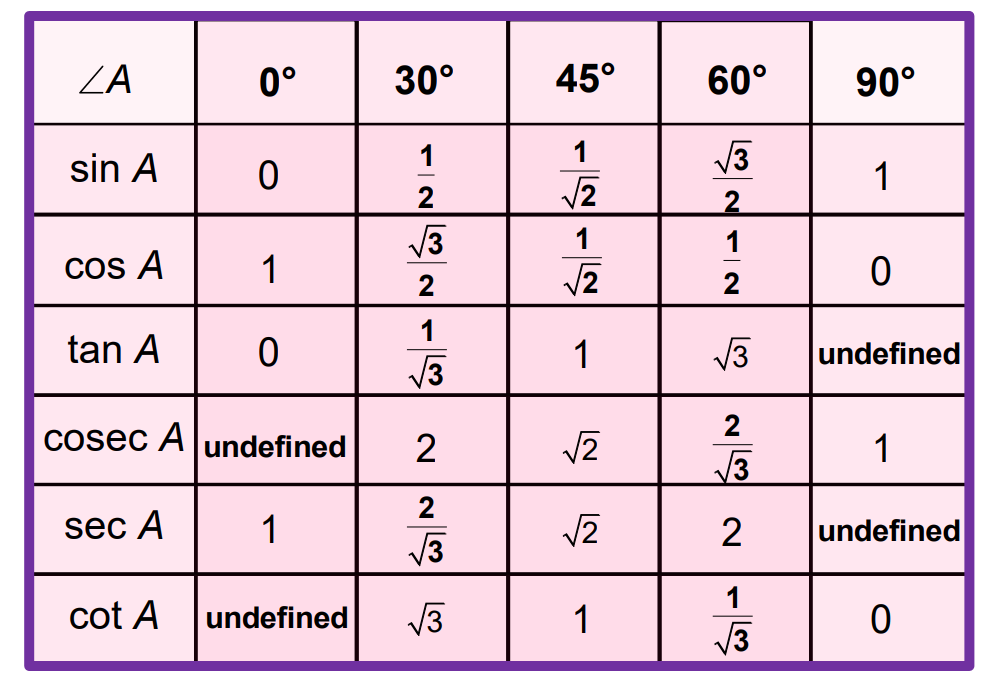
Example: Evaluate 2 cos⁡²45°

Using the trigonometric table:

            2 cos⁡²45°= 2 x (1/√2)⁡² = 1

Complementary Angles

Two angles are said to be complementary if their sum equals 90°. In a right-angled triangle, the two acute angles are complementary.

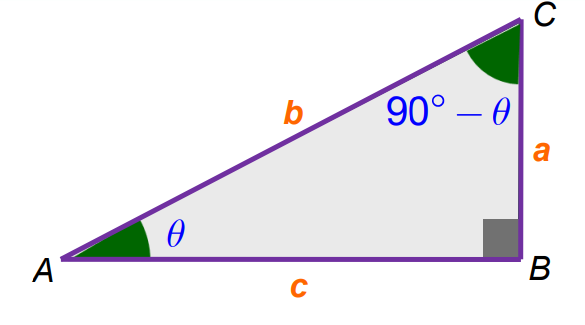
In a right-angled ∆ABC, the two acute angles are complementary

Thus, if one acute angle of a right-angled triangle is θ, then the other is (90° – θ)

Therefore if sin θ = a/b, then cos (90° -θ) = a/b

Thus we get, sin ⁡θ = cos ⁡(90°−θ)

Similarly,  In ∆ABC, the trigonometric ratio of complementary angle (90°−θ) is given by 

• cos ⁡(90°−θ) = sin θ
• tan ⁡(90°−θ) = cot θ
• cot ⁡(90°−θ) = tan θ
• cosec ⁡(90°−θ) = sec θ
• sec ⁡(90°−θ) = cosec θ 

Trigonometric Identities

A trigonometric identity is an equation that holds true for all values of the variables involved. Here are some basic trigonometric identities:

            sin²A + cos²A = 1

1 + tan⁡²A = sec⁡²A

1 + cot⁡²A = cosec⁡²A

Example: Prove that sin⁡x / cos⁡x = tan⁡x

Proof: we know that 

sin⁡x / cos⁡x = tan⁡x

This equation is true for all values of x, making it a valid trigonometric identity.

Let’s Conclude

In conclusion, CBSE Class 10th Math, Chapter 8 – Introduction to Trigonometry provides a comprehensive foundation in trigonometry, a vital branch of mathematics. 

 🚀 Ready to ace Trigonometry? Watch our engaging videos and practice with real exam questions on iPrep. Click to start learning now! Embrace the challenges of Introduction to Trigonometry, and let this chapter serve as a stepping stone to more advanced mathematical learning.