Integers – Complete Guide For Class 7 Math Chapter 1

Welcome to iPrep, your Learning Super App.  Our learning resources for the chapter, Integers in Mathematics for Class 7th are designed to ensure you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples. 

The chapter on Integers is designed to build a strong foundational understanding of integers, their properties, and operations. Integers are a critical concept in mathematics, forming the basis for more complex topics and applications. This chapter aims to introduce students to integers, their representation, and operations, ensuring they grasp the fundamental principles required for higher-level math.

Basic Definitions

• Integers – The set of all whole numbers along with the numbers –1, -2, -3,…..is called the set of integers i.e …,-4, -3, -2, -1, 0, 1, 2, 3, 4,… 

Types of Integers

1. Negative integers: -4, -3, -2, -1
2. Positive integers: 1, 2, 3, 4

Characteristics

1. They are like whole numbers but include negative numbers.
2. Integers can be zero, negative, or positive.

Example of Subtraction Patterns

Let’s observe the Pattern: 

• 4 – 1 = 3
• 4 – 2 = 2
• 4 – 3 = 1
• 4 – 4 = 0
• 4 – 5 = -1 (This is a negative number).

A negative number is always less than zero.

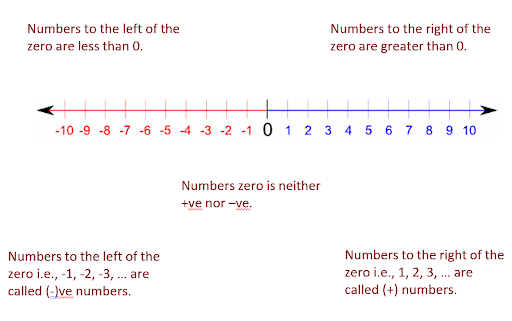
Representation of Integers on the Number Line

• Negative Numbers: Represented by (-) sign.
• Positive Numbers: Represented by (+) sign.

Key Points Of Representing Integers on the Number Line

There are several points to be considered when representing Integers on the number line. Those include:

• All points marked on the number line should be at equal distances from each other.
• 0 is in between the positive and negative integers.
• Numbers to the left of zero are less than 0.
• Numbers to the right of zero are greater than 0.
• Zero is neither positive nor negative.

A few examples of placing integers on the number line

• To represent 4 on the number line: Move 4 points to the right of 0.
• To represent -4 on the number line: Move 4 points to the left of 0.

Ordering of Integers

• Lesser Values: The value decreases as you move to the left on a number line.
• Greater Values: The value increases as you move to the right on a number line.

Now that we understand the ordering of the integers, let’s understand the Addition and Subtraction rules of the Integers

Addition and Subtraction Rules of the Integers

Addition of Integers 

Rules for the Addition of Integers include:

• Positive + Positive = Positive
• Positive + Negative = Depends on the absolute values
• Negative + Negative = Negative

Examples:

• 5 + 3 = 8
• -2 + 5 = 3
• -3 + (-4) = -7

Addition of Integers on the Number Line

Subtraction of Integers

Rules for the Subtraction of Integers include:

• Positive – Positive = Depends on the values
• Positive – Negative = Positive
• Negative – Positive = Negative
• Negative – Negative = Depends on the absolute values

Examples:

• 5 – 3 = 2
• 7 – (-2) = 9
• -4 – 6 = -10
• -5 – (-3) = -2

Subtraction of Integers on the Number Line

Properties of Addition and Subtraction of Integers

Closure Under Adition

For any two integers a and b, 

a + b is an integer.

Examples: 

• 2+3 = 5
• (-8) + 4 = – 4
• 5 + (-4) = 1  

Closure Under Subtraction

For any two integers a and b,  a – b is an integer.

Examples: 

• 4 – 5 = -1
• (-4) – (-6) = 2 
• (-8) – 4 = -12

Commutative Property

For any two integers a and b, a + b = b + a

Examples: 

• 2 + 5 = 5 + 2 = 7
• (-4) + 5 = 5 + (-4) = 1

Associative Property

For any three integers a, b, and c, a + (b + c) = (a + b) + c

Examples: 

• -3 + [9 + (-7)] = -1 
• [(-3) + 9] + (-7) = -1

Additive Identity:

For any integer a, a + 0 = 0 + a = a

Examples: 

• (-5) + 0 = -5
•  3 + 0 = 3
•  0 + 7 = 7

Hence, 0 is called the additive identity. 

Now let’s learn about the Multiplication of Integers and Division of Integers:

Multiplication of Integers

1. Multiplication of Two Positive Integers
2. Multiplication of Two Negative Integers
3. Multiplication of Positive and Negative Integers

Key Points:

• Positive x Positive = Positive:

Example: 2 x 4 = 8

• Negative x Negative = Positive:

Example: (-4) x (-3) = 12

• Positive x Negative = Negative:

Example: 3 x (-4) = -12

Product of Three or More Negative Integers:

• Even the number of negative integers = Positive product
• Odd number of negative integers = Negative product

Example: (-3) x 2 x (-4) = 24

Now Let’s understand the Properties of Multiplication

Closure Under Multiplication:

For all integers a and b, 

a x b is an integer

Examples: 

• 5 x (-3) = -15
• (-7) x (-6) = 42

Commutative Property

For any two integers a and b, 

a x b = b x a

Examples: 

• 2 x (-3) = (-3) x 2 = -6 
• (-6) x (-4) = (-4) x (-6) = 24

Multiplication by Zero

For any integer a, 

a x 0 = 0

Examples: 

• 5 x 0 = 0 
• (-7) x 0 = 0

• Multiplicative Identity:

For any integer a,

 a x 1 = a

Examples: 

• 1 x (-5) = -5 
• 1 x 3 = 3

• Associative Property:

            For any three integers a, b, and c, 

            (a x b) x c = a x (b x c)

            Example:

             [7 × (– 6)] × 4 = 7 × [(– 6) × 4] 

                       -42 x 4 = 7 x -24

                          -168 = -168

• Distributive Property:

           For any integers a, b, and c, 

            a x (b + c) = (a x b) + (a x c)

            Example:

                  (– 8) × [(–2) + (–1)] = [(– 8) × (–2)] + [(– 8) × (–1)]

                             (– 8) × (–3)  = 16 + 8 

                                            24 = 24

Division of Integers

          Basic Rules 

• The division is the inverse of multiplication.
• a x b = c implies c ÷ a = b and c ÷ b = a

For any Two Positive Integers:

• a ÷ (-b) = (-a) ÷ b
• (-a) ÷ (-b) = a ÷ b, where b≠0

Examples:

• 10 ÷ (-2) = -5
• 14 ÷ (-7) = -2

Thus, by dividing a positive integer by a negative integer, the answer is a negative integer.

• (-6) ÷ (-2) = 3
• (-15) ÷ (-3) = 5

Thus, by dividing a negative integer by a negative integer, the answer is a positive integer.

Properties of Division

• Closure Under Addition: 

          Examples:

• (-10) ÷ 5 = -2 (integer)

• 8 ÷ 2 = 4 (integer)
• (-7) ÷ 3 = -7/3 (not an integer)

Thus, Integers are not closed under the Division

• Commutative Property:

Examples 

• 6 ÷ 3 = 2 and 3 ÷ 6 = 1/2 (not equal)

• Division by Zero:
•  a ÷ 0 is not defined.
• 0 ÷ a = 0 for a ≠ 0

Examples: 

• 2 ÷ 0 (not defined)
• 0 ÷ 4 = 0

Complex Cases:

Case 1 – The division of an integer by zero is not defined.

• 2 ÷ 0 = 0 (An integer cannot be divided by the number zero).

Case 2 – Zero divided by an integer other than zero is always equal to zero.

• 0 ÷ 4 = 0 (when the number zero is divided by any integer the result will be zero).

Case 3 – Zero divided by Zero is always equal to zero.

• 0 ÷ 0 = 0 (special case, often considered undefined in higher math)

• Division Identity

                 For any integer a, 

                   a ÷1 = a

• Associative Property:

               For any integers a, b and c,

                    (a ÷ b) ÷ c ≠ a ÷ (b÷ c)

The division is not associative.

Example: 

• (8 ÷ 2) ÷ 2 ≠ 8 ÷ (2 ÷ 2)

This summarizes the Class 7th Math Chapter 1 Integers entirely. For more such content together with practice questions, assessments, simulations, notes, and more, download the iPrep app now.