Perimeter and Area- Complete Guide For Class 7 Math Chapter 9

Welcome to iPrep, your Learning Super App. Our learning resources for the chapter, Perimeter and Area in Mathematics for Class 7th are designed to ensure that you grasp this concept with clarity and perfection. Whether you’re studying for an upcoming exam or strengthening your concepts, our engaging animated videos, practice questions and notes offer you the best of integrated learning with interesting explanations and examples. 

The chapter on Perimeter and Area aims to build students’ understanding of measuring the boundary and space of two-dimensional shapes. It introduces the concepts of perimeter and area, along with methods to calculate them for various geometrical figures. Learning about perimeter and area equips students with the skills to solve practical problems involving measurement and space, forming a fundamental part of their geometry education. By mastering the concepts of perimeter and area, students develop the ability to address real-world problems such as determining the amount of fencing required for a garden, the paint needed for a wall, etc, thereby laying a strong foundation for more advanced geometrical studies and applications.

Perimeter & Area

In the chapter perimeter and area various basic definitions are key to understanding the chapter thoroughly. These Include:

Basic Definitions:

Introduction to Perimeter

Perimeter is the distance around a given two-dimensional object.

It refers to the “around measure” of a flat shape.

Example: The perimeter of a pool is the outer boundary of the pool, obtained by adding up all its sides.

Introduction to Area

The chapter perimeter and area comes with a detailed introduction to the concept of area. It states that “Area” is a quantity expressing the two-dimensional size of a defined part of a surface, typically a region bounded by a closed curve.

Example: The area of a pool is shown as the shaded region, which includes the outer boundary of the pool and its interior.

Perimeter of a Regular Polygon

Perimeter = Number of sides × Length of each side

Example: For a pentagon with each side of length ‘a’ units, the perimeter will be 5×a units.

The Perimeter of a Square:

Perimeter = 4 × Length of each side

Example: For a square with each side of length ‘a’ units, the perimeter will be 

4 × a units.

Perimeter of a Rectangle

Perimeter = 2 × (Length+Breadth)

Example: For a rectangle with length ‘a’ units and breadth ‘b’ units, the perimeter will be 2×(a+b) units.

Key Points to find the Length and Breadth of a Rectangle if the Perimeter is given:

• If the measures of the perimeter of a rectangle & its breadth are given;

           Length of rectangle = Perimeter of Rectangle/2 – Breadth of rectangle

• If the measures of the perimeter of a rectangle & its length are given;

          The breadth of rectangle = Perimeter of Rectangle/2 – Length of rectangle

Example: The measure of the boundary of a square table top is 56 inches. Find the length of each side of the table.

          Length of each side = Perimeter/4 = 56/4 = 14 inches

Example: A tape is required to be pasted around a picture frame with a length of 15 cm and a breadth of 8 cm. Find the length of tape required to build the frame.

            Length of tape = 2 × (length + breadth) =2 × (15 + 8) = 2×23 = 46 cm

Area of a Square: (side)² = a²

For a square tile with each side ‘a’ units, the area will be a × a = a² square units.

Area of a Rectangle: length × breadth = l × b

For a rectangular field with length ‘l’ units and breadth ‘b’ units, the area will be l × b square units.

Key Points to find the Length and Breadth of a Rectangle if the Area is given:

• If the measures of the area of a rectangle and its breadth are given; 

           Length of rectangle = Area of Rectangle/ Breadth of rectangle

• If the measures of the area of a rectangle and its length are given;

           The breadth of rectangle = Area of Rectangle/ Length of rectangle

Example: The area of a whiteboard is equal to its perimeter. If its area is 1.35 m², find the perimeter if the length of the board is 1.5 m.

          Area = 1.5 × b 

          1.35 =  1.5 x b ⇒ b = 1.35 = 0.9 m

          Perimeter = 2 × (length + breadth) = 2 × (1.5 + 0.9) = 2 × 2.4 = 4.8 m

Triangles as Part of Rectangle

In the chapter Perimeter and Area, represents triangles as parts of rectangles. Here’s how

Cutting a Rectangle Along Its Diagonal: If we cut a rectangle along its diagonal, we get two congruent triangles, each with an area equal to half the area of the rectangle. Also, the sum of the areas of the two triangles is the same as the area of the rectangle from which they are cut.

Area of each triangle = 1/2  × (length × breadth) = 1/2 x (l x b)

Example: The length and breadth of a rectangle are 17 cm and 9 cm respectively. Find the area of the triangles formed by joining one of its diagonals.

Area of each triangle = 1/2 × (17 × 9) = 76.5 cm² 

Triangles as Part of Square

In the chapter Perimeter and Area, represents triangles as parts of squares as well. Here’s how

Cutting a Square Along Its Diagonal: If we cut a square along both its diagonal, we get four triangles. All these four triangles are congruent and hence equal in area. Also, the sum of the areas of the two triangles is the same as the area of the rectangle from which they are cut.

Area of each triangle = 1/4 x (Area of the square) = 1/4 x (side²)

Area of a Parallelogram

Formula: Area = base × height

Key Points: 

• The base can be any of the four sides of the parallelogram. 
• The height is perpendicular to the base.

Example: One of the sides and the corresponding height of a parallelogram are 11 cm and 6 cm respectively. Find the area of the parallelogram.

Area = 11 × 6 = 66 cm² 

Key Points to find out the Height and Base if  the Area of Parallelogram is given:

• If the measures of the area of a parallelogram & its base are given;

Height of parallelogram = Area of parallelogram / Base of Parallelogram

• If the measures of the area of a parallelogram & its height are given;

Base of parallelogram = Area of parallelogram / Height of Parallelogram

Area of a Triangle

The chapter perimeter and area also covers the concept of area of a triangle. This involves:

Cutting a Parallelogram Along Its Diagonal: If we cut a parallelogram along its diagonal, we get two congruent triangles, each with an area equal to half the area of the parallelogram.

Area of each triangle = 1/2 × (base × height)

Example: Find the area of the triangle shown in the figure. The altitude on side XY is 9 cm long.

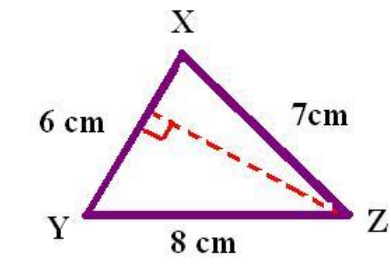
Area =  1/2 × (base × height) = 1/2 × (6 × 9) = 27 cm² 

Circles

Circumference of a Circle: Circumference is the distance around a circular region.

Circumference = π × diameter, where π≈3.14

Example: A circle was folded and cut from the center. Find the length of the boundary of the semi-circular disc so formed. (𝜋 = 22/7)

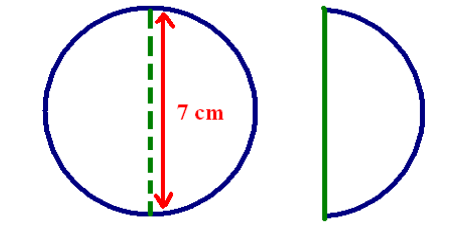
Length of the straight edge = diameter = 7 cm

Curved edge = 1/2  x Circumference of circle = 1/2  x 𝜋 x 7 = 1/2  x 22/7 x 7 = 11 cm

Total boundary = 11 + 7 = 18 cm

Area of a Circle: The measure of the region occupied by a circle is its area.

Area = π × r² 

Example: A silver coin needs to be polished. It has a radius of 2 cm. Find the cost of polishing 15 such coins at the rate of ₹ 4 per cm².

Solution: Area of one coin = π × r² =  3.14 × 2 x 2 = 12.56 cm²

Total area of a coin to be polished = 2 × 12.56 = 25.12 cm² 

Total area of 15 such coins = 15 × 25.12 = 376.8 cm².

Cost of polishing = 4 × 376.8 = ₹ 1507.20

In conclusion, mastering the concepts of perimeter and area in Class 7 Math Chapter 9 is crucial for building a solid foundation in geometry. This chapter equips students with the ability to measure the boundaries and spaces of various two-dimensional shapes, which is not only essential for academic success but also for solving real-world problems. By thoroughly understanding perimeter and area, students will be well-prepared to tackle more advanced geometrical concepts in the future. Make sure to explore all the resources available in the iPrep Learning Super App to reinforce your understanding of Perimeter and Area, and to excel in your mathematical journey.